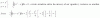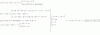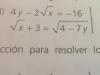-
Antonio Silvio Palmitano
el 4/3/18Tienes las ecuaciones cartesianas de las gráficas de las funciones: f(x) = x3 y g(x) = x, ambas con dominio R.
Comienza por plantear la condición de intersección entre las gráficas de las dos funciones, y para ello plantea el sistema de ecuaciones:
y = x3,
y = x;
luego, igualas expresiones, y queda:
x3 = x, haces pasaje de término, extraes factor común, y queda:
x*(x2 - 1) = 0, factorizas la expresión en el agrupamiento (observa que es una resta entre cuadrados perfectos), y queda:
x*(x + 1)*(x - 1) = 0, y observa que por anulación de un producto tienes tres opciones:
x = 0, que al evaluar en las expresiones de las funciones queda: y = 0,
x = -1, que al evaluar en las expresiones de las funciones queda: y = -1,
x = 1, que al evaluar en las expresiones de las funciones queda: y = 1,
por lo que tienes tres puntos de intersección:
A1(-1,-1), A2(0,0) y A3(1,1).
Luego, plantea los intervalos cuyos puntos de corte corresponden a los puntos de intersección, eliges un representante en cada intervalo y evalúas las expresiones de las funciones, a fin de determinar cuál de ellas toma valores mayores:
Ia = (-1,0), representado por x = -1/2, y para él tienes: f(x) = (-1/2)3 = -1/8 y g(-1/2) = -1/2, por lo que tienes que la función f toma valores mayores en este intervalo;
Ib = (0,1), representado por x = 1/2, y para él tienes: f(x) = (1/2)3 = 1/8 y g(1/2) = 1/2, por lo que tienes que la función g toma valores mayores en este intervalo.
Luego, plantea las expresiones de las áreas para los dos intervalos (recuerda que el argumento de la integral es la resta entre la expresión de la función que toma valores mayores, cuya gráfica es "más alta" y la expresión de función que toma valores menores, cuya gráfica es "más baja"):
Aa = -1∫0 ( f(x) - g(x) )*dx = sustituyes = -1∫0 (x3 - x)*dx = [ x4/4 - x2/2 ] = evalúas = (0 - 0) - (1/4 - 1/2) = -(-1/4) = 1/4,
Ab = 0∫1 ( g(x) - f(x) )*dx = sustituyes = 0∫1 (x - x3)*dx = [ x2/2 - x4/4 ] = evalúas = (1/2 - 1/4) - (0 - 0) = 1/4;
luego, tienes para el área total de la región limitada por las gráficas de las dos funciones:
A = Aa + Ab =1/4 + 1/4 = 1/2.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 4/3/18Plantea las expresiones de las funciones derivadas primera y segunda:
f ' (x) = 3a*x2 + 2b*x + c (1),
f ' ' (x) = 6a*x + 2b (2).
Luego, plantea la condición de recta tangente horizontal (observa que su pendiente es igual a cero) en el punto M(0,1):
f ' (0) = 0, sustituyes la expresión señalada (1) para x = 0 evaluada en el primer miembro, y queda: c = 0;
y como el punto de tangencia también pertenece a la gráfica de la función puedes plantear:
f(0) = 1, sustituyes la expresión de la función (que tienes en tu enunciado) evaluada en el primer miembro, y queda: d = 1.
Luego, plantea la condición de punto de inflexión en el punto Q(-1,3):
f ' ' (x) = 0, sustituyes la expresión señalada (2) evaluada para x = -1 en el primer miembro, y queda:
-6a + 2b = 0, aquí divides por 2 en todos los términos de la ecuación, haces pasaje de término, y queda: b = 3a (3);
y como el punto de inflexión también pertenece a la gráfica de la función puedes plantear:
f(-1) = 3, sustituyes la expresión de la función (que tienes en tu enunciado) evaluada en el primer miembro, y queda: -a + b - c + d = 3 (4).
Luego, reemplazas los valores remarcados y la expresión señalada (3) en la ecuación señalada (4), cancelas el término nulo, y queda:
-a + 3a + 1 = 3, haces pasaje de término, reduces términos semejantes, y queda:
2a = 2, haces pasaje de factor como divisor, y queda: a = 1;
luego, reemplazas este último valor remarcado en la ecuación señalada (3), resuelves, y queda: b = 3.
Luego, reemplazas los valores de los coeficientes que tienes remarcados en la expresión de la función, cancelas el término nulo y queda:
f(x) = x3 + 3x2 + 1.
Espero haberte ayudado.
-
Ángel
el 4/3/18Obtenemos el valor de x de la 1ª ecuación:
4y - 2√x = -16
2√x = 4y+6
√x = (4y+6)/2
elevamos al cuadrado ambos miembros:
(√x)2 = ((4y+6)/2)2
x = (4y+6)2/22
x = (16y2+62+2*4y*6)/4
x = (16y2+36+48y)/4
x = 4y2+12y+9
((si haces 4y2+12y+9=0 obtienes que las dos soluciones son -3/2)), entonces:
x = (2y+3)2
Sustituimos en la 2ª ecuación:
√((2y+3)2) +3 = √(4-7(2y+3)2)
2y+3+3 = √(4-7(2y+3)2)
Intenta continuar y nos mandas qué has sacado, te lo corregimos y completamos.
Antonio Silvio Palmitano
el 4/3/18Divides por dos en todos los términos de la primera ecuación, y el sistema queda:
2y - √(x) = -8 (1),
√(x) + 3 = √(4-7y) (2);
luego, sumas miembro a miembro entre ambas ecuaciones (observa que tienes cancelaciones en el primer miembro), y queda:
2y + 3 = -8 + √(4-7y), haces pasaje de término, reduces términos semejantes, y queda:
2y + 11 = √(4-7y), haces pasaje de raíz como potencia, y queda:
(2y + 11)2 = 4 - 7y, desarrollas el binomio elevado al cuadrado en el primer miembro, y queda:
4y2 + 44y + 121 = 4 - 7y, haces pasajes de términos, reduces términos semejantes, y queda:
4y2 + 51y + 117 = 0,
que es una ecuación polinómica cuadrática cuyas soluciones son:
a)
y = (-51 - 27)/8 = -39/4 = -9,75;
luego, reemplazas en la ecuación señalada (2), resuelves, y queda:
√(x) + 3 = 8,5, haces pasaje de término, y queda: √(x) = 5,5, haces pasaje de raíz como potencia, y queda: x = 30,25;
luego, reemplazas en la ecuación señalada (1), resuelves términos, y queda:
-19,5 - 5,5 = -8, resuelves el primer miembro, y queda: -25 = -8, que es una identidad Falsa, por lo que en este caso no tienes una solución del sistema;
b)
y = (-51 + 27)/8 = -3;
luego, reemplazas en la ecuación señalada (2), resuelves, y queda:
√(x) + 3 = 5, haces pasaje de término, y queda: √(x) = 2, haces pasaje de raíz como potencia, y queda: x = 4;
luego, reemplazas en la ecuación señalada (1), resuelves términos, y queda:
-6 - 2 = -8, resuelves el primer miembro, y queda: -8 = -8, que es una identidad Verdadera, por lo que en este caso si tienes una solución del sistema,
que queda expresada: x = 4, y = -3.
Espero haberte ayudado.
-
Rasyer
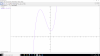
el 4/3/18Fíjate bien que en el denominador de la función tienes x + 1. Siempre que tengas funciones con denominador hay que mirar en que valores el denominador vale 0, ya que cuando el denominador vale 0 se produce una indeterminación (la función no existe en este punto, y tendremos que calcular el límite en caso de que queramos estudiarla).
En el ejemplo vemos que cuando x = -1, el denominador es ( -1 + 1 ) = 0. Por lo tanto en el punto x = -1 la función no existe.
Es por esto que el intervalo tiene que evitar el -1.
Dicho esto se ve claro que la x va de menos infinito a -1 NO INCLUIDO, y de -1 NO INCLUIDO a màs infinito. Por lo tanto todos los reales excepto el -1.
-
Me podrían dar un ejemplo fe sistemas de ecuaciones donde tenga mas ecuaciones que variables y el sistema sea compatible indeterminado , generalizada m ecuaciones y n incógnitas donde m>n
Rasyer
el 4/3/18Teniendo una matriz :
x11 x12 .... | x1n+1
x21 x22 .... | x2n+1
. . |.
. . |.
xm1 xm2 .... |xmn+1
Donde m > n, y la columna n+1 son los términos independientes y por lo tanto hay n incógnitas:
Para que sea un sistema compatible indeterminado el rango de la matriz de coeficientes tiene que ser igual al rango de la matriz ampliada, y este rango tiene que ser menor al número de incógnitas, por lo tanto ( rango(Mcoef) = rango(Mampl) ) < n.
Esto se logra creando columnas que sean combinación lineal de otras.
Un ejemplo con 3 incógnitas y 4 ecuaciones:
1 1 0 | 4
0 1 1 | 2
2 3 1 | 10
1 0 -1 | 2
La fila 3 (f3) = 2*(f1) + (f2)
La fila 4 (f4) = (f1) - (f2)
Si hiciéramos Gauss quedaría así:
1 1 0 | 4
0 1 1 | 2
0 0 0 | 0
0 0 0 | 0
Rango(Mcoef) = Rango(Mampl) = 2 (es más pequeño que el número de incógnitas (3))
Sistema compatible indeterminado.
-
Buenas podrían colaborarme con este ejercicio.
Yo plantee la ec diferencial como dT/dt = k(T-10). La resolvi y encontre las 2 constantes con las condiciones iniciales. Pero no logro llegar a la respuesta que me da el libro de log5/log2
Suponga que el ritmo al que se enfría un cuerpo caliente es proporcional a la diferencia de temperatura entre él y el ambiente que lo rodea (ley de enfriamiento de Newton). Un cuerpo se calienta 110 °C y se expone al aire libre a una temperatura de 10 °C. Al cabo de una hora su temperatura es de 60 °C. ¿Cuánto tiempo adicional debe transcurrir para que se enfríe a 30 °C?
Les agreadeceria enormemente si me echan una mano. Tengo parcial esta semana!
Antonio Silvio Palmitano
el 4/3/18Comienza por separar variables en tu ecuación diferencial, y queda:
dT/(T-10) = k*dt, integras en ambos miembros, y queda:
ln|T-10| = k*t + C (1), reemplazas los valores iniciales (t = 0, T = 110 °C), y queda:
ln|100| = C, sustituyes en la expresión señalada (1), y queda:
ln|T-10| = k*t + ln|100| (2).
Luego, reemplazas los valores correspondientes al primer instante en estudio (t = 1h, T = 60 °C) en la ecuación señalada (2), y queda:
ln|50| = k + ln|100|, haces pasaje de término, aplicas la propiedad del logaritmo de una división, y queda:
ln|1/2| = k, aplicas la propiedad del logaritmo del inverso multiplicativo en el primer miembro, y queda:
-ln|2| = k, reemplazas en la ecuación señalada (2), y queda:
ln|T-10| = -ln|2|*t + ln|100| (3).
Luego, reemplazas los valores correspondientes al segundo instante en estudio (t = a determinar, T = 30 °C) en la ecuación señalada (3), y queda:
ln|20| = -ln|2|*t + ln|100|, haces pasajes de términos, y quda:
ln|2|*t = ln|100| - ln|20|, aplicas la propiedad del logaritmo de una división en el segundo miembro, y queda:
ln|2|*t = ln|5|, haces pasaje de factor como divisor, y queda:
t = ln|5|/ln|2|.
Espero haberte ayudado.
Ángel
el 4/3/18Seguro que también te servirá:
-
Ángel
el 4/3/18Lo intento, pero no veo información clara sobre el tema y no he hecho ninguno así...por lo que perdona mis errores de antemano
g(f(x))=
g(-1) si si x< -1
g(-1) si -1 x≤ 0
g(0) si x=0
g(-1) si 0 < x≤ 1
g(1) si x>1
g(f(x))=
-12-1 si si x< -1
-1+1 si -1 x≤ 0
0+1 si x=0
-1+1 si 0 < x≤ 1
1+1 si x>1
g(f(x))=
0 si si x< -1
0 si -1 x≤ 0
1 si x=0
0 si 0 < x≤ 1
2 si x>1
|
|
v
g(f(x))=
0 si x≤ 0
1 si x=0
0 si 0 < x≤ 1
2 si x>1
-
Buenas tardes, escribo desde Argentina, estoy preparando mi examen de Análisis Matemático I y la verdad es que me han ayudado mucho los videos sobre integrales, como sugerencia, creo que estaría bueno añadir algún video con algunos ejercicios de diferenciales binomias (Método de Chebichev). Muchas gracias y saludos!
Ángel
el 4/3/18 -
Antonio Silvio Palmitano
el 4/3/18Vamos con una orientación-
Tienes en la expresión de tu enunciado (z) a dos números complejos expresados en forma exponencial (es conveniente que consultes con tus docentes, porque en esta forma los argumentos en los exponentes se deben expresar en radianes):
Luego, distribuyes el denominador en la expresión de tu enunciado, y queda:
z = 2*ei(30°) / 3*ei(45°) - 1 / 3*ei(45°) = (2/3)*ei(30°)-i(45°) - (1/3)*e-i(45°) = (2/3)*e-i(15°) - (1/3)*e-i(45°) = (2/3)*ei(-15°) - (1/3)*ei(-45°) (1).
Luego, expresas a los dos términos de la expresión señalada (1) en forma trigonométrica, y queda:
z = (2/3)*( cos(-15°) + i*sen(-15°) ) - (1/3)*( cos(-45°) + i*sen(-45°) ),
aplicas las identidades trigonométricas del coseno y del seno del opuesto de un ángulo, y queda:
z = (2/3)*( cos(15°) - i*sen(15°) ) - (1/3)*( cos(45°) - i*sen(45°) ),
distribuyes en ambos términos, y queda:
z = (2/3)*cos(15°) - i*(2/3)*sen(15°) - (1/3)*cos(45°) + i*(1/3)*sen(45°),
agrupas términos reales, agrupas términos imaginarios y extraes factor común entre ellos, y queda:
z = [ (2/3)*cos(15°) - (1/3)*cos(45°) ] + i*[ -(2/3)*sen(15°) + (1/3)*sen(45°) ];
luego, observa que tienes al número complejo cuya expresión tienes en tu enunciado, expresado ahora en forma cartesiana binómica, y tienes:
x = (2/3)*cos(15°) - (1/3)*cos(45°) (parte real de z),
y = -(2/3)*sen(15°) + (1/3)*sen(45°) (parte imaginaria de z).
Luego, tienes todo lo que necesitas para plantear el módulo y el argumento de la expresión,como seguramente has estudiado en clase.
Haz el intento de terminar la tarea y, si te resulta necesario, no dudes en volver a consultar.
Espero haberte ayudado.
-
Buenas, sigo atascado con esta derivada implícita, sé que debo usar la derivación logarítmica pero simplemente no llego al Resultado, o sea, me pierdo en el procedimiento.
y(e)2X + (X)2y =1
Respuesta: y'= -e2 -2
PD:ese es el enunciado, pues simplemente se trata de un ejercicio convencional, de práctica.