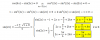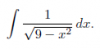-
Antonio Silvio Palmitano
el 5/2/18Debes tratar de encontrar una expresión general para las potencias de las matrices, en cada uno de los casos.
A modo de orientación, vamos con el primer ejercicio.
a)
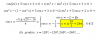
A1 = A =
3 0 31 0
3 3 = 1*31 31
A2 = A*A = (te dejo la tarea de plantear el producto) =
9 0 32 0
18 9 = 2*32 32
A3 = A2*A =
27 0 33 0
81 27 = 3*33 33
A4 = A3*A =
81 0 34 0
324 81 = 4*34 34
Luego, puedes inferir la expresión de la potencia general:
An =
3n 0
n*3n 3n, con n ∈ N, n ≥ 1.
Haz el intento con los demás ejercicios y, si te resulta necesario, no dudes en volver a consultar.
Espero haberte ayudado.
-
Hola buenas tardes, tengo un problema de ecuaciones lineales que no se por donde empezar, se hacer una ecuación lineal sin parámetros, pero cuando me dan parámetros que tengo que encontrar no se como hacerlo. Enunciado: a) Discute el parámetro en función de k. b) Resuelve la ecuación con k=2.
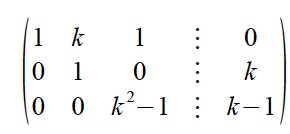
Antonio Silvio Palmitano
el 5/2/18a)
A la primera fila le restas la segunda fila multiplicada por k, y queda:
1 0 1 -k2
0 1 0 k
0 0 k2-1 k-1.
Luego, observa que si el tercer elemento de la tercera fila es distinto de cero, tienes que el sistema es compatible determinado y admite única solución.
Luego, observa que si el tercer elemento de la tercera fila es igual a cero, tienes dos casos:
1)
k = -1, reemplazas en la matriz, y queda:
1 0 1 -1
0 1 0 -1
0 0 0 -2,
y tienes que el sistema es incompatible y no admite solución;
2)
k = 1, reemplazas en la matriz, y queda:
1 0 1 -1
0 1 0 1
0 0 0 0,
y tienes que el sistema es compatible indeterminado y admite infinitas soluciones,
luego planteas el sistema de ecuaciones equivalente, y queda:
x + z = -1, aquí haces pasaje de término, y queda: z = -1 - x,
y = 1,
y tienes que el conjunto solución queda expresado:
x ∈ R,
y = 1,
z = -1 - x.
b)
Reemplazas el valor del parámetro que tienes en tu enunciado (k = 2), y la primera matriz de nuestro desarrollo (a) queda:
1 0 1 -4
0 1 0 2
0 0 3 1.
Divides a la tercera fila por 3, y queda:
1 0 1 -4
0 1 0 2
0 0 1 1/3.
A la primera fila le restas la tercera fila, y queda:
1 0 0 -13/3
0 1 0 2
0 0 1 1/3.
Luego, tienes que la solución del sistema es:
x = -13/3,
y = 2,
z = 1/3.
Espero haberte ayudado.
-
Esther
el 5/2/18Antonius Benedictus
el 5/2/18 -
Antonio Silvio Palmitano
el 5/2/18Puedes plantear la sustitución (cambio de variable):
x = 3*senw, de donde tienes:
dx = 3*cosw*dw, también tienes:
√(9 - x2) = √9 - 9*sen2w) = √( 9*(1 - sen2w) ) = √(9*cos2w) = 3*cosw,
y también tienes:
x/3 = senw, aquí compones en ambos miembros con la función inversa del seno, y queda:
arcsen(x/3) = w (1);
luego, sustituyes, y la integral de tu enunciado queda:
I = ∫ ( 1/(3*cosw) )*cosw*dw = simplificas y extraes el factor constante = (1/3)*∫dw = (1/3)*w + C;
luego, sustituyes la expresión señalada (1), y queda:
I = (1/3)*arcsen(x/3) + C.
Espero haberte ayudado.
-
Javi
el 5/2/18Para realizar esa ecuación tienes que tener una matriz cuadrada, es decir, mismo numero de filas que de columnas
Ax+B=C sería: Ax=B-C
Para despejar la x, se hace multiplicando por la matriz inversa A^-1 en ambos lados ya que A^-1*A=1, por tanto, ya se quedaría la x despejada. x=(B-C)*A^-1.
Pero para hacer la inversa necesitas que tu matriz sea cuadrada.. por eso, esa ecuación no tiene una única solución, con esto el problema estaría terminado.
Antonio Silvio Palmitano
el 5/2/18Vamos con una orientación.
Como las matriz A no es cuadrada, entonces no es invertible, y debes plantear para la matriz incógnita:
X =
x y
z w;
luego, haces pasaje de término, y queda:
A*X = B - C.
Luego, debes plantear el producto A*X (observa que te quedará una matriz de tres filas y dos columnas, cuyos elementos son expresiones con incógnitas), debes resolver la resta B - C, para luego igualar elemento a elemento, y tendrás un sistema de seis ecuaciones lineales, de primer grado y con cuatro incógnitas, que deberás resolver.
Haz el intento y, si te resulta necesario, no dudes en volver a consultar.
Espero haberte ayudado.
-
Hola Unicoos, por favor tengo una duda, cuando elaboro una grafica sofisticada, cuando debo hallar sus asintotas es obligatorio que evalue los limites por ambos lados siempre?
Ángel
el 5/2/18Si te piden hallar las asíntotas (sin especificar cuál) debes:
Estudiar las asíntotas verticales-----> Calculas los límites laterales (a ambos lados).
Estudiar las asíntotas horizontales-----> Calculas los límites en el infinito.
Estudiar las asíntotas oblicuas-----> Mira el ejemplo:
Ejemplo: