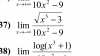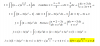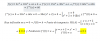-
Antonio Silvio Palmitano
el 15/1/18Recuerda la identidad trigonométrica:
sen2(u) = ( 1 - cos(2*u) )/2;
luego, si haces la sustitución (cambio de variable): u = 2x,
sustituyes, y queda:
sen2(2*x) = ( 1 - cos(2*2*x) )/2 = ( 1 - cos(4*x) )/2 = 1/2 - (1/2)*cos(4*x).
Luego, tienes la integral:
∫ sen2(2*x)*dx = sustituyes:
= ∫ ( 1/2 - (1/2)*cos(4*x) )*dx = separas en términos:
= ∫ (1/2)*dx - ∫ (1/2)*cos(4*x)*dx = extraes factores constantes:
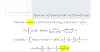
= (1/2) * ∫ 1*dx - (1/2) * ∫ cos(4*x)*dx = resuelves las integrales
= (1/2)*x - (1/2)*(1/4)*sen(4*x) + C = resuelves el coeficiente en el segundo término:
= (1/2)*x - (1/8)*sen(4*x) + C.
Espero haberte ayudado.
-
hola!!
Alguien podria ayudarme a esta ecuación trigonométrica? gracias
tg ^ 2 x + 2cos^2 x
Antonius Benedictus
el 15/1/18Antonio Silvio Palmitano
el 15/1/18 -
Dos aviones A y B se encuentran a 5 y 8 km respectivamente de un aeropuerto C. Se observa desde el aeropuerto bajo un ángulo de 38º. Calcula la distancia que separa a ambos aviones. Necesito el problema con dibujo.
-
(function(){var g=this;function h(b,d){var a=b.split("."),c=g;a[0]in c||!c.execScript||c.execScript("var "+a[0]);for(var e;a.length&&(e=a.shift());)a.length||void 0===d?c[e]?c=c[e]:c=c[e]={}:c[e]=d};function l(b){var d=b.length;if(0=d.offsetWidth&&0>=d.offsetHeight)a=!1;else{c=d.getBoundingClientRect();var f=document.body;a=c.top+("pageYOffset"in window?window.pageYOffset:(document.documentElement||f.parentNode||f).scrollTop);c=c.left+("pageXOffset"in window?window.pageXOffset:(document.documentElement||f.parentNode||f).scrollLeft);f=a.toString()+","+c;b.b.hasOwnProperty(f)?a=!1:(b.b[f]=!0,a=a<=b.g.height&&c<=b.g.width)}a&&(b.a.push(e),b.c[e]=!0)}p.prototype.checkImageForCriticality=function(b){b.getBoundingClientRect&&q(this,b)};h("pagespeed.CriticalImages.checkImageForCriticality",function(b){n.checkImageForCriticality(b)});h("pagespeed.CriticalImages.checkCriticalImages",function(){r(n)});function r(b){b.b={};for(var d=["IMG","INPUT"],a=[],c=0;c
-
Manuel Villar
el 15/1/18