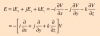-
Francisco
el 20/11/18Me podrían resolver el ejercicio 29?
Antonio Silvio Palmitano
el 20/11/18Establece un sistema de referencia, con eje de posiciones Or con origen en el centro de la Tierra, con dirección y sentido positivo hacia el centro de la Luna.
Luego, tienes los datos:
rL = 3,84*105 Km = 3,84*108 m (posición del centro de la Luna),
ML = 0,012*MT (1) (masa de la Luna en función de la masa de la Tierra).
rP = a determinar (posición del punto en estudio).
Luego, planteas las expresiones de los campos gravitatorios que la Tierra y la Luna ejercen sobre el punto en estudio (observa que los signos de las expresiones indican los sentidos de los campos), y queda:
ET = -G*MT / rP2 (2),
EL = G*ML / (rL-rP)2 (3).
Luego, planteas la condición que tienes en tu enunciado (el campo resultante es nulo en el punto en estudio), y queda:
ET + EL = 0, restas EL en ambos miembros, y queda:
ET = -EL, sustituyes las expresiones señaladas (2) (3), y queda:
-G*MT / rP2 = -G*ML / (rL-rP)2, sustituyes la expresión señalada (1) en el segundo miembro, y queda:
-G*MT / rP2 = -G*0,012*MT / (rL-rP)2, divides en ambos miembros por -G*MT, y queda:
1/ rP2 = 0,012 / (rL-rP)2, multiplicas en ambos miembros por rP2*(rL-rP)2, y queda:
(rL-rP)2 = 0,012*rP2, desarrollas el primer miembro, y queda:
rL2 - 2*rL*rP + rP2 = 0,012*rP2, restas 0,012*rP2 en ambos miembros, y queda:
rL2 - 2*rL*rP + 0,988*rP2 = 0, ordenas términos, y queda:
0,988*rP2 - 2*rL*rP + rL2 = 0, reemplazas el valor de la posición de la Luna, resuelves coeficientes, y queda:
0,988*rP2 - 7,68*108*rP + 1,47*1017 = 0,
que es una ecuación polinómica cuadrática, cuyas soluciones son:
rP = ( 7,68*108 ± 0,94*108 ) / 1,976,
por lo que tienes dos opciones:
a)
rP = 4,36*108 m,
que no tiene sentido para este problema, porque no corresponder a una posición intermedia entre la Tierra y la Luna;
b)
rP = 3,41*108 m,
que sí tiene sentido para este problema, porque sí corresponder a una posición intermedia entre la Tierra y la Luna.
Espero haberte ayudado.
-
Jaime
el 20/11/18Buenas tardes:
Tengo que transformar: Utilizando factores de conversión, no entiendo muy bien como se hace. ¿Qué pasos hay que seguir? Me podéis ayudar con una explicación. Gracias.
38 cm2 a Gm2
437 m3 a μm3
Antonio Silvio Palmitano
el 20/11/18Vamos paso a paso, a ver si te resultan útiles estos desarrollos.
Recuerda que los factores de conversión son expresiones fraccionarias iguales a 1, pero con el numerador y el denominador expresados con unidades de medida distintas.
1)
Observa unidad inicial es cm2, por lo que debes ubicarla en el denominador del factor de conversión, para luego simplificarla,
luego tienes;
1 Gm2 = (1*1012 m)2 = (1*1012*102 cm)2 = (1*1014 cm)2 = 1*1028 cm2,
luego, con el primero y el último miembro de la cadena de igualdades, tienes la identidad:
1 Gm2 = 1*1028 cm2,
divides por 1028 cm2 en ambos miembros, y queda:
1 Gm2 / 1028 cm2 = 1,
asocias el factor y el divisor numérico, asocias el factor y el divisor literal, y queda:
(1/1028) Gm2/cm2 = 1,
aplicas la propiedad de las potencias con exponentes negativos en el factor fraccionario numérico, y queda:
10-28 Gm2/cm2 = 1,
y tienes que el factor de conversión es la expresión remarcada en el primer miembro.
Luego, vamos a tu ejercicio:
38 cm2 = 38 cm2 * (10-28 Gm2/cm2) = simplificas = 38*10-28 Gm2= 3,8*10-27 Gm2.
2)
Observa unidad inicial es m3, por lo que debes ubicarla en el denominador del factor de conversión, para luego simplificarla,
luego tienes;
1 m3 = (1*106 μm)3 = 1*1018 μm3 = 1018 μm3,
luego, con el primero y el último miembro de la cadena de igualdades, tienes la identidad:
1 m3 = 1018 μm3,
divides por m3 en ambos miembros, y queda:
1 = 1018 μm3 / m3,
y tienes que el factor de conversión es la expresión remarcada en el segundo miembro.
Luego, vamos a tu ejercicio:
437 m3 = 437 m3 * (1018 μm3 / m3) = simplificas = 437*1018 μm3 = 4,37*1020 μm3.
Espero haberte ayudado.
-
carmela
el 20/11/18Buenas tardes. He intentado hacer el problema siguiendo el enlace que me dio Raul, pero no lo consigo. Si me pudierais echar una mano porfa.
Jerónimo
el 20/11/18Separamos el problema en dos partes, antes y después de despegar las patas del suelo.
ANTES
La fórmula de la cinemática que relaciona velocidad, aceleración y espacio es V²-Vo²=2ae, en este caso Vo=0, nos queda V=√2ae,siendo a la aceleración que nos piden y e la altura de la extensión de patas .
DESPUES
La única aceleración que hay es la gravedad, se puede aplicar conservación de energía o cinemática, más sencillo por energías 1/2mV²=mgh, siendo V , la velocidad con la que comienza el ascenso V=√2gh
Igualando √2ae =√2gh a=gh/e=02g/0,02=10g
-
Cesar
el 20/11/18Hola, algun genio que me ayude con este ejercicio por favor, gracias!
-
Juan C
el 20/11/18saludo. necesito ayuda con este ejercicio. Muchas gracias.
Jerónimo
el 20/11/18Aplicas Bernoulli , 1/2ρv1^2 +ρgh1+P1=1/2ρv2^2 +ρgh2+P2
Llamando 1 a la parte superior donde empieza a bajar el agua y 2 a la abertura, simplificando P1=P2 (p atmosférica) y v2 mucho mayor que vi y tomando como cero de altura la parte de abajo , queda
ρgh1=1/2ρv2^2 v2=√2gh=√2x9,8x4= 8,85m/s
Si la sección es de 1cm2, caudal Q=A x v=1x10^-4 m2 x 8,85m/s = 0,88 x10^-3 m3/s
-
Joel Aday Dorta Hernández
el 19/11/18
Raúl RC
el 19/11/18a) Correcta, con sustituir las componente de los puntos obtienes el mismo resultado:
b) Incorrecta, el gradiente se define como las derivadas parciales respecto a cada componente, con lo cual la derivada en "x" y en "z" serían cero.
Este vídeo sobre gradiente te ayudará
https://www.youtube.com/watch?v=hQjPW5hsU2o
c) Correcta. El campo electrico se obtendria derivando cada componente respecto a "x" "y" y "z" con lo cual te quedaria:
Si haces esto te queda E=-2j V/m
d) Falsa, faltaria el signo negativo como puedes ver en la expresión anterior.
e) f) te las dejo a ti
Un saludo
-
FA7
el 19/11/18
Hola necesito ayuda con este ejercicio. Gracias
Por el interior de un valle sopla una corriente de vientos, cuya velocidad se ha ajustado en un instante determinado al campo vectorial siguiente: 𝑣⃗=(2𝑦𝑒−3𝑥) 𝑖⃗+(4𝑦2𝑧) 𝑗⃗+(𝑦𝑒3𝑧) 𝑘⃗⃗
El origen de coordenadas (x, y, z) se ha colocado en un punto a la entrada del valle y las coordenadas se miden en km desde dicho punto. Por otra parte, las componentes de la velo-cidad (vx, vy, vz) se obtienen en dicha ecuación en cm/s. En el instante en que se ha medido el campo de vientos, todo el valle se encontraba a la misma presión y temperatura.
Calcular:
a) El valor de la divergencia de la velocidad del viento en un punto que está a 3 km del origen en dirección +x, y se sitúa a 500 m de altura (dirección +z). ¿Hay probabilida-des de que aumente la presión en dicho punto con el paso del tiempo?
b) La ecuación que representa el campo de divergencias de la velocidad del viento a ras del suelo.
c) El valor del rotacional de la velocidad del viento en un punto del valle que se posi-ciona del siguiente modo. Situados en el origen de coordenadas con un visor apun-tando a la dirección +x, se rota el visor en el sentido anti-horario 30º10’20’. Después se alza el visor 20º30’10’’ y, finalmente, se enfoca el visor a una distancia de 700 m. ¿Hay probabilidades de que se desarrolle un remolino de viento en dicho punto?
Considérese que el aire se comporta como un gas ideal.
-
Juan C
el 19/11/18 -
Sofia
el 19/11/18buenas tardes! tengo dudas sobre como resolver este problema
considere una estufa electrica con dos velas, cuyas especificaciones correspondientes a cada vela, son "220V-600W"
a) calcule la resistencia electrica de cada vela, y la corriente que circula por ella en funcionamiento normal
b) suponiendo que se hace trabajar la estufa con las dos velas encendidas, indique si ellas quedan conectadas en serie o en paralelo, y explique la razon.
Raúl RC
el 19/11/18a) La potencia se define como P=V·I y a su vez aplicando la ley de Ohm V=I·R =>I=V/R, sustituyendo:
P=V2/R =>R=V2/P=80,66 Ω
La intensidad será:
I=200/80,66=2,48 A
b) Se hacen trabajar en paralelo porque de esta forma al intensidad de corriente al repartirse por ellas genera el mismo voltaje en cada una, con lo cual a las dos les llega una tensión de 220V
La asociación en serie solamente se explica desde un punto de vista didáctico, pues en la vida real no es práctico ya que la tensión que pasa por cada resistencia no es la misma, con lo cual no pueden rendir con todo su esplendor
