Hay algo que se suponga fijo o constante?

En términos mas generales θ  = ½ α donde α es el angulo entra la cuerda horizontal y la vertical.

Linea del estado? A que distancia se encontraría la linea del estado?

Debes conocer esa distancia para resolver el sistema de ecuaciones.

O bien, plantearla como un parámetro. En cuyo caso la respuesta sería una aceleración que depende de dicho parámetro.

Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

Unicoos llega exclusivamente hasta secundaria y bachillerato

Revisa el enunciado. El sistema no puede estar en equilibrio salvo tensiones dirigidas en sentido opuesto a las supuestas tensiones mismas (o barras en lugar de cuerdas). Mas allá de eso, técnicamente los resultados a los que has llegado son correctos. Los signos negativos indican sentidos opuestos a los asumidos.

Supongo que la fuerza de rozamiento no actúa durante la compresión del resorte.

El trabajo W realizado por una fuerza constante durante un recorrido Δs es: W = F Δs cos(λ) donde λ es el angulo entre F y Δs.

Si F y Δs están alineados (λ = 0, o 180°) Entonces: W = F Δs

Para un resorte lineal (que obedece a la ley de hooke), la energía potencial elástica acumulada E_pe es E_pe = ½ kx², donde k es la constante elástica, y x es la deformación. Notese que el dato de k esta en kilo Newtons.

Por conservación de la energía, Conociendo la energía cinética con la que el bloque llega al resorte, podemos igualar en E_pe y despejar x.

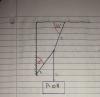
Altura inicial y angulo del plano inclinado.

El angulo α que forma el plano respecto a la horizontal se deduce del pequeño triangulo de base 4 y altura 3: tg(α) = 3/4  => α = arctan(3/4) = 36.9°

Luego, la altura inicial h = 7.6 sin(36.9) = 4.56 m

Parte 1. Plano inclinado.

Energía inicial. El bloque parte del reposo, de modo que su energía cinética inicial es 0. Toda la energía inicial es entonces su energía potencial gravitatoria E_pg.

E_pg = mgh = 30.6*9.8*4.56 = 1367 J. Si no existieran perdidas de energía por rozamiento, al finalizar el plano inclinado, toda su energía potencial gravitatoria se habría convertido en energía cinética. Pero como hay perdidas, la energía cinética E_c en ese momento sera entonces: E_c = E_pg - E_r donde E_r es el trabajo realizado por la fuerza de rozamiento F_r.

Fuerza de rozamiento y trabajo de la fuerza de rozamiento.

F_r = µN.  N = P cos(α) = mg cos(α) = 240N  => F_r = 0.2*240 = 48 N. Y como µ y N son constantes durante todo el recorrido de plano inclinado, F_r también lo es.

El trabajo W_r realizado por tanto W_r = F_r Δs. El recorrido Δs es 7.60 m por lo tanto W_r = 48*7.6 = 365 J. Energía perdida por rozamiento, que habíamos llamado E_r 

Por tanto, E_c al finalizar el plano inclinado es E_c = 1367 - 365 = 1002 J

Parte 2. Plano horizontal.

La altura permanece constante. No hay variaciones de la E_c por motivos de la fuerza gravitatoria. Solo hay perdidas producto del rozamiento que en este caso es:

F_r = μN = μ mg = 60N, y el trabajo realizado en el recorrido de 2.75 (2.75? veo bien?) es W_r = 60*2.75 = 165j. Luego E_c al final del plano horizontal es 1002 - 165 = 837J

En resumen. El bloque parte del reposo con una E_pg de 1367J. Mientras recorre el plano inclinado pierde por rozamiento una energía de 365j. De modo que comienza el movimiento en el plano horizontal con una E_c de 1002J. Y durante el movimiento horizontal disipa una energía de 165j. De modo que llega al resorte con una E_c de 837J.

Deformación del resorte.

La deformación máxima del resorte sucederá cuando toda la E_c con la que el bloque alcanza al resorte se transforme en E_pe 

E_pe = ½ kx²  => x² = 2E_pe/k  =>  x = √2E_pe/k). Y si suponemos que no hay perdidas por rozamiento durante la compresión podemos igualar E_pe a la E_c con la que el bloque alcanza el resorte.

Luego x = √2*837/18000) = 0.305 m

Por si lo piden con la fuerza de rozamiento actuando durante la compresión y lo manejan con algo mas de matemática.

El trabajo W realizado por una fuerza F  es: W = ∫ Fdx entre a y b, si F y dx son colineales.

La fuerza ejercida por el resorte F_k es: F_k = kx  y F_r es como ya se ha dicho F_r = μN.

Estableciendo un sistema de coordenadas con origen al finalizar el plano horizontal, el extremo inferior de integración a  es a = 0 y el extremo superior b es un b tal que W = 837J.

Como la fuerza de rozamiento y la fuerza del resorte tienen igual sentido la fuerza neta F_n es: F_n = F_k + F_r = kx + μN.

Luego: W = ∫ F_n dx = ∫ F_k + F_r dx= ∫ kx + μN dx =  ∫ kx dx + ∫ μN dx =  k ∫ x dx + μN ∫ dx = ½kx² + μNx 

Entonces:  (½kb² + μNb) - (½ka² + μNa) =  ½kb² + μNb = 837  => 9000b² + 60b - 837 =0  => b = 0.301644 = 0.302m  

Para que la bola se encuentre en equilibrio, debe de haber una fuerza horizontal hacia la derecha de 100 N. Siendo x horizontal e y vertical:

Si dicha fuerza equilibrarte es únicamente producto de la tensión T, entonces, dicha fuerza es la componente horizontal de T, T_x

Por trigonométrica. T_x = T sen(37°) => T = T_x/sen(37°)    y como T_x = 100 ( por condición de equilibrio)   => T = 100/sen(37°) = 166N

Las respuestas están equivocadas. Posiblemente aplicaron T_x = T cos(α), quizás por costumbre ya que en general el dato es el angulo respecto a la horizontal y daría como resultado 125,  pero es incorrecto.

Según ese angulo α de 37°. T_x = T sen(α)    y    T_y = T cos(α).

Sr. Fernando Alfaro, concuerdo con usted sobre la respuesta, segun el libro la respuesta es 75N. El problema es un ejercicio de admision universitaria.

Perdón. Conociendo la respuesta creo que ya entendí lo que verdaderamente está pidiendo el enunciado. 100N no es el modulo del vector representado, es el peso de la bola. Y lo mas confuso del enunciado, lo que se pide no es la tensión T en la cuerda sino la componente horizontal T_x de la tensión T.

La tensión T se calcula entonces igualando su componente vertical al peso de la bola: Ty = T cos(37°) = 100  => T = 125 N

Y su componente horizontal es entonces Tx = T sen(α) = 125*sen(37) = 75 N.

Pero es aplicando ingeniería inversa al confuso enunciado.

De dimensiones de?

La solución podría ser una posición que se encuentra a la izquierda de q₂. Luego calculas las distancias entre cargas.

También podría ser a la derecha de q₃. Pero por los valores prometo que si hay solución en donde las fuerzas se anulan, es a la izquierda de q₂