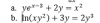-
Antonio Silvio Palmitano
el 22/11/19Vamos con una orientación.
a)
Derivas implícitamente con respecto a x (recuerda que consideramos que y es una función de x), observa que en el primer término tienes una multiplicación de funciones, y queda:
y'*ex-3 + y*ex-3 + 2*y' = 2*x, restas en ambos miembros, y queda:
y'*ex-3 + 2*y' = 2*x - y*ex-3, extraes factor común (y') en el primer miembro, y queda:
y'*(ex-3 + 2) = 2*x - y*ex-3, divides por (ex-3 + 2) en ambos miembros, y queda:
y' = (2*x - y*ex-3)/(ex-3 + 2),
que es la expresión de la función derivada, y observa que está definida para todo valor de la variable independiente (x), con su correspondiente valor de la ordenada (y), ya que la expresión del denominador toma valores estrictamente mayores que dos y, por lo tanto, también distintos de cero.
b)
Comienza por aplicar la propiedad del logaritmo de una multiplicación en el primer término, y la ecuación de tu enunciado queda:
ln(x) + ln(y2) + 3*y = 2*y3, aplicas la propiedad del logaritmo de una potencia en el segundo término, y queda:
ln(x) + 2*ln(y) + 3*y = 2*y3;
luego, derivas implícitamente con respecto a x (recuerda que consideramos que y es una función de x), y queda:
1/x + 2*(1/y)*y' + 3*y' = 6*y2*y', multiplicas por x y también por y en todos los términos, y queda:
y + 2*x*y' + 3*x*y*y' = 6*x*y3*y', restas 6*x*y3*y', y también restas y, en ambos miembros, y queda:
2*x*y' + 3*x*y*y' - 6*x*y3*y' = -y, extraes factores comunes en el primer miembro, y queda:
y'*x*(2 + 3*y - 6*y3) = -y, divides en ambos miembros por [x*(2 + 3*y - 6*y3)], y queda:
y' = -y/[x*(2 + 3*y - 6*y3)],
que es la expresión de la función derivada, y observa que está definida para todo valor de la variable independiente (x), con su correspondiente valor de la ordenada (y), mientras se cumpla con la condición:
x*(2 + 3*y - 6*y3) ≠ 0.
Espero haberte ayudado.
-
 Hola de nuevo, he cambiado las identidades notables del sistema de ecuaciones trigonométricas y me ha salido algo aún más raro. Me podría alguien decir como se hace?
Hola de nuevo, he cambiado las identidades notables del sistema de ecuaciones trigonométricas y me ha salido algo aún más raro. Me podría alguien decir como se hace?
-
Buenas noches, he intentado hacer este sistema de ecuaciones trigonométricas pero tengo duda ya que al obtener alfa, lo he hecho de dos formas distintas y me salen diferentes, no se si es por haberlo elevado todo al cuadrado. Tampoco se si lo que he hecho anteriormente está bien.

Jose Ramos
el 21/11/19 -
¿Alguien me puede decir si están bien?El segundo lo he preguntado antes pero me han dicho que el resultado tenia que ser -4/(pi)^2
Jose Ramos
el 21/11/19El primero lo tienes mal. Te falto tomar el Ln de la base cuando pasas el exponente multiplicando.
El segundo ahora lo tienes bien . El resultado que te di antes de -4/(pi)^2 era porque tenías invertido el cociente y al final te daba (pi)^2 / 4, pero había algún error en el cálculo final. AHORA ESTÁ BIEN
-
Alguien me puede ayudar a resolver los siguientes problemas:
1. Con un telescopio de observación se mide que el picacho de San José se encuentra en dirección N 22°23´ E y el picacho de San Jazmín N 67° 37´ O. Una placa de bronce nos indica que la distancia rectilínea al picacho de San José es de 45,82 km y al picacho de San Jazmín 38,36 km. Se desea saber la distancia entre los dos picachos.
2. Un piloto vuela con velocidad respecto al aire de 220 km por hora y en dirección 148°20´. El viento sopla del este a 16km por hora. Encuéntrese la velocidad del avión respecto a la tierra y la dirección de vuelo.
3. Dos calles se cruzan en un ángulo de 123° 40´. Un terreno en la esquina tiene 94,6m de frente en unas de las calles y 93,8 en la otra. ¿Cuál será la longitud del muro en la parte posterior del terreno?
4. Un diseñador calcula que un remache va a soportar unas cargas de 876 kilos y 988 kilos con un ángulo entre ellas de 59° 40´. ¿Cuál será la fuerza resultante?
Breaking Vlad
el 24/11/19se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)