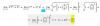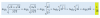-
Para elevar volantines se utiliza un carrete circular que tiene 2,7 metros de hilo, el cual equivale a cuatro vueltas y media. Si pi= 3, ¿cuál es el diámetro del carrete?
La respuesta es 20,pero como llego a eso?,gracias de antemano.
Jose Ramos
el 16/11/191 vuelta de carrete equivale al perímetro del mismo que es 2πr = πD (siendo D el diámetro del carrete). Como los 2,7 m. de hilo equivalen a 4,5 vueltas, tenemos:
2,7 = 4,5 πD; de donde: D = 0,6/π. Si tomamos π = 3,1416 resulta que D = 0,1907 m. que es igual a 19,07 cm.
-
Antonio Silvio Palmitano
el 16/11/19Observa que la longitud de la base del rectángulo es: b = p + 3p = 4p, y que llamamos h a su altura.
Luego, planteas las expresiones de las áreas del rectángulo, de los triángulos y del trapecio que tienes indicados en tu enunciado, y queda:
AR = 4*p*h,
ADEF = 3*p*h/2,
AAED = p*h/2,
AEBCF = (3p + p)*h/2 = 4p*h/2 = 2*p*h.
Luego, pasamos a considerar cada una de las opciones que tienes expresadas en tu enunciado.
I)
Planteas la razón entre las áreas de los dos triángulos que tienes indicados, y queda:
ADEF/AAED = (3*p*h/2)/(p*h/2) = simplificas = 3, por lo que tienes que la proposición planteada es Verdadera.
II)
Planteas la razón del área del triángulo que tienes indicado entre el área del rectángulo, y queda:
ADEF/AR = (3*p*h/2)/(4*p*h) = simplificas = (3/2)/4 = resuelves = 3/8, por lo que tienes que la proposición planteada es Verdadera.
III)
Planteas la razón del área del triángulo que tienes indicado entre el área del trapecio, y queda:
ADEF/AEBCF = (3*p*h/2)/(2*p*h) = simplificas = (3/2)/2 = resuelves = 3/4, por lo que tienes que esta proposición es Verdadera.
Luego, puedes concluir que la opción señalada (E) en tu solucionario es la respuesta correcta.
Espero haberte ayudado.
-
Ayuda Por favor El 2 de mayo del año 1 se depositan $15 000 y a partir del 2 de noviembre del año 3
y hasta el 2 de mayo del año 5 se depositan cada 6 meses $8 000 en una cuenta que
abona 8% semestral. ¿Cuánto se habrá acumulado al 2 de noviembre del año 10?Es relacionado a la anualidad diferida
Antonio Silvio Palmitano
el 16/11/19Observa que tienes tres fechas importantes:
2 de mayo del año 1: se depositan 15000 pesos,
2 de noviembre del año 3: comienzan los depósitos adicionales de 8000 pesos,
2 de mayo del año 3: se efectúa el último depósito adicional,
2 de noviembre del año 3: no se hacen más depósitos adicionales,
2 de noviembre del año 10: se obtiene el monto final.
Observa que tienes:
un periodo "largo" desde el 2 de mayo del año 1 hasta el 2 de noviembre del año 3,
un periodo semestral desde el 2 de noviembre del año 3 hasta el 2 de mayo del año 4,
un periodo semestral desde el 2 de mayo del año 4 hasta el 2 de noviembre del año 4,
un periodo semestral desde el 2 de noviembre del año 4 hasta el 2 de mayo del año 5,
un periodo semestral desde el 2 de mayo del año 5 hasta el 2 de noviembre del año 5,
un periodo "largo" desde el 2 de noviembre del año 5 hasta el 2 de noviembre del año 10,
y observa que el monto final de cada periodo constituye el capital inicial del periodo siguiente.
Luego, todo consiste en plantear los capitales iniciales y montos finales para cada periodo.
Observa que desde el 2 de mayo del año 1 hasta el 2 de noviembre del año 3, tienes cinco semestres, por lo que el monto final es:
M1 = 15000*(1 + 0,08)5 ≅ 22039,92 pesos.
Luego, observa que el capital total depositado el 2 de noviembre del año 3 es: C2 ≅ 22039,92 + 8000 ≅ 30039,92 pesos,
y que el monto a fin de semestre es: M2 = C2*(1 + 0,08) ≅ 30039,92*1,08 ≅ 32443,11 pesos.
Luego, observa que el capital total depositado el 2 de mayo del año 4 es: C3 ≅ 32443,11 + 8000 ≅ 40443,11 pesos,
y que el moto a fin de semestre es: M3 = C3*(1 + 0,08) ≅ 40443,11*1,08 ≅ 43678,56 pesos.
Luego, observa que el capital total depositado el 2 de noviembre del año 4 es: C4 ≅ 43678,56 + 8000 ≅ 51678,56 pesos,
y que el monto a fin de semestre es: M4 = C4*(1 + 0,08) ≅ 51678,56*1,08 ≅ 55812,84 pesos.
Luego, observa que el capital total depositado el 2 de mayo del año 5 es: C5 ≅ 55812,84 + 8000 ≅ 63812,84 pesos,
y que el moto a fin de semestre es: M5 = C5*(1 + 0,08) ≅ 63812,84*1,08 ≅ 68917,87 pesos.
Observa que desde el 2 de noviembre del año 5 hasta el 2 de noviembre del año 10, tienes diez semestres, observa que el capital total depositad en esta fecha es: 68917,87 por lo que el monto final es:
Mf ≅ 69817,87*(1 + 0,08)10 ≅ 148788,51 pesos.
Espero haberte ayudado.
Usuario eliminado
el 16/11/19Antonio Silvio Palmitano como puedo contactarme contigo para que me expliques el ejercicio?, porque lo resuelves calculando el monto semestre por semestre?. osea apenas estoy empezando en este tema y no puedo entender.
Yo pensaba utilizar la formula
M=R (1+i)n - 1 / i para los 3 semestres de noviembre del año 3 a mayo del año 5
y luego sumar con el:
M= R (1+i)n - 1 / i de los 11 semestres de mayo año 5 hasta noviembre año 10
ayudame porfavor
-
Hola a todos, como demuestro que la inversa de una matriz triangular superior invertible es triangular superior. Pero sin determinantes ni adjuntas. Muchas gracias
César
el 16/11/19 -
Como es posible que la letra "Z" tenga centro de simetria,alguien me lo puede explicar porfa?Muchas gracias de antemano¡