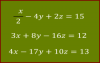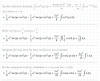-
Facu Imfeld
el 15/3/17Buenas, tengo un problema bastante tonto pero es que no le puedo encontrar el porque..
Tengo la siguiente integral definida
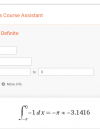
∫(-1).dx evaluada entre -π y 0
Siendo -π su extremo inferior y 0 su extremo superior
Probé con todos los softwares posibles y el resultado es π, pero a mi me da -π y no le encuentro el porque
Aclaro que según los conocimientos que tengo de teoría de integrales, en ese ejercicio puedo sacar el -1 afuera por ser una constante, de modo que si integro dx me quedaría como resultado x, evaluado entre -π y 0
Si reemplazo los extremos en el resultado de la integral me queda:
(0)-(-π) = π --> pero si a esto le multiplico el -1 que saque afuera me queda -π
¿Alguien me puede explicar en dónde está la falla? Desde ya muchas gracias por su atención
Antonio Silvio Palmitano
el 15/3/17Debes tener cuidado con los signos cuando evalúas.
Tienes la integral para evaluar entre -π y 0:
I = ∫(-1)dx = extraes el factor constante = -1*∫1dx =
integras (indicamos con corchetes que debemos evaluar con la Regla de Barrow):
= - 1*[ x ] = evaluamos = - 1*[ 0 - (-π) ] = - 1*π = - π.
Espero haberte ayudado.
-
Fernando
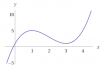
el 15/3/17hola gente tengo un problema para hallar las raíces de este polinomio x^3-6x^2+9x+1 , probé con ruffini y no me da.. lo estuve trabajando algebraicamente y no llego a un resultado en concreto, pareciera que tuviese raiz doble en 3 pero no estoy seguro
saludos
Antonio Silvio Palmitano
el 15/3/17
Antonius Benedictus
el 15/3/17
Fernando
el 16/3/17voy a ver eso de la formula , estoy en las primeras clases de Análisis matemático 2 , y de polinomios siempre trabajaba con ruffini u otros métodos de factorizacion pero nunca me paso esto de que no llegue a resultados concretos, que otros métodos sugieren ademas de la formula de cardano??
desde ya muchísimas gracias por la ayuda
-
Judit
el 15/3/17Dado f(x)=xe^(-x^2), busca un punto de f(x) en el que la pendiente de la recta tangente sea máxima. En mis apuntes tengo puesto esto, pero no sé por qué va hasta la 3a derivada si la pendiente se obtiene con la 1a
Antonio Silvio Palmitano
el 15/3/17Observa que te pide información sobre la función "pendiente de la recta tangente", por lo tanto tenemos que la función a optimizar (M) tiene su expresión igual a la derivada primera de la función f, que es la que expresa la pendiente de las rectas tangentes trazadas en cualquier punto de la gráfica de f. Por lo tanto, planteamos:
M(x) = f ' (x), sustituimos y queda:
M(x) = e-x^2 - 2x2e-x^2
luego, observa que las expresiones de las derivadas primera y segunda de la función M coinciden con las expresiones de las derivadas segunda y tercera de la función f, respectivamente.
Espero haberte ayudado.
-
Rafael J Gonzalez Rodriguez
el 15/3/17Muy buenas: solicito la ayuda con el siguiente ejercicio de ecuaciones de 3 x 3, llevo mas de 30 página en apuntes tratándolo de resolver los diferentes métodos que hay (igualación, reducción, sarrus), gracias por su ayuda.
Método de Sarrus;
Determinante del sistema:3/2
-4
2
3
8
-16
4
-17
10
3/2
-4
-2
3
8
-16
20+102+256)-(64+480-120)
=(478)-(424)
=54
Determinante de x:15
-4
2
12
8
-16
13
-17
10
15
-4
-2
12
8
-16
=(1200+408+832)-(208+4080-480)
=(2440)-(3808)
=-1368
Determinante de y:
3/2
15
2
3
12
-16
4
13
10
3/2
15
-2
3
12
-16
=(180-78-960)-(96-312+450)
=(-858)-(234)
=-1092
Determinante de z:
3/2
-4
15
3
8
12
4
-17
13
3/2
-4
15
3
8
12
=(156-765-192)-(480-306-156)
=(-801)-(18)
=-819
Estos son algunos de los resultado obtenidos:
Gracias,
Rafael González
Colombia
-
Rosa Fernandez
el 15/3/17
Usar un operador de proyección T: R2 --> R3 para proyectar un triangulo ubicado en el plano XY de R2, al espacio R3 en su cuadrante 1º, que no sea coplanar a ninguno de los planos XY, XZ, YZ de R2.
David
el 17/4/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
:)
el 15/3/17hola me ayudan con este sistema parametrico
muchas gracias
ax+2y-3z=5 x-2y+3z=7 -2x+3y-2z=4
-
Facu Imfeld
el 15/3/17 -
José Emanuel
el 15/3/17 -
magui
el 15/3/17
Buenas noches, me podrian orientar con Está demostración de triangulos, no se ni como plantear mi tesis, no se me ocurre Cómo. Agradeceria la ayuda.
Antonius Benedictus
el 15/3/17Si los ángulos de un triángulo son A, B, C, los ángulos exteriores serán: 180-A, 180-B y 180-C
Los ángulos exteriores de un triángulo suman: (180-A)+(180-B)+(180-C)=180+180+180-(A+B+C)=360
Si hubiera solo uno obtuso y los otros dos no, tendríamos un ´ngulo entre 90 y 180 más dos entre 0 y 90, su suma NUNCA valdría 360º.
-
María Juliana Aparicio A.
el 15/3/17Hola, tengo este problema que no sé cómo resolver y agradecería mucho si me pudieran explicar cómo hacerlo. El problema es el siguiente:
Para medir los lados de una zona cuadrada se utilizan figuras de 2, 3, 4 y 5 centímetros, de manera que cada lado se mide con una y solo una de las figuras. Si el número de figuras utilizadas para medir cada lado es exacto, entonces el área mínima que puede tener el cuadrado es:
A. 2000
B. 2800
C. 3600
D. 6000
Ángel
el 15/3/17Tendrás que hacer el mínimo común múltiplo de (2,3,4 y 5)
2: 21
3: 31
4: 22
5: 51
m.c.m=60 cm tendrá cada lado del cuadrado como mínimo (un lado 30 figuras de 2cm, otro 20 de 3 cm, el tercer lado 15 figuras de 4 cm y el último 12 de 5cm)
Entonces el área mínima será (60*60) cm2= 3600 cm2
