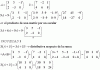-
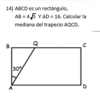
Me ayudan con esta pregunta de geometria plz, segun yo falta un dato que te digan para poder resolverlo ya que uno no se puede guiar por la imagen al 100%
-
La probabilidad de que Juan tome un bus al trabajo en cualquier mañana es 0,4. ¿Cuál es la probabilidad que en una semana de trabajo de 5 días Juan tome un bus solamente dos veces?
La respuesta es 0,3456 ,como puedo desarrollarlo,muchisimas gracias¡¡¡¡¡
-
Se lanza una moneda y dos dados comunes, uno a continuación del otro. ¿Cuál es la probabilidad de que en la moneda salga cara y de que el número del primer dado sea menor que el número del segundo?
La respuesta es 15/72 ,pero como podria desarrollarlo muchas gracias¡¡
-
Si se lanzan 5.000 veces dos dados comunes, entonces según la Ley de los Grandes Números, ¿en qué porcentaje, aproximadamente, de esas repeticiones, ocurrirá que la suma de los números obtenidos será mayor o igual a 6?
La respuesta es 72%,pero como podria calcular eso? graciass¡
-
Buenas noches,
Sean a,b,c, d ∈ ℤ positivos tales que cumplen que cumplen a×b=c×d, demuestra que a+b+c+d nunca puede ser un número primo.
Comparto desarrollo propio hasta donde ya no puedo continuar:
Despejando de ab=cd => a=cd/b ; b=cd/a ; c=ab/d ; d=ab/c.
Sustituyo los valores en la suma.
cd/b + cd/a + ab/d + ab/c
cd×(a+b/ab) + ab(c+d/dc)
Si ab y dc son iguales se pueden sustituir.Sé que este punto está el truco que no veo.
cd×(a+b/cd) + ab(c+d/ab) => a+b+c+d
Gracias por leer y espero una respuesta.
-
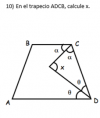
Buenas tardes, en el examen me han preguntado cual Es la relación entre límites y curvas de nivel y no supe que responder, cuál sería la relación entre ambas? Gracias
-
(1/a)+(1/b)=2
como lo resuelvo y como argumento la respuesta


Antonio Silvio Palmitano
el 2/10/19Si tienes un sistema de ecuaciones, en la cuál una de ellas es la ecuación de tu enunciado, por favor envía el enunciado completo.
De todas maneras, vamos con una orientación para esta ecuación.
Observa que las incógnitas a y b no pueden tomar el valor cero.
Luego, multiplicas por a y por b en todos los términos de la ecuación, simplificas en los términos del primer miembro, y queda:
b + a = 2ab;
luego, si eliges despejar b, puedes restar 2ab y restar a en ambos miembros, y queda:
b - 2ab = -a, extraes factor común en el primer miembro, y queda:
b(1 - 2a) = -a, divides por (1 - 2a) en ambos miembros, y queda:
b = -a/(1 - 2a),
y observa que debe cumplirse que el denominador no tome el valor cero, de donde tienes que la incógnita a no puede tomar el valor 1/2.
Espero haberte ayudado.
-
Porfavor, si alguien pudiese explicarme como debo plantear el siguiente ejercicio.
1) Estudia el rango de M (matriz) en función de los valores del parámetro "a" :
M= 2 1 0 1
a 2 -1 0
1 -1 a+2 8


Antonio Silvio Palmitano
el 2/10/19Vamos con una orientación.
Observa que tienes una matriz con tres filas y cuatro columnas, por lo que su rango es menor o igual que 3.
Observa que la submatriz formada por los dos últimos elementos de las dos primeras filas tiene determinante igual a 1 (que es distinto a cero),
por lo que tienes que el rango de la matriz de tu enunciado es como mínimo igual a dos.
Luego, queda que plantees los determinantes de las cuatro submatrices de orden tres que puedes formar (con las tres primeras columnas, con las dos primeras columnas y la tercera, con las dos primeras columnas y la cuarta, y con las tres últimas columnas), los desarrolles, y encuentres los valores de la indeterminada (a) que los hacen iguales a cero;
luego, tienes dos posibilidades:
1°)
si algún o algunos valores anulan los cuatro determinantes a la vez, entonces tienes para ellos que el rango de la matriz es igual a dos;
2°)
si ningún valor anula a los cuatro determinantes a la vez, entonces tienes que el rango de la matriz es igual a tres.
Espero haberte ayudado.