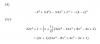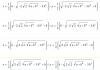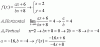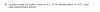-
Hola, alguien podría ayudarme con éstas preguntas? en la pregunta de resolver el sistema de ecuaciones lineales no se que hacer luego de realizar el a.x+b.y=c, y en la pregunta de determinar la distancia euclídea me da raíz de 39 y no aparece en las opciones, la que dice "determinar cuál ha de ser el valor del componente
para que ambos vectores sean ortogonales" ya la hice, pero tengo mis dudas en las otras 2. Gracias por su colaboración.
-
El sustraendo no es de grado 1?. Si se hace la división de ese sustraendo resultaría un polinomio de grado 1 no?. Mil gracias

Breaking Vlad
el 25/9/19Antonio Silvio Palmitano
el 25/9/19Recuerda que las palabras "minuendo" y "sustraendo" corresponden a una resta, por ejemplo, si tienes la resta:
a - b,
entonces tienes que a es el minuendo, y b es el sustraendo;
y con respecto al argumento del límite de tu primer ejercicio, entonces tienes que:
el minuendo es √(x3-5x), y
el sustraendo es (3x2-7x+2)/(2x-1).
Luego, si te refieres solo a la expresión del segundo término del argumento, observa que tienes expresada una división de polinomios en forma fraccionaria, por lo que tienes que el numerador o "dividendo" es (3x2-7x+2), y que el denominador o "divisor" es (2x-1).
Espero haberte ayudado.
-
Si:
u=i - 2j +3kv=3i +j -4k
Como se calcula u x v?
Antonio Silvio Palmitano
el 25/9/19Recuerda la expresión general del desarrollo de un producto vectorial:
u x v = < a , b , c > x < x , y , z > = < bz-cy , -az+cx , ay-bx >.
Luego, observa que para el vector u = i - 2j + 3k = < 1 , -2 , 3 > de tu enunciado tienes: a = 1, b = -2, c = 3;
y que para el vector v = 3i + j - 4k = < 3 , 1 , -4 > tienes: x = 3, y = 1, z = -4;
luego, planteas el producto vectorial, reemplazas los valores de las coordenadas en la expresión vectorial remarcada, y queda:
u x v = < (-2)(-4)-(3)(1) , -(1)(-4)+(3)(3) , (1)(1)-(-2)(3) > = < 8-3 , 4+9 , 1+6 > = < 5 , 13 , 7 >.
Espero haberte ayudado.
-
Buenas, tengo dudas en el ejercicio 24. Creo que se tiene que hacer por el teorema de bolzano, pero aún así no consigo sacarlo. Muchas gracias. Es f(xo)= xo
Pablo
el 25/9/19Antonio Silvio Palmitano
el 25/9/1924)
Tienes la expresión de la función:
f(x) = sen(x)/2 + π (1),
y observa que el dominio de la función es el conjunto de los números reales.
Luego, planteas la expresión de una nueva función:
g(x) = f(x) - x (*), sustituyes la expresión señalada (1), y queda:
g(x) = sen(x)/2 + π - x (2),
y observa que esta nueva función es continua en todo su dominio, que es el conjunto de los números reales.
Luego, derivas la expresión señalada (2), y queda:
g'(x) = cos(x)/2 - 1,
observa que la función derivada está definida en todo el dominio de la función, y observa además que la función derivada toma valores negativos para todo valor real, ya que el primer término de su expresión toma valores comprendidos entre -1/2 y 1/2, por lo que la función derivada toma valores comprendidos entre -3/2 y - 1/2; y para mostrar todo esto con más rigor, puedes plantear la inecuación doble:
-1 ≤ cos(x) ≤ 1, divides por 2 en los tres miembros (observa que no cambian las desigualdades), y queda:
-1/2 ≤ cos(x)/2 ≤ 1/2, restas 1 en los tres miembros, y queda:
-3/2 ≤ cos(x)/2 - 1 ≤ -1/2;
luego, como tienes que la función derivada de la función g toma valores estrictamente negativos para todo valor real, entonces tienes que la función g es estrictamente decreciente, y como además es continua y derivable en todo el conjunto de los números reales, entonces tienes también que es inyectiva y, por lo tanto, toma valores distintos para distintos números reales de su dominio;
luego, puedes plantear que existe un único valor x0 perteneciente al conjunto de los números reales, para el que se cumple la condición:
g(x0) = 0, sustituyes la expresión señalada (*) evaluada, y queda:
f(x0) - x0 = 0, sumas x0 en ambos miembros, y queda:
f(x0) = x0.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 25/9/19Puedes llamar N a la cantidad de pasajeros, y puedes llamar C al costo del viaje.
Luego, tienes la primera situación: "si cada pasajero paga $ 3100, faltan $ 300", por lo que puedes plantear la ecuación:
C - 300 = 3100*N, aquí sumas 300 en ambos miembros, y queda:
C = 3100*N + 300 (1).
Luego, tienes la segunda situación: "si cada pasajero paga $ 3200, sobran $ 100", por lo que puedes plantear la ecuación:
C + 100 = 3200*N, aquí sustituyes la expresión señalada (1) en el primer término, y queda:
3100*N + 300 + 100 = 3200*N, reduces términos semejantes en el primer miembro, y queda:
3100*N + 400 = 3200*N, divides por 100 en todos los términos, y queda:
31*N + 4 = 32*N, restas 32*N y restas 4 en ambos miembros, y queda:
-N = -4, multiplicas por -1 en ambos miembros, y queda:
N = 4 pasajeros;
luego, reemplazas este valor remarcado en la ecuación señalada (1), y queda:
C = 3100*4 + 300, resuelves, y queda:
C = $ 12700.
Espero haberte ayudado.