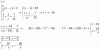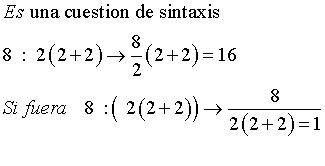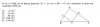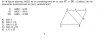-
Buenas, tengo duda de cómo resolver un ejerció.

La ley que hallé es F=√(16t).
Lo que pienso es integrar la aceleración para hallar la velocidad , y luego parametrizar . Pero no sé si está bien de esa forma


Antonio Silvio Palmitano
el 3/8/19Tienes los datos:
F(t) = √(16*t) = 4*√(t) = 4*t1/2 (expresión de la fuerza aplicada en función del tiempo, válida para t ≥ 0, expresada en Newtons),
M = 2 gr = 0,002 Kg (masa de la esferita).
v(0) = 0 (condición inicial para la velocidad, expresada en m/s),
x(0) = x0 (condición inicial para la posición, expresada en metros).
a)
Tienes la expresión de la aceleración:
a(t) = F(t)/M, sustituyes expresiones, y queda:
a(t) = 4*t1/2/0,002, resuelves el coeficiente, y queda:
a(t) = 2000*t1/2 (expresión de la aceleración en función del tiempo, expresada en m/s2).
b)
Planteas la expresión de la aceleración en función de la velocidad y del tiempo, y queda:
dv/dt = a(t), sustituyes la expresión de la aceleración, y queda:
dv/dt = 2000*t1/2, separas variables, y queda:
dv = 2000*t1/2*dt, integras en ambos miembros, y queda:
v(t) = (4000/3)*t3/2 + C (1), que es la expresión general de la velocidad en función del tiempo;
luego, planteas la condición inicial para la velocidad:
v(0) = 0, sustituyes la expresión señalada (1) evaluada en el primer miembro, cancelas el término nulo, y queda:
C = 0, reemplazas este valor en la expresión señalada (1), cancelas el término nulo, y queda:
v(t) = (4000/3)*t3/2, que es la expresión de la velocidad en función del tiempo para este problema.
c)
Planteas la expresión de la velocidad en función de la velocidad y del tiempo, y queda:
dx/dt = v(t), sustituyes la expresión de la velocidad que tienes remarcada, y queda:
dx/dt = (4000/3)*t3/2, separas variables, y queda:
dx = (4000/3)*t3/2*dt, integras en ambos miembros, y queda:
x(t) = (8000/15)*t5/2 + D (3), que es la expresión general de la posición en función del tiempo;
luego, planteas la condición inicial para la posición:
x(0) = x0, sustituyes la expresión señalada (1) evaluada en el primer miembro, cancelas el término nulo, y queda:
D = x0, reemplazas esta expresión en la expresión señalada (3), y queda:
x(t) = (8000/15)*t5/2 + x0, que es la expresión de la posición en función del tiempo para este problema.
Debes considerar las unidades y datos que tengas en el enunciado completo del problema, lo que puede conducir a algunos cambios en los coeficientes de las funciones aceleración, velocidad y posición, pero ten en cuenta que el procedimiento que te hemos mostrado es correcto.
Espero haberte ayudado.
-
-
 La respuesta es cada una por si sola pero segun yo solo tengo en comun el angulo de 90º,mediante que teoremas sale el otro angulo o los otros angulos,?MUCHAS GRACIAS
La respuesta es cada una por si sola pero segun yo solo tengo en comun el angulo de 90º,mediante que teoremas sale el otro angulo o los otros angulos,?MUCHAS GRACIAS

David
el 14/10/19Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
No consigo resolver este problema. Halla dos números naturales sabiendo que la quinta parte de su diferencia es 2 y la suma de sus inversos es 7/12.


Antonio Silvio Palmitano
el 2/8/19Comienza por designar con x e y a los números naturales buscados.
Luego, tienes que "la quinta parte de su diferencia es 2", por lo que puedes plantear la ecuación:
(1/5)*(x - y) = 2, multiplicas por 5 en ambos miembros, y queda:
x - y = 10, sumas y en ambos miembros, y queda:
x = 10 + y (1).
Luego, tienes que "la suma de sus inversos es 7/12, por lo que puedes plantear la ecuación:
1/x + 1/y = 7/12, multiplicas por 12xy en todos los términos, simplificas, y queda:
12y + 12x = 7xy (2).
Luego, sustituyes la expresión señalada (1) en el segundo término del primer miembro y en el último factor del segundo miembro de la ecuación señalada (2), y queda:
12y + 12(10 + y) = 7(10 + y)y, distribuyes el segundo término del primer miembro, distribuyes el segundo miembro, y queda:
12y + 120 + 12y = 70y + 7y2, reduces términos semejantes en el primer miembro, y queda:
24y + 120 = 70y + 7y2, restas 7y2 y restas 70y en ambos miembros, y queda:
-7y2 - 46y + 120 = 0, multiplicas en todos los términos por -1, y queda:
7y2 + 46y - 120 = 0,
que es una ecuación polinómica cuadrática, cuyas soluciones son:
1º)
y = (-46 - 74)/14 = -120/14 = - 60/7, que no es un número natural;
2º)
y = (-46 + 74)/14 = 28/14 = 2, que sí es un número natural,
reemplazas este valor en la ecuación señalada (1), y queda:
x = 10 + 2 = 12, que es otro número natural.
Luego, tienes que la solución de este problema es: x = 12, y = 2,
y puedes comprobar que se verifican las ecuaciones señaladas (1) (2) para esta solución (te dejo la tarea).
Espero haberte ayudado.
-
Hola! Necesito ayuda en el siguiente ejercicio. Halla el valor de m para que el polinomio P(x)= mx3 - 6x2 - 4x +8 tenga 2 por raíz.


Antonio Silvio Palmitano
el 2/8/19Aquí aplicas el Teorema del Resto (observa que 2 es una raíz del polinomio), y tienes:
P(2) = 0, sustituyes la expresión evaluada del polinomio en el primer miembro, y queda:
m*23 - 6*22 - 4*2 + 8 = 0, resuelves los tres primeros términos, y queda:
8*m - 24 - 8 + 8 = 0, cancelas términos opuestos, sumas 24 en ambos miembros, y queda:
8*m = 24, divides por 8 en ambos miembros, y queda:
m = 3.
Luego, tienes que el polinomio cuya expresión es:
P(x) = 3*x3 - 6*x2 - 4*x + 8,
tiene como una de sus raíces a:
x1 = 2.
Espero haberte ayudado.
-
Hola, qué tal? Los molesto para ver si me pueden ayudar. No puedo identificar a qué cónica pertenece la ecuación. Es que si completo cuadrados me queda = -1 y allí me trabo.
Gracias por adelantado. Saludos!


Antonio Silvio Palmitano
el 2/8/19Vamos con una precisión.
Tienes la expresión de la función, cuyo dominio es D = R2:
f(x,y) = x2 - 2x + y2 - 2y + 3,
sumas y restas 1, y queda:
f(x,y) = x2 - 2x + 1 - 1 + y2 - 2y + 3,
factorizas el trinomio cuadrado perfecto, y queda:
f(x,y) = (x - 1)2 - 1 + y2 - 2y + 3,
sumas y restas 1, y queda:
f(x,y) = (x - 1)2 - 1 + y2 - 2y + 1 - 1 + 3,
factorizas el trinomio cuadrado perfecto, y queda:
f(x,y) = (x - 1)2 - 1 + (y - 1)2 - 1 + 3,
reduces términos numéricos, ordenas términos, y queda:
f(x,y) = (x - 1)2 + (y - 1)2 + 1 (1),
que es la expresión canónica de la función, cuya gráfica tiene la ecuación:
z = (x - 1)2 + (y - 1)2 + 1,
que corresponde a un paraboloide con eje de simetría paralelo al eje coordenado OZ y que se extiende hacia valores positivos del eje OZ, cuyo vértice es el punto V(1,1,1), que corresponde a un mínimo absoluto de la función.
Luego, planteas la ecuación general de las curvas de nivel de la función, y queda:
f(x,y) = k, con k ∈ R,
sustituyes la expresión de la función señalada (1) en el primer miembro, y queda:
(x - 1)2 + (y - 1)2 + 1 = k,
restas 1 en ambos miembros, y queda:
(x - 1)2 + (y - 1)2 = k - 1 (2),
que es la ecuación general de las curvas de nivel de la función,
y observa que corresponde a una familia de circunferencias concéntricas,
cuyo centro es el punto C(1,1),
y cuyos radios tienen la expresión general: Rk = √(k - 1),
y aquí tienes que debe cumplirse la condición: k - 1 ≥ 0, aquí sumas 1 en ambos miembros, y queda:
k ≥ 1, de donde tienes que la imagen de la función es el intervalo I = [1,+∞).
Luego, tienes la ecuación de la curva en estudio en tu enunciado (observa que se trata de una circunferencia con centro C(1,1) y radio Rk = 2):
(x - 1)2 + (y - 1)2 = 4,
comparas término a término con la ecuación general de las curvas de nivel de la función señalada (2), observa que los primeros miembros de estas ecuaciones coinciden término a término, por lo que tienes que los segundos miembros deben ser iguales, por lo que puedes plantear la ecuación:
k - 1 = 4,
sumas 1 en ambos miembros, y queda:
k = 5,
que es un valor perteneciente a la imagen de la función;
luego, puedes concluir que la circunferencia cuya ecuación cartesiana canónica es: (x - 1)2 + (y - 1)2 = 4 es una curva de nivel de la función,
cuyos puntos pertenecen todos al dominio de la misma, y ésta toma el valor k = 5 para todos ellos.
Espero haberte ayudado.
-
Estaba en facebook y ví un post controversial sobre cuál es el resultado de 8 : 2(2+2), según unicoos es 16, pero esta pregunta no puede replantearse como
8
_______
2(2+2)
? O solo se puede hacer esto en ecuaciones con incógnitas?
-


Alejandro Legaspe
el 2/8/19Observa que al ser ADEF un cuadrado,entonces el angulo EFD es de 90°,entonces los angulos EFB y DFC deben de sumar 90°,asi,como la suma de los angulos del triangulo BEF debe ser 90°,debe de ocurrir que el angulo EBF=DFC y razonando analogamente para el triangulo DFC se tiene que el angulo DFC=DCF
Ahora bien,como los angulos EBF y DFC son iguales,entonces aplicando la función seno,haciendo uso de los triangulos EBF y FDC respectivamente,tenemos que
EF/BF=DC/FC...(1)
Observa que como AEDF Es cuadrado entonces EF=FD=DA=AE,para simplificar usemos x como el lado del cuadrado AEDF,asi x=EF=FD=DA=AE,ademas AC=AD+DC=x+DC
Sabiendo que AC=15cm, de (1),tenemos entonces que
x/BF=((15-x)/FC
Asi,se tiene que
FC x= BF(15-x)
BFx +FC x =BF 15
(BF+FC)x=BF (15)
BC x=BF (15)
x=(BF/BC)15
Para obtener BF observa el triangulo BEF,por el teorema de pitágoras,y observando que AB=AE+EB=x+EB,sabemos que,como AB=10cm
BF=√((10-x)²+x²)=√(2x²-20x+100)
Ademas,del triangulo ABC,sabemos que,por el teorema de pitágoras
BC=√(15²+10²)=5√13
Asi,entonces tenemos que
x=(BF/BC)15=(15√(2x²-20x+100))/ (5√13)
Elevando al cuadrado,entonces
x²=9(2x²-20x+100)/13
13x²=18x²-180x+900
5x²-180x+900=0
x²-36x+180=0
Asi,tenemos que x es
x=(36±√(1296-720)) / 2 =(36±√576)/2=(36±24)/2
Asi,se tiene dos soluciones,a saber x=30 y x=6,observa que como AC=x+DC es claro que x<AC=15cm,asi pues,tenemos que x=6cm
Por lo que el area del cuadrado ADEF es 36cm²
-


Alejandro Legaspe
el 2/8/19Obs: la notacion ang quiere decir angulo
Para ver que I es cierta,observa que si trazamos una paralela a AB que pase por E,siendo G el punto de interseccion de esta recta con AD,entonces el angulo ABD=FEG...(1)
ademas como GE es paralela a AB por construccion y AB es paralela a DC por ser ABCD paralelogramo,entonces GE es paralela a DC,asi FE es una recta que pasa por dos paralelas,asi pues por ser angulos alternos internos,tenemos que el angulo FEG y el angulo EFC son iguales, y por (1),entonces tenemos quelos angulos ABD y EFC son iguales.
Para ver que el angulo DAB es igual al angulo FCE se tiene por ser ABCD paralelogramo,pues siempre los angulos internos opuestos son iguales,asi pues con esta afirmacion podemos decir que el angulo FEC y el angulo ADB son iguales,pues como FE es paralela a DB Y BC es una recta que corta a ambas,entonces el angulo FEC es igual al angulo DBE,asi pues notamos que angABC=angABD +angDBE=angABD+andFEC,por otro lado,como DB es paralela a FE y DC es una recta que corta a mbas,entonces angCFE=angCDB,observa ademas que angADC=angADB+angCDB
Asi pues como los angulos opuestos del paralelogramo ABCD son iguales,entonces
angADC=angABC
angADB+angCDB=angABD+angDBE
Como angABD=angCFE=angCDB entonces,tenemos que angADB=angDBE=angFEC
Asi los angulos internos de los triangulos ADB y FEC son iguales entonces son semejantes.
Para la 2,pienso que si es verdad pues el angFEC lo tienen en comun,y como DB es paralela a FE y DC corta a ambas,entonces angCDB=angCFE,ahora bien,como CB corta a FE y DB al ser estas paralelas,entonces angCEF=angCBD
Asi,los angulos son iguales entre ambos triangulos,es decir,son semejantes.
Y la 3 sale de las otras dos,pues como el triangulo ABD es semejante con el triangulo CFE (Por I)y este ultimo es semejante con el triangulo BDC (Por ii)
entonces ocurre que el triangulo ABD es semejante con el trianguo BDC,asi la respuesta seria la E
-
Buenas Unicoos! Por favor, Me ayudan con éstos ejercicios de optimizacion..necesito entender como se plantean. Gracias



Antonio Silvio Palmitano
el 2/8/19a)
Puedes plantear la expresión general del punto B, que pertenece al arco de la parábola, y queda: B( b , (b-3)2 ) (1),
y observa que debe verificarse la doble inecuación: 3 ≤ b ≤ 6 (2).
Luego, tienes que la pendiente de la recta que pasa por el punto A(6,0) y por el punto B queda expresada: m = (b-3)2/(b-6),
luego, con las coordenadas del punto A, y con la expresión de la pendiente de la recta, planteas su ecuación cartesiana explícita, y queda:
y = ( (b-3)2/(b-6) )*(x - 6) (3),
que es la ecuación cartesiana explícita de la recta que contiene al lado AB, que es el primer lado del triángulo.
Luego, tienes que el eje OX contiene al segundo lado del triángulo, por lo que planteas la ecuación cartesiana de dicho eje, y queda:
y = 0 (4).
Luego, planteas la ecuación de la recta perpendicular al eje OX que pasa por el punto B (observa que esta es paralela al eje OY, y que contiene al tercer lado del triángulo), y queda:
x = b (5).
Luego, tienes que el primer vértice del triángulo es el punto: A, que el segundo vértice es el punto B, y para plantear la expresión del tercer vértice, planteas la intersección de las rectas que contienen al segundo y al tercer lado respectivamente, y tienes que el tercer vértice tiene la expresión: C(b,0), y observa que este último vértice corresponde al ángulo recto del triángulo.
Luego, observa que las rectas que contienen al segundo y al tercer lado del triángulo son perpendiculares, por lo que tienes que los catetos del triángulo son los segmentos CA y CB, cuyas longitudes quedan expresadas:
│CA│ = √( (6-b)2 + (0-0)2 ) = √( (6-b)2 ) = 6 - b (6),
│CB│ = √( (b-b)2 + ( (b-3)2-0 )2 ) = √( (b-3)4 ) = (b - 3)2 (7).
Luego, planteas la expresión del área del triángulo rectángulo en función de las longitudes de sus catetos, y queda:
A = (1/2)*│CA│*│CB│, sustituyes las expresiones señaladas (6) (7), y queda la expresión de la función:
A(b) = (1/2)*(6 - b)*(b - 3)2 (8),
que corresponde al área de los posibles triángulos rectángulos.
Luego, derivas la expresión de la función señalada (8) (observa que debes aplicar la Regla de la Multiplicación de Funciones), y queda:
A'(b) = -(1/2)*(b - 3)2 + (6 - b)*(b - 3), extraes factor común, y queda:
A'(b) = (b - 3)*( -(1/2)*(b - 3) + (6 - b) ), resuelves el segundo factor de esta expresión, y queda:
A'(b) = (b - 3)*(-(3/2)*b + 15/2) (9).
Luego, planteas la condición de valor estacionario (posible máximo o posible mínimo de la función), y queda:
A'(b) = 0, sustituyes la expresión señalada (9) en el primer miembro, y queda:
(b - 3)*(-(3/2)*b + 15/2) = 0, y por anulación de una multiplicación de expresiones, tienes dos opciones:
1º)
b - 3 = 0, aquí sumas 3 en ambos miembros, y queda: b = 3,
reemplazas este valor en las expresiones de los vértices B y C, resuelves, y queda: B(3,0) y C(3,0),
y como estas dos expresiones coinciden, tienes que este valor no corresponde a una solución para este problema, ya que tienes como solución al segmento que une los puntos (3,0) y (6,0);
2º)
-(3/2)*b + 15/2 = 0, aquí multiplicas por -2/3 en todos los términos, y queda:
b - 5 = 0, aquí sumas 5 en ambos miembros, y queda: b = 5, que cumple la condición señalada (2),
reemplazas este valor remarcado en las expresiones de los vértices B y C, resuelves, y queda: B(5,4) y C(5,0),
y observa que con estos dos punto y con el punto A(6,0) tienes un triángulo rectángulo en el punto C.
Te dejo la tarea de hacer el gráfico cartesiano.
Espero haberte ayudado.


Antonio Silvio Palmitano
el 2/8/19b)
Vamos por una orientación.
Puedes designar con x al ancho y al largo de la base, y con y a la altura del depósito, que es un prisma rectangular recto con base cuadrada, y observa que los valores de x e y deben ser estrictamente positivos.
Luego, planteas la expresión del volumen del depósito, y queda:
V(x,y) = x2*y, y como tienes el valor del volumen del depósito en tu enunciado, puedes plantear la ecuación:
x2*y = 500 (en litros), y aquí divides por x2 en ambos miembros, y queda:
y = 500/x2 (1).
Luego, planteas la expresión del área de la base del depósito, y queda:
Ab = x2 (2).
Luego, planteas la expresión del área total de las cuatro paredes rectangulares del depósito, y queda:
Atp = 4*x*y (3).
Luego, planteas la expresión del área total (base más paredes), y queda:
AT = Ab + Atp, sustituyes las expresiones señaladas (2) (3), y queda la expresión:
AT = x2 + 4*x*y;
luego, sustituyes la expresión señalada (1) en el último término, resuelves su coeficiente, simplificas, y queda:
AT = x2 + 2000/x (4),
que es la expresión del área total del depósito en función de la longitud del lado de su base cuadrada.
Luego, queda que plantees la expresión de la derivada primera, iguales a cero a fin de determinar los valores estacionarios (recuerda que debes considerar los valore estrictamente positivos), y luego continuar (te dejo la tarea).
Espero haberte ayudado.