-


Antonio Silvio Palmitano
el 15/3/19Tienes el argumento del límite:
f(x) = 1/(x-1) - x/(x2-1), factorizas el denominador del segundo término, y queda:
f(x) = 1/(x-1) - x / (x+1)(x-1), extraes denominador común, y queda:
f(x) = ( x+1 - x ) / (x+1)(x-1), cancelas términos opuestos en el numerador, y queda:
f(x) = 1 / (x+1)(x-1) (1).
Luego, como tienes que x tiende a 1 desde valores mayores que 1 (o sea "por la derecha"), observa que el primer factor del denominador tiende a 2 y que el segundo factor tiende a 0 desde valores positivos;
luego, tienes que el denominador tiende a 0 desde valores positivos,
y como el numerador es constante, distinto de cero y positivo,
puedes concluir que el el argumento del límite tiende a +infinito:
Lím(x→1+) ( 1/(x-1) - x/(x2-1) ) = sustituyes la expresión señalada (1), y queda:
= Lím(x→1+) ( 1 / (x+1)(x-1) ) = +∞.
Espero haberte ayudado.
-
Buenas noches,¿
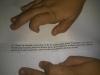
me podría responder algún profesor indicándome cuál sería su respuesta mejor valorada a las preguntas que planteo en la imagen adjunta?



Antonius Benedictus
el 15/3/191) Porque la función no es derivable en x=0, al no coincidir la derivada por la derecha con la derivada por la izquierda.
2) Ves que la derivada por la izquierda (al sustituir) es -4 y por al derecha es 4. Al tratarse de funciones continuas y derivables no es estrictamente necesario que utilices la definición de la derivada.