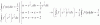-
Calcular δ/δs (f o g)(1,0) si f y g son las siguientes:
f(u,v) = cos(u)sen(v)
g(s,t) = cos[(t2·s) , ln(√(1+s2)]
César
el 26/2/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
¿Me podrían decir cómo resuelvo este problema de sistemas?
Un comerciante compró 500 envases de leche, 200 de zumo de fruta y 50 paquetes de café, y pagó 640€ en total.
Cierto tiempo después había vendido la leche, ganando un 30%; el zumo de fruta, ganando un 20% y el café, perdiendo un 10%. Por todo ello obtuvo 768 €.
Sabiendo que el precio de compra de cada envase de zumo fue el 60% del precio de compra de cada paquete de café, ¿cuáles fueron los precios de compra y de venta de cada uno de los tres productos?
Mauro
el 26/2/18Hola Cristina te ayudo
acabo de plantearlo
L= precio de venta envases de leche
Z= precio de venta zumos
C=precio de venta paquetes de café
Primera ecuación de compra
500L + 200Z + 50C = 640
Segunda ecuación de venta
(500L + 500L*0,30)+(200Z + 200Z*0,20)+(50C - 50C*0,10)= 768
Relación de precios
Z=0,6C
A partir de ahí te saldrá
A mi me salió precio del café = 2€
Saludos desde Boli
-
Antonio Silvio Palmitano
el 26/2/18Plantea la sustitución (cambio de variable):
u = ex/2, de donde tienes: du = ex/2*dx/2 = (1/2)*ex/2*dx, y observa que los límites de integración quedan: u(0) = 1, u(2) = e;
luego sustituyes, y la integral queda:
I = 1∫e f(u)*(1/2)*du = 1∫e f(u)*(1/2)*du = (1/2) * 1∫e f(u)*du = reemplazas = (1/2)*(1/2) = 1/4.
Espero haberte ayudado.
-
Hola! Alguien me puede ayudar con este problema?
Una empresa que fabrica cosméticos para el cabello, envasa el 40% del champú en la planta I y el resto en la planta II. En el llenado, que se realiza automáticamente en ambas plantas, el contenido es inferior al estipulado un 3% de las veces para la planta I y un 2,5% para la II. Si se extrae al azar un envase de la producción, ¿cuál es la distribución Bernouilli en relación al suceso: “envase con contenido impropio”?
-
Facundo Soria
el 26/2/18
Ángel
el 27/2/18Observa que la x no puede tomar ningún valor entre en el intervalo (-inf, -1) , debido a que haría que la raíz fuera negativa, y por lo tanto fuera del dominio de los reales.
Tampoco puede tomar el valor x= -1 porque f(-1)=1/√0 = 1/0 y eso es una indeterminación, por lo que también lo descartamos.
Tampoco puede tomar el valor x=0, porque f(0)= (1-1)/0 = 0/0 , que tampoco está definido en los números reales.
**Para cualquier otro valor de x en f(x), excepto los remarcados en las líneas anteriores, la función SÍ está definida, por lo que el Dominio= (-1,0) U (0,inf) , o equivalentemente ℛ - { (-inf, -1) U {-1} U {0} }
-
Antonio
el 26/2/18
-
Buenas tardes, ¿me podrían ayudar con estas integrales? :
- ∫ sinx · ecosx dx
- Área de la región limitada por f(x) = x2 - 4x + 5, su recta tangente a x=3 y los semiejes positivos.
Muchas gracias.
-
Antonius Benedictus
el 26/2/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).