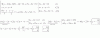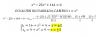-
A la hora de demostrar por inducción si no me cumple para " N=1" ni para "N=2" ni "N=3" ........ Pues qué tengo que hacer? Y si solo cumple para ",N=1" no cumple para los de más.. en este caso?
Antonio Silvio Palmitano
el 4/1/18Vamos con una orientación.
Recuerda el enunciado del Principio de Inducción (5° axioma de Peano):
Si la proposición es Verdadera para el primer elemento, y,
si aceptas que la proposición es Verdadera para un elemento general entonces es Verdadera para el elemento general siguiente;
entonces la proposición es Verdadera para todo número natural, a partir del primer elemento en adelante.
Por lo tanto:
- si la proposición es falsa para n = 1, tienes que es Falsa;
- si la proposición es falsa para algún natural, el que sea, tienes que es Falsa;
y no tienes más nada que demostrar.
Recuerda que para demostrar que la proposición es Verdadera debes completar todos los pasos del Método de Inducción, y si uno de ellos no se cumple, tienes que la proposición es Falsa.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 3/1/18Tienes la proposición:
P(n):
n! > 2n-1, con n ∈ N, n > 2 (observa que el primer elemento es n = 3).
Luego, plantea:
1°)
P(3):
Para n = 3, tienes:
3! > 23-1 es Verdadera, ya que el primer miembro es 6 y el segundo miembro es 4.
2°)
P(h):
h! > 2h-1, con h ∈ N, h > 2 (Hipótesis Inductiva, que aceptas como Verdadera).
3°)
P(h+1):
(h+1)! > 2h+1-1 = 2h (Tesis Inductiva, que debes demostrar que es Verdadera).
4°)
Demostración:
(h+1)! = (h+1)*h! > (aplicas la Hipótesis Inductiva) > (h+1)*2h-1 > (recuerda que h es mayor que 2) > (2+1)*2h-1 =
= 3*2h-1 > 2*2h-1 = 21+h-1 = 2h;
luego, por la cadena de desigualdades e igualdades puedes concluir:
(h+1)! > 2h es Verdadera.
5°)
Conclusión:
P(3) es Verdadera,
P(h) → P(h+1) es Verdadera,
por lo tanto puedes concluir, por el 5° Axioma de Peano (Principio de Inducción), que la proposición de tu enunciado es Verdadera.
Espero haberte ayudado.
-
Hola unicoos como podria hacer este ejercicio de ecuaciones bicuadradas? No logro entender como se hacen
x4 -25x2 mas 144 igual a 0.
GRACIAS UNICOOS
-
Antonius Benedictus
el 3/1/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Me lo explica alguien paso a paso
Opera y simplifica
[(x²-1/2x²-8)•(x-2/x-1)]÷x/x²+2x
Axel Morales Piñón.
el 3/1/18Antonio Silvio Palmitano
el 4/1/18Vamos con un ejemplo a modo de orientación, y comparto la indicación del colega Axel con respecto a que hagas buen uso de la notación, y, en todo caso, sería conveniente que envíes una foto del enunciado, a fin de evitar confusiones.
Si tienes en el enunciado:
F(x) = [ ( (x2-1) / (2x2-8) ) * ( (x-2) / (x-1) ) ] ÷ [ x / (x+2x) ];
comienza por factorizar en los numeradores y en los denominadores por separado:
x2-1 = (x+1)(x-1) (observa que es una resta de cuadrados perfectos),
2x2-8 = 2(x2-4) = 2(x+2)(x-2) (observa que tienes un factor común numérico, y luego una resta de cuadrados perfectos),
x2+2x = x(x+2) (observa que tienes un factor común literal);
luego, sustituyes, y la expresión de tu enunciado queda:
F(x) = [ ( (x+1)(x-1) / 2(x+2)(x-2) ) * ( (x-2)/(x-1) ] ÷ [ x / x(x+2) ];
simplificas los factores remarcados, y queda:
F(x) = [ ( (x+1)(x-1) / 2(x+2)(x-2) ) * ( (x-2)/(x-1) ] ÷ [ 1 / (x+2) ];
resuelves el producto entre expresiones algebraicas fraccionarias en el primer agrupamiento señalado entre corchetes, y queda:
F(x) = [ (x+1)(x-1)(x-2) / 2(x+2)(x-2)(x-1) ] ÷ [ 1 / (x+2) ];
simplificas los factores remarcados, y queda:
F(x) = [ (x+1) / 2(x+2) ] ÷ [ 1 / (x+2) ];
resuelves la división entre expresiones algebraicas fraccionarias, y queda:
F(x) = (x+1)(x+2) / 2(x+2);
simplificas los factores remarcados, y queda:
F(x) = (x+1)/2.
Espero haberte ayudado.