-
Hola, algien me podria resolver este problema porfavor
Una locomotora, que tiene una masa de 70000kg, arrastra por una via horizontal dos vagones de masas 20000kg y 10000kg respectivamente. Despreciando el rozamiento cpn la vía, calcula la fierza con la que actúa la locomotora y las tensiones entre los enganches de los vagones cuando arranca con una aceleración de 1,5 m/s².
Raúl RC
el 11/12/18El profe ya grabó un vídeo sobre este aspecto, lo viste?
https://www.youtube.com/watch?v=VwIMW5ggbAc
Ánimo!
-
Velocidad inicial y velocidad de escape no es lo mismo, no??
Antonio Silvio Palmitano
el 11/12/18Si se trata de disparar un cohete espacial, y consideras que el instante inicial es el del disparo, entoncies tienes que la velocidad inicial del cohete debe ser mayor o igual que la velocidad de escape, para que el móvil pueda vencer a la atracción gravitatoria terrestre.
Espero haberte ayudado
Francisco Javier Tinoco Tey
el 12/12/18Depende de la situación, Ya te digo que si la idea es lanzar un objeto desde la superficie terrestre para escapar de la atracción gravitatoria del planeta, ese cuerpo deberá partir de una velocidad inicial para recorrer un desplazamiento infinito.
Espero que te sirva, un saludo :)
-
En este ejercicio, en el apartado c, me piden que calcule la velocidad de una sonda espacial. Creo que se puede hacer de dos maneras: con la formula de la velocidad: raíz de (G*Mplaneta)/R, y también se puede hacer teniendo en cuenta el principio de conservación de la energía. Lo que pasa es que no da lo mismo con los dos métodos. Cual debo utilizar???

Antonio Silvio Palmitano
el 11/12/18a)
Tienes dos instantes especiales:
1°)
La sonda se encuentra muy cerca de la superficie del planeta, y se eleva con su velocidad de escape, por lo que su energía mecánica total queda expresada:
EM1 = EP1 + EC1 = -G*Mp*Ms/R + (1/2)*Ms*ve2 (1).
2°)
La sonda ha alcanzado un punto muy alejado del centro del planeta (R es muy grande, prácticamente es infinito), por lo que su energía potencial gravitatoria es prácticamente nula, y su velocidad también, por lo que su energía mecánica total queda expresada:
EM2 = EP2 + EC2 ≅ 0 (2).
Luego, como tienes que la energía mecánica se conserva (observa que despreciamos todo tipo de pérdida de energía), puedes plantear la ecuación:
EM1 = EM2,
sustituyes las expresiones señaladas (1) (2), y queda:
-G*Mp*Ms/R + (1/2)*Ms*ve2 ≅ 0,
multiplicas por 2*R en todos los términos de la ecuación, y queda:
-2*G*Mp*Ms + R*Ms*ve2 ≅ 0,
divides por Ms en todos los términos de la ecuación, y queda:
-2*G*Mp + R*ve2 ≅ 0,
sumas 2*G*Mp en ambos miembros, y queda:
R*ve2 ≅ 2*G*Mp,
divides por R en ambos miembros, y queda:
ve2 ≅ 2*G*Mp/R,
extraes raíz cuadrada en ambos miembros (observa que elegimos la raíz cuadrada positiva), y queda:
ve ≅ √(2*G*Mp/R),
que es la expresión del módulo de la velocidad de escape del planeta, y observa que depende solamente de su masa y de su radio).
b)
Planteas la expresión de la energía cinética inicial de la sonda, y queda:
(1/2)*Ms*vi2 = ECi,
multiplicas en ambos miembros por 2/vi2, y queda:
Ms = 2*ECi/vi2 (*),
que es el valor de la masa de la sonda.
Luego, establece un sistema de referencia con eje de posiciones Or con origen en el centro del planeta, y con dirección y sentido positivo acordes a la trayectoria de la nave. Luego, aplicas la Segunda Ley de Newton para el momento en el que la sonda recién se está desplazando luego del lanzamiento, y tienes la ecuación:
Ms*a = -G*Mp*Ms/R2,
divides en ambos miembros por Ms, y queda:
a = -G*Mp*Ms/R2,
que es el valor de la aceleración de la sonda, y observa que el signo negativo indica que su sentido es hacia el centro del planeta.
c)
Vamos con una orientación.
Observa que con la expresión de la energía mecánica inicial de la sonda señalada (1), y la expresión de la masa de la sonda remarcada y señalada (*) ya tienes todo lo que necesitas para calcular la energía mecánica inicial (EMi) de la sonda (te dejo la tarea).
Luego, observa que tienes que la altura de la sonda en el instante en estudio es: h = 600 Km = 6*105 m, y que tienes que determinar el módulo de su velocidad (vc), por lo que la expresión de su energía mecánica total queda:
EMc = EPc + ECc = -G*Mp*Ms/(R+h)2 + (1/2)*Ms*vc2.
Luego, solo queda que plantees conservación de la energía, y resuelvas la ecuación, cuya única incógnita es el módulo de la velocidad de la sonda en el instante en estudio (vc).
Haz el intento de terminar la tarea, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
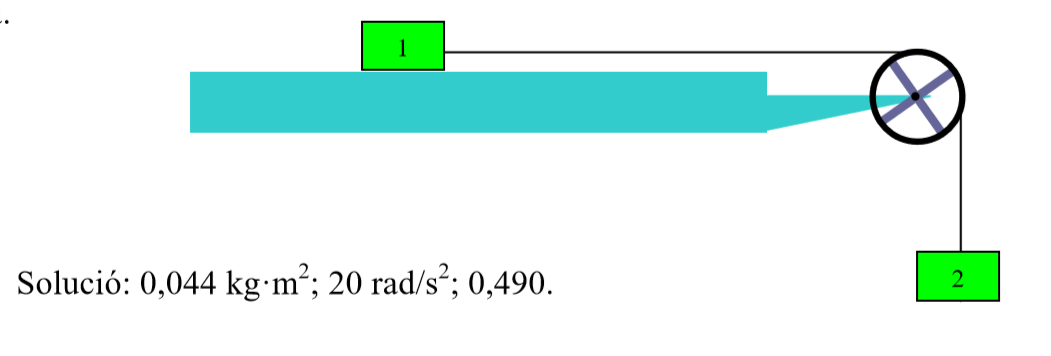
el 11/12/181)
Si consideras que la masa del bloque 1 es mayor que la masa del bloque 2: M1 > M2,
entonces tienes que el bloque 1 desciende, que el bloque 2 asciende, y que la polea gira con sentido antihorario.
Luego, observa que sobre el bloque 1 actúan dos fuerzas verticales, de las que indicamos sus módulos y sentidos:
Peso: P1 = M1*g, hacia abajo (favorable al sentido de desplazamiento de este bloque),
Tensión de la cuerda: T, hacia arriba (opuesto al sentido de desplazamiento de este bloque).
Luego, observa que sobre el bloque 2 actúan dos fuerzas verticales, de las que indicamos sus módulos y sentidos:
Peso: P2 = M2*g, hacia abajo (opuesto al sentido de desplazamiento de este bloque),
Tensión de la cuerda: T, hacia arriba (favorable al sentido de desplazamiento de este bloque).
Luego, establece un sistema de referencia con eje de posiciones OY vertical con sentido positivo hacia arriba, aplicas la Segunda Ley de Newton para ambos bloques, y tienes el sistema de ecuaciones:
-M1*g + T = -M1*a (observa que la aceleración tiene sentido negativo para el bloque 1),
-M2*g + T = +M2*a (observa que la aceleración tiene sentido positivo para el bloque 2);
luego, restas miembro a miembro la segunda ecuación con la primera, cancelas términos opuestos, y queda:
-M2*g + M1*g = M2*a + M1*a, ordenas términos y extraes factores comunes en ambos miembros, y queda:
(M1 - M2)*g = (M1 + M2)*a, divides en ambos miembros por (M1 + M2), y queda:
(M1 - M2)*g/(M1 + M2) = a, que es el valor del módulo de las aceleraciones de los bloques.
2)
Tienes dos instantes importantes (observa que consideramos que el origen de coordenadas se encuentra en un punto del eje OY ubicado muy por debajo de los dos bloques):
a)
Los bloques están en reposo, por lo que la energía cinética de ambos es igual a cero, su energía potencial es distinta de cero, y las expresiones de ambas energías quedan:
EPa = EP1a + EP2a = M1*g*y1a + M2*g*y2a,
ECa = 0.
b)
Los bloques están en movimiemtno, el bloque 1 ha descendido una altura Δh y su velocidad tiene módulo v y sentido negativo, y el bloque 2 a ascendido una altura Δh y su velocidad tiene módulo v y sentido positivo, y las expresiones de ambas energías quedan:
EPb = EP1b + EP2b = M1*g*(y1a - Δh) + M2*g*(y2a + Δh)
ECb = EC1b + EC2b = (1/2)*M1*v2 + (1/2)*M2*v2.
Luego, como tienes en tu enunciado que no intervienen fuerzas disipativas y que la polea y la cuerda son ideales, aplicas el Teorema de Conservación de la Energía y tienes que la variación de energía mecánica del sistema es igual a cero, por lo que tienes la ecuación:
ΔEMb = 0, expresas a la variación de energía mecánica en función de las variaciones de energía potencial y de energía cinética, y queda:
ΔEP + ΔEC = 0, expresas a las variaciones de energía en función de los valores iniciales y finales, y queda:
EPb - EPa + ECb - ECa = 0, cancelas el término nulo (ECa = 0), y queda:
EPb - EPa + ECb = 0, sumas EPa y restas EPb en ambos miembros, y queda:
ECb = EPa - EPb, sustituyes expresiones, y queda:
(1/2)*M1*v2 + (1/2)*M2*v2 = M1*g*y1a + M2*g*y2a - ( M1*g*(y1a - Δh) + M2*g*(y2a + Δh) ),extraes factores comunes en el primer miembro, distribuyes y resuelves signos en el segundo miembro, y queda:
(1/2)*(M1 + M2)*v2 = M1*g*y1a + M2*g*y2a - M1*g*(y1a + M1*g*Δh - M2*g*y2a - M2*g*Δh,
cancelas términos opuestos en el segundo miembro, y queda:
(1/2)*(M1 + M2)*v2 = M1*g*Δh - M2*g*Δh,
extraes factores comunes en el segundo miembro, y queda:
(1/2)*(M1 + M2)*v2 = (M1 - M2)*g*Δh,
multiplicas por 2 y divides por (M1 + M2) en ambos miembros, y queda:
v2 = 2*(M1 - M2)*g*Δh / (M1 + M2),
extraes raíz cuadrada en ambos miembros (observa que elegimos la raíz positiva), y queda:
v = √( 2*(M1 - M2)*g*Δh / (M1 + M2) ),
que es la expresión del módulo de las velocidades de los bloques.
c)
Planteas la expresión del impulso (cantidad de movimiento) total del sistema en función de las masas de los bloques y del módulo de sus velocidades (recuerda que consideramos que el sentido hacia arriba es positivo), y queda:
p = -M1*v + M2*v = (-M1 + M2)*v = -(M1 - M2)*v (*).
Luego, planteas la expresión del impulso total en función de la masa total del sistema y de la velocidad del centro de masas, y queda:
p = (M1 + M2)*Vcm (**).
Luego igualas las expresiones del impulso total señaladas (2) (1), y queda:
(M1 + M2)*Vcm = -(M1 - M2)*v,
divides por (M1 + M2) en ambos miembros, y queda:
Vcm = -(M1 - M2)*v / (M1 + M2),
que es la expresión de la velocidad del centro de masas del sistema, en función de las masas de los bloques y del módulo de sus velocidades.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 10/12/18Tienes los datos:
M = 200 g = 0,2 Kg (masa del oscilador),
A = 40 cm =0,4 m (amplitud de oscilación),
k = a determinar (constante elástica del resorte),
ω = a determinar (pulsación, o frecuencia angular de osicilación),
φ = a determinar (fase inicial),
U = 8 J (energía total del oscilador),
x(0) = -40 cm = -0,4 m (posición inicial del oscilador, en el instante inicial: ti = 0).
a)
Planteas la expresión de la energía total del oscilador en función de la constante elástica y de la amplitud de oscilación, y queda:
(1/2)*k*A2 = U, multiplicas en ambos miembros por 2/A2, y queda:
k = 2*U/A2, reemplazas datos, y queda:
k = 2*8/0,42, resuelves, y queda:
k = 100 N/m;
luego, planteas la expresión de la pulsación en función de la constante elástica y de la masa del oscilador, y queda:
ω = √(k/M), reemplazas datos, y queda:
ω = √(100/0,2), resuelves, y queda:
ω = √(500) rad/s;
luego, planteas la expresión general de la elongación de Movimiento Armónico Simple, y queda:
x(t) = A*sen(ω*t + φ) (1),
evalúas para el instante inicial, y queda:
x(0) = A*sen(ω*0 + φ), reemplazas datos, cancelas el término nulo en el argumento del seno, y queda:
-0,4 = 0,4*sen(φ), divides por 0,4 en ambos miembros, y queda:
-1 = sen(φ), compones en ambos miembros con la función inversa del seno, y queda:
-π/2 = φ;
luego, reemplazas este valor y los demás valores conocidos en la expresión de la elongación señalada (1), y queda:
x(t) = 0,4*sen(√(500)*t - π/2) (2).
Luego, derivas la expresión señalada (2) con respecto al tiempo, y la expresión de la velocidad del oscilador queda:
v(t) = 0,4*√(500)*cos(√(500)*t - π/2) (3);
luego, derivas la expresión señalada (3) con respecto al tiempo, y la expresión de la aceleración del oscilador queda:
a(t) = 0,4*( √(500) )2*( -sen(√(500)*t - π/2) ),
aquí resuelves el coeficiente, y queda:
a(t) = -200*sen(√(500)*t - π/2) (4).
Luego, para determinar el valor de la velocidad extrema, tienes a partir de la expresión señalada (3):
cos(√(500)*t - π/2) = ±1, compones en ambos miembros con la función inversa del coseno, y queda:
√(500)*t - π/2 = k*π con k ∈ Z, sumas π/2 en ambos miembros, y queda:
√(500)*t = k*π + π/2 con k ∈ Z, divides por √(500) en ambos miembros, y queda:
t = (k*π + π/2)/√(500) con k ∈ Z, que son los valores de los instantes en que la velocidad es extrema,
y observa que al reemplazarlos en la ecuación señalada (3) queda:
v( (k*π + π/2)/√(500) ) = ±0,4*√(500), que son los valores extremos de la velocidad, cuyo módulo queda:
vM = 0,4*√(500) m/s, que es el valor de la amplitud de velocidad del oscilador.
Luego, para determinar el valor de la aceleración extrema, tienes a partir de la expresión señalada (4):
sen(√(500)*t - π/2) = ±1, compones en ambos miembros con la función inversa del coseno, y queda:
√(500)*t - π/2 = m*π/2 con m ∈ Z, sumas π/2 en ambos miembros, y queda:
√(500)*t = m*π/2 + π/2 con m ∈ Z, divides por √(500) en ambos miembros, y queda:
t = (m*π/2 + π/2)/√(500) con m ∈ Z, que son los valores de los instantes en que la aceleración es extrema,
y observa que al reemplazarlos en la ecuación señalada (3) queda:
a( (m*π/2 + π/2)/√(500) ) = ±200, que son los valores extremos de la velocidad, cuyo módulo queda:
aM = 200 m/s2, que es el valor de la amplitud de aceleración del oscilador.
Espero haberte ayudado.
Raúl RC
el 10/12/18a) La constante del muelle se puede calcular a partir de la energía total, cuya expresión es:
Et=½·k·A2
siendo A=0,4 m
Con lo cual: k=2Et/A2=100 N/m
La ecuación del mas obedece a la expresión:
x(t)=Asen(ωt+φ0) obteniendo ω de la relación de dispersión k=mω2 por tanto:
ω=√(k/m)=√500 rad/s
Por otra parte si la elongación en el punto inicial es x(t=0)=-0,4 podemos hallar con esto la fase inicial que será:
-0,4=0,4sen(22,36·0+φ0) quedando sen(φ0)=-1=> φ0=270º=3π/2 rad
Finalmente la expresión del MAS:
x(t)=0,4sen(√500t+3π/2) m
b) la velocidad y aceleración se obtienen derivando la ecuación de posición del MAS respecto al tiempo:
v(t)= 0,4√500cos(√500t+3π/2) siendo vmax cuando el coseno vale uno, con lo cual:
vmax=0,4√500=8,94 m/s
En este caso el punto donde se alcanza la máxima velocidad se produce cuando x(t)=0 m, es decir, cuando la masa pasa justo por el origen
Respecto a la aceleración es la derivada de la velocidad:
a(t)=-0,4·500sen(√500t+3π/2) => siendo amax cuando el seno vale 1, con lo cual (en este caso utilizaremos el valor absoluto de la aceleración para despreciar el signo menos generado por la derivada, de esta manera hallamos el valor máximo y no el mínimo):
amax=0,4·500=200 m/s2
Teniendo en cuenta que el valor máximo de la aceleración se obtiene en el punto x(t)=0,4 m ,es decir, en el punto de mayor amplitud
Espero haberte ayudado ;)