-
Un viaja automóvil a 20 m/s y un camión a 16/ms. De manera simultanea, cada chófer ve que el otro vehículo viene hacia a el y frena de inmediato, con aceleración del automóvil es el doble que la del camión, determine la magnitud de la aceleración que debe tener el automóvil para que no se tope con el camión, considerando la distancia inicial de separación entre los dos carros al instante que frenan es de 300m.
Por favor ayuda
Gracias.
Antonio Silvio Palmitano
el 30/11/18Considera un sistema de referencia con eje de posiciones OX con dirección acorde al desplazamiento de los móviles, con sentido positivo acorde al desplazamiento del auto, con origen de coordenadas en la posición del auto cuando los conductores accionan los frenos, con instante inicial: ti = 0 correspondiente a dicho momento.
Luego, tienes los datos iniciales del auto:
xi = 0,
xf = a determinar,
vi = 20 m/s,
vf = 0,
aA = a determinar;
luego, planteas la ecuación posición-velocidad de Movimiento Rectilíneo Uniformemente Variado, y queda:
2*aA*(xf - xi) = vf2 - vi2, reemplazas datos, y queda:
2*aA*(xf - 0) = 02 - 202, resuelves operaciones numéricas, y queda:
2*aA*xf = -400, divides por 2 en ambos miembros, y queda:
aA*xf = -200 (1).
Luego, tienes los datos iniciales del camión:
xi = 300 m,
xf = a determinar,
vi = -16 m/s (recuerda que el sentido del desplazamiento del camión es opuesto al del auto),
vf = 0,
aC = -(1/2)*aA (2) (observa que el sentido de la aceleración del camión es opuesto a la del auto);
luego, planteas la ecuación posición-velocidad de Movimiento Rectilíneo Uniformemente Variado, y queda:
2*aC*(xf - xi) = vf2 - vi2, sustituyes expresiones y datos, y queda:
2*( -(1/2)*aA )*(xf - 300) = 02 - (-16)2, resuelves operaciones numéricas, y queda:
-aA*(xf - 300) = -256, multiplicas por (-1) en ambos miembros, y queda:
aA*(xf - 300) = 256 (3).
Luego, divides miembro a miembro entre las ecuaciones señaladas (1) (3), simplificas, y queda:
xf / (xf - 300) = -200/256, simplificas el segundo miembro, y queda:
xf / (xf - 300) = -25/32, multiplicas por 32*(xf - 300) en ambos miembros, y queda:
32*xf = -25*(xf - 300), distribuyes el segundo miembro, y queda:
32*xf = -25*xf + 7500, sumas 25*xf en ambos miembros, y queda:
57*xf = 7500, divides por 57 en ambos miembros, y queda:
xf = 2500/19 m ≅ 131,579 m;
luego, reemplazas este valor remarcado en la ecuación señalada (1), y queda:
aA*(2500/19) = -200, multiplicas en ambos miembros por 19/2500, y queda:
aA = -38/25 m/s2 = -1,52 m/s2;
luego, reemplazas este último valor remarcado en la ecuación señalada (2), y queda:
aC = -(1/2)*(-38/25), resuelves el segundo miembro, y queda:
aC = 19/25 m/s2 = 0,76 m/s2.
Espero haberte ayudado.
-
Hola buenas, les traigo este ejercicio de óptica geométrica:
Considere 3 ojos pertenecientes a 3 persoans de 20 años de edad (amplitud de acomodación de +10 dioptrias) y de estados refractivos diferentes, un emétrope, un miope 3D y un hipermétrope 3D. Para cada uno de ellos calcule el punto próximo, remoto y el recorrido de la acomodación.
Mi duda es, se como calcular el punto próximo del miope y del hipermétrope por la fórmula de la acomodación como AM=R-P donde R es la lente que en el caso del miope es -3D y P es el punto próximo, pero de ahí no se continuar con el problema, agradecería que me ayudaran
Muchas gracias de antemanoRaúl RC
el 2/12/18Lamento no poder ayudarte, pero de óptica solo tocamos aspectos relacionados con las expresiones que se ven en bachillerato, desde las ecuaciones de los espejos y/o lentes(distancia imagen, distancia objeto, distancia focal, etc) asi como el trazado de rayos correspondiente a óptica gométrica. Tu pregunta es propia de óptica fisiológica que se ve en la universidad, lo lamento de corazón
-
Hola chicos, voy un poco apurado y era para ver si me podrías resolver este pequeño problema de óptica geométrica:
Una persona tiene su punto próximo a 0.5 metros delante de sus ojos.
a) ¿Que potencia de lentes necesita para leer cómodamente a 0.25 metros?
Este apartado creo poder resolverlo como
1/s'-1/s = 1/f1/-0.5 -1/-0.25 = 1/f
1/f =2
b) ¿Donde estará su punto remoto con las lentes de cerca puestas?
Aqui tengo una duda, lo que haría sería esto y no se si es correcto
1/s'-1/s = 1/f
2=1/s' -1/infinito
s'=0
c) ¿Cuál es la acomodación utilizada?
AV = 1/dist punto próximo - 1/dist punto lejano
Corrijanme si me equivoco
d) Si la lente estuviera a 15 mm del ojo ¿Cual sería la potencia de la lente para leer cómodamente a 0.25 metros del ojo?
Aquí no se como tratar esos 15 mm.e) Un objeto de 100 mm de alto situado en su eje óptico, está a una distancia de 333 mm delante de la lente. ¿Cuál es la posición y tamaño de la imagen óptica dada por dicha lente?
Lo podría resolver por las fórmulas de aumentos?
Muchas gracias de antemano -
Un coche de 1200 kg se mueve a 72 km/h. En un instante apaga el motor y termina parándose en 75 m. Calcular la fuerza de rozamiento que ha permitido que se detenga
Antonio Silvio Palmitano
el 30/11/18Tienes los datos (observa que consideramos un sistema de referencia con eje de posiciones OX con dirección y sentido positivo acordes al desplazamiento del coche, con origen de coordenadas correspondiente a la posición del auto cuando su conductor apaga el motor):
M = 1200 Kg (masa del coche),
vi = 72 Km/h = 72*1000/3600 = 20 m/s (módulo de la velocidad inicial del coche),
vf = 0 (módulo de la velocidad final del coche),
xi = 0 (posición inicial del coche),
xf = 75 m (posición final del coche),
fr = a determinar (módulo de la fuerza de rozamiento).
Luego, observa que tienes dos opciones para plantear este problema:
a)
Con consideraciones de energía:
Planteas la expresión de la variación de energía cinética del coche, y queda:
ΔEC = ECf - ECi = (1/2)*M*(vf2 - vi2) = (1/2)*1200*(0 - 202) = -240000 J (1).
Planteas la expresión del trabajo de la fuerza de rozamiento (observa que su sentido es opuesto al sentido del desplazamiento del coche), y queda:
Wfr = -fr*(xf - xi) = -fr*(75 - 0) = -75*fr (2) (en Joules).
Planteas la ecuación trabajo-energía, y queda:
Wfr = ΔEC, sustituyes las expresiones señaladas (2) (1), y queda:
-75*fr = -240000, divides por -75 en ambos miembros, y queda:
fr = 3200 N.
b)
Con consideraciones cinemáticas y dinámicas:
Planteas la ecuación posición velocidad de Movimiento Rectilíneo Uniformemente Variado, y queda:
2*a*(xf - xi) = vf2 - vi2, reemplazas datos, y queda:
2*a*(75 - 0) = 02 - 202, resuelves operaciones numéricas, y queda:
150*a = -400, divides en ambos miembros por 150, y queda:
a = -8/3 m/s2, que es el valor de la aceleración del coche.
Aplicas la Segunda Ley de Newton (presta atención al sentido de la fuerza de rozamiento), y queda:
-fr = M*a, reemplazas valores, y queda:
-fr = 1200*(-8/3), resuelves el segundo miembro, multiplicas por -1 en ambos miembros, y queda:
fr = 3200 N.
Espero haberte ayudado.
-
Cuando cae un paracaídas abierto, ¿qué tipo de movimiento lleva?, ¿Qué fuerzas se ejercen sobre el paracaídas?, ¿Cómo son dichas fuerzas?
Gracias adelantadas
Javier Quintana
el 30/11/18Yo diría que las únicas fuerzas que hay son la del peso del propio paracaidista, la tensión en dirección hacia arriba de las cuerdas del paracaidas y la fuerza de rozamiento con el aire que también va hacia arriba. Y el tipo de movimiento supongo que un caída libre no? llegará un momento que peso y rozamiento se igualen y el cuerpo no será capaz de caer más rápido y empezará a descenser a velocidad constante
-
De qué formas puedo disimular un objetivo de una cámara con materiales de forma que quede tapado, pero que no me impida ver o grabar escenas ?
El caso de las pelis es un espejo que permite ver por el reverso y que por el derecho es un espejo.
Otros disimulos es utilizar un agujerito , pero realmente el objetivo no está tapado.
Qué más soluciones hay y cómo me hago con ellas ?
Gracias
-
Raúl RC
el 30/11/18Lucia, el profesor grabó unos videos sobre este tema excepcional que es propio de universidad (nivel que en unicoos no tocamos de momento). Te sugiero les eches un vistazo porque de seguro que te ayudarán enormemente.
Un saludo
Momento de inercia -
Hola unicoos.
Calcular la velocidad de escape desde la superficie de un asteroide esférico con 3km de radio y una densidad de 3g•cm-3
En la resolución,en concreto para hallar la masa del asteroide,aparece esto:
d=M/v=M/4/3πR3 =M=4/3πR3 d
Luego se resuelve así:
Ve=√2G4/3πR3 d/R=√8/3πG•d•R2 =√8/3π6,67•10-11 •3000•30002 =3,88m/s
Alguien que me explique los pasos de este proceso,por favor.
Gracias de antemano.
Raúl RC
el 28/11/18Lo que hacen es sustituir la masa del planeta (que no te la dan) de la expresion de al densidad d=m/V siendo el volumen el de una esfera aproximadamente que es 4/3πR3
quedando m=d·V=3·4/3·π·R3 pasando previamente la densidad a las unidades del SI. Finalmente sustituyes todo esto en la expresion de la velocidad de escape para llegar a la solucion final
Espero haberte aclarado
-
HOLA A TODOS. aLGUIEN ME PODRÍA AYUDAR CON ESTE PROBLEMA:
Un hombre camina en un bosque y está en un cierto momento a 5 km de un camino recto y a 13 km de una casa ubicada sobre el camino. El hombre puede caminar a 3 km/h en el bosque y a 5 km/h en el camino. Si camina en línea recta hasta el camino y después por el camino hasta la casa. ¿Cómo debe caminar para tardar un tiempo mínimo?
(Respuesta: x = 8,25km de la casa)Gracias!!!
Antonio Silvio Palmitano
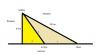
el 29/11/18Observa la figura, y en ella hemos designado:
con z a la distancia recorrida en el bosque,
con x a la distancia recorrida en el camino;
y observa que las dimensiones del triángulo rectángulo que es unión del triángulo amarillo con el triángulo marrón son:
altura: 5 Km (distancia del punto de salida al camino),
hipotenusa: 13 Km (distancia del punto de salida a la casa),
base: √(132-52) = √(169-25) = √(144) = 12 Km.
Luego, observa que las dimensiones del triángulo rectángulo amarillo son:
altura: 5 Km,
base: p (a determinar),
hipotenusa: z = (a determinar),
y puedes plantear la ecuación pitagórica:
z = √(52+p2) = √(25+p2) (1).
Luego, observa la unión de las bases de los dos triángulos sombreados, y puedes plantear:
p + x = 12, aquí restas p en ambos miembros, y queda:
x = 12 - p (2).
Luego, planteas la ecuación tiempo-desplazamiento de Movimiento Rectilíneo Uniforme para los dos trayectos que recorre el hombre, y quedan las ecuaciones:
vb*tb = z,
vc*tc = x;
luego, reemplazas los valores de las velocidades (vb = 3 Km/h, vc = 5 Km/h), y las expresiones señaladas (1) (2), y queda:
3*tb = √(25+p2),
5*tc = 12 - p;
luego, multiplicas por 1/3 en ambos miembros de la primera ecuación, multiplicas por 1/5 en ambos miembros de la segunda ecuación, y queda:
tb = (1/3)*√(25+p2) (3),
tc = (1/5)*(12 - p) (4).
Luego, planteas la expresión del intervalo de tiempo total (T), y queda:
T = tb + tc, sustituyes las expresiones señaladas (3) (4), y queda:
T = (1/3)*√(25+p2) + (1/5)*(12 - p) (5);
luego, derivas, y queda:
T ' = (1/3)*p/√(25+p2) - 1/5 (6);
luego, planteas la condición de punto estacionario (posible máximo o posible mínimo), y queda:
T ' = 0, sustituyes la expresión señalada (6), y queda:
(1/3)*p/√(25+p2) - 1/5 = 0, sumas 1/5 en ambos miembros, y queda:
(1/3)*p/√(25+p2) = 1/5, multiplicas por 15*√(25+p2) en ambos miembros, y queda:
5*p = 3*√(25+p2), elevas al cuadrado en ambos miembros (observa que resolvemos y simplificamos factores), y queda:
25*p2 = 9*(25 + p2), distribuyes el segundo miembro, y queda:
25*p2 = 225 + 9*p2, restas 9*p2 en ambos miembros, y queda:
16*p2 = 225, divides por 16 en ambos miembros, y queda:
p2 = 225/16, extraes raíz cuadrada en ambos miembros, y queda:
p = 15/4 Km = 3,75 Km;
luego reemplazas el valor remarcado en las ecuaciones señaladas (1) (2) (3) (4) (5), resuelves, y queda:
z = √(25+(15/4)2) = = √(25+225/16) = √(625/16) = 25/4 Km = 6,25 Km,
x = 12 - 15/4 = 33/4 Km = 8,25 Km,
tb = (1/3)*√(25+(15/4)2) = (1/3)*(25/4) = 25/12 h ≅ 2,083 h,
tc = (1/5)*(12 - 15/4) = (1/5)*(33/4) = 33/20 h = 1,65 h,
T = (1/3)*√(25+p2) + (1/5)*(12 - p) = 25/12 + 33/20 = 56/15 h ≅ 3,733 h.
Luego, puedes concluir que los trayectos son:
z = 6,25 Km en el bosque, que el hombre recorre en: tb = 2,083 h,
x = 8,25 Km en el camino, que el hombre recorre en: tc = 1,65 h;
y observa que el trayecto total (x+z) es: 14,50 Km, que el hombre recorre en: T ≅ 3,733 h.
Espero haberte ayudado.