-
Raúl RC
el 28/11/18Fraanciscko Barreda son muchos problemas los que nos pides resolver, recuerda que atendemos dudas concretas.
Para estos casos lo recomendable es que acudas a los mas de 700 vídeos que el profe ha grabado sobre muchas tematicas de fisica, quimica, matematicas, etc
En tu caso puedo ver que son ejercicios de muelles, planos inclinados.
Te dejo estos links, espero te ayuden.
Ley de Hooke Plano inclinado Diagrama del cuerpo libre 01 -
Raúl RC
el 28/11/18Para el ejercicio 2 te recomiendo estos vídeos:
Tiro Vertical - Caída librePara el tercero:
a) La velocidad angular es la misma para los dos caballitos, sin importar lo lejos que estén del centro. Si no fuera así, algunos caballitos adelantarían a otros dentro del tiovivo. Si la calculas del mismo modo que en ejercicios anteriores, verás que el resultado es de π radianes/segundo.
Para el ejercicio 1)
La moto lleva un MRUA: x=0,5·a·t2=t2
El coche lleva un MRU: x=x0+v·t => siendo v=15 m/s en el SI, con lo cual:
x=0+15·t=15t
Igualando ambas expresiones:
t2-15t=0. La única solución válida es t=15 s
b) la distancia de alcance es x=152=225 m
c) la moto lleva una velocidad cuando le alcanza de:
v=v0+at=2·15= 30m/s
-
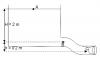
. El depósito de la figura contiene agua (H2O = 1 g/cm3
) hasta una altura H = 2 m,
tiene una sección SA = 1 m2 y está destapado (Patm = 1 atm). De la parte inferior
del depósito sale un tubo de sección constante S = 9 cm2 con un desnivel h = 0,2 m. Si a la salida del tubo hay un tapón que impide la salida del agua,a. Determinar las presiones en los puntos A, B y C.
b. Si ahora destapamos el tubo permitiendo la salida libre del agua. Determinar
las nuevas presiones en los puntos A, B y C.c. Si ahora destapamos el tubo permitiendo la salida libre del agua. ¿Cuál es
el caudal del agua que sale del depósito?ayuda por favor
Jerónimo
el 28/11/181atm=101300Pa
a)Antes de abrir el tapón
Pa=Patm=101300Pa
Pb=Patm+hbdg=101300+2x1000x10=121300 Pa
Pc=Patm+hcdg=101300+2,2x1000x10=123300 Pa
b)Abriendo el tapón
Pa=Pc=Patm=101300Pa
Aplicando Bernoulli a los puntos b y c. Pb+1/2ρvb ²+ρghb=Pc+1/2ρvc ²+ρghc Pc=Patm vb=vc y hc=0
Pb+1000x9,8x0,2=101300 Pb=99340 Pa
Aplicando Bernoulli a los puntos a y c Pa+1/2ρva ²+ρgha=Pc+1/2ρvc ²+ρghc Pa= Pc=Patm va=0 hc=0
gha=1/2vc ² 10x2,2=1/2vc² vc=6,63 m/s
Caudal Q=vA= 6,63m/s x 0,0009m²= 5,9x10^-3m³/s= 5,9 litros /s
-
alguien sabe como se hace:
Determine el camino x recorrido por un cuerpo durante el tiempo t, si su velocidad es proporcional al trayecto, sabiendo que en 10s el cuerpo recorre 100m y en 15s recorre 200m. (respuesta: x= 25.2Λ1/2t)
Antonio Silvio Palmitano
el 27/11/18Tienes la relación entre posición y velocidad:
v = k*x, expresas a la velocidad como la derivada de la posición con respecto al tiempo, y queda:
dx/dt = k*x, separas variables, y queda:
dx/x = k*dt, integras en ambos miembros, y queda:
lnx = k*t + c (*).
Luego, evalúas la ecuación implícita señalada (*) para la primera condición inicial (t = 10 s, x = 100 m), y queda:
ln(100) = k*10 + c, aquí restas k*10 en ambos miembros, y queda:
ln(100) - k*10 = c (1).
Luego, evalúas la ecuación implícita señalada (*) para la segunda condición inicial (t = 15 s, x = 200 m), y queda:
ln(200) = k*15 + c (2).
luego, sustituyes la expresión señalada (1) en la ecuación señalada (2), y queda:
ln(200) = k*15 + ln(100) - k*10, restas ln(100) en ambos miembros, reduces términos semejantes en el segundo miembro, y queda:
ln(200) - ln(100) = k*5, aplicas la propiedad del logaritmo de una división en el primer miembro, y queda:
ln(200/100) = k*5, resuelves el argumento del logaritmo, multiplicas por 1/5 en ambos miembros, y queda:
(1/5)*ln(2) = k;
luego, reemplazas el valor remarcado en la ecuación señalada (1), y queda:
ln(100) - (1/5)*ln(2)*10 = c, resuelves factores racionales en el segundo término, y queda:
ln(100) - 2*ln(2) = c, aplicas la propiedad del logaritmo de una potencia en el segundo término, y queda:
ln(100) - ln(22) = c, aplicas la propiedad del logaritmo de una división en el primer miembro, y queda:
ln(100/22) = c, resuelves el argumento del logaritmo, y queda:
ln(25) = c.
Luego, reemplazas los dos valores remarcados en la ecuación señalada (*), y queda:
lnx = (1/5)*ln(2)*t + ln(25), aplicas la propiedad del logaritmo de una potencia en el primer término del segundo miembro, y queda
lnx = ln(2(1/5)*t) + ln(25), aplicas la propiedad del logaritmo de una multiplicación en el segundo miembro, y queda:
lnx = ln(25*2(1/5)*t), compones en ambos miembros con la función inversa del logaritmo natural, y queda:
x = 25*2(1/5)*t,
que es la expresión de la posición del móvil en función del tiempo.
Espero haberte ayudado.
-
hola a todos. Alguien me puede ayudar con este problema:
Un cuerpo de 8 kg de peso cae partiendo del reposo desde una gran altura. Conforme cae, actúa sobre el la resistencia del aire a la que se supone numéricamente igual a 2v (en kg), siendo v la velocidad en m/s. Halle la velocidad y la distancia recorrida al cabo de t segundos.
graciasAntonio Silvio Palmitano
el 27/11/18Establece un sistema de referencia con eje de posiciones OY vertical, con sentido positivo hacia abajo, con origen de coordenadas en el punto de partida del móvil, y con instante inicial ti = 0.
Luego, observa que sobre el móvil actúan dos fuerzas verticales, de las que indicamos sus módulos y sentidos:
Peso: P = M*g = 8*10 = 80 N, hacia abajo (observa que su sentido es positivo),
Resistencia del aire: R = 2*v, hacia arriba (observa que su sentido es negativo);
luego, aplicas la Segunda Ley de Newton, y tienes la ecuación:
P - R = M*a, sustituyes expresiones, y queda:
80 - 2*v = 8*a, divides por 8 en todos los términos de la ecuación, y queda:
-0,25*v + 10 = a, restas a, restas 10 y sumas 0,25*v en ambos miembros, y queda:
-a = -10 + 0,25*v, multiplicas por -1 en todos los términos, y queda:
a = 10 - 0,25*v, expresas a la aceleración como la derivada de la velocidad con respecto al tiempo, y queda:
dv/dt = 10 - 0,25*v, separas variables, y queda:
dv/10-0,25*v) = dt, integras en ambos miembros, y queda:
-4*ln(10-0,25*v) = t + c (1),
reemplazas los valores de la condición inicial (t = 0, v = 0), cancelas términos nulos, y queda:
-4*ln(10) = c, reemplazas este valor en la ecuación señalada (1), y queda:
-4*ln(10-0,25*v) = t - 4*ln(10), sumas 4*ln(10) en ambos miembros, y queda:
-4*ln(10-0,25*v) + 4*ln(10) = t, multiplicas por -1/4 en todos los términos, y queda:
ln(10-0,25*v) - ln(10) = -(1/4)*t, aplicas la propiedad del logaritmo de una división en el primer miembro, y queda:
ln( (10-0,25*v)/10 ) = -(1/4)*t, compones en ambos miembros con la función inversa del logaritmo natural, y queda:
(10 - 0,25*v)/10 = e-(1/4)*t, multiplicas por 10 en ambos miembros, y queda:
10 - 0,25*v = 10*e-(1/4)*t, restas 10 en ambos miembros, y queda:
-0,25*v = -10 + 10*e-(1/4)*t, multiplicas por -4 en todos los términos, y queda:
v = 40 - 40*e-(1/4)*t,
que es la expresión de la velocidad en función del tiempo.
Luego, expresas a la velocidad como la derivada de la posición con respecto al tiempo, y queda:
dy/dt = 40 - 40*e-(1/4)*t, separas variables, y queda:
dy = (40 - 40*e-(1/4)*t)*dt, integras en ambos miembros, y queda:
y = 40*t + 40*e-(1/4)*t + d (2),
reemplazas los valores de la condición inicial (t = 0, y = 0, aquí recuerda que establecimos el origen de coordenadas en el punto de partida del móvil), cancelas términos nulos, y queda:
0 = 40 + d, restas 40 en ambos miembros, y queda:
-40 = d, reemplazas este valor en la ecuación señalada (2), y queda:
y = 40*t + 40*e-(1/4)*t - 40,
que es la expresión de la posición del móvil en función del tiempo.
Espero haberte ayudado.
-
Por una tubería de radio 25 cm circula agua a 12m/s bajo una presión de 2000 kPa. La tubería se estrecha hasta la mitad de su diámetro original. Hallar
a) la velocidad
b) la presión del agua en la parte más estrecha de la tubería
necesito ayuda con este ejercicio
Antonio Silvio Palmitano
el 27/11/18Tienes la densidad de masa del agua líquida:
δ = 1000 Kg/m3.
Tienes los datos de la sección transversal más amplia de la tubería, cuyo radio es R1 = 0,25 m:
A1 = π*R12 = π*0,252 = 0,0625π m2,
v1 = 12 m/s,
p1 = 2000000 Pa.
Tienes los datos de la sección transversal más estrecha de la tubería, cuyo radio es R2 = R1/2:
A2 = π*0,252/4 = 0,015625π m2,
v2 = a determinar,
p2 = a determinar.
Consideramos que el eje de simetría de la tubería es horizontal.
Luego, planteas la ecuación de continuidad, planteas la ecuación de Bernoulli, y queda:
A2*v2 = A1*v1,
p2 + (1/2)*δ*v22 = p1 + (1/2)*δ*v12;
sustituyes expresiones, y las ecuaciones quedan:
0,015625π*v2 = 0,0625π*12,
p2 + (1/2)*1000*v22 = 2000000 + (1/2)*1000*122;
divides por 0,015625π en ambos miembros de la primera ecuación, resuelves coeficientes en la segunda ecuación, y queda:
v2 = 4 m/s,
p2 + 500*v22 = 2000000 + 72000;
reemplazas el valor remarcado en la segunda ecuación, resuelves, y queda:
p2 + 8000 = 2072000,
restas 8000 en ambos miembros, y queda:
p2 = 2064000 Pa = 2064 KPa.
Espero haberte ayudado.
-
Desde la ventana de una casa se lanzan dos piedras en dirección vertical y con la misma velocidad inicial de 100 m/s en valor absoluto. Una de las piedras se lanza hacia arriba y la otra hacia abajo. ¿Con qué diferencia de tiempo llegan al suelo? Despréciese el rozamiento con el aire.
Hola únicos. He hecho este problema hallando el tiempo que la primera piedra tarda en alcanzar la altura máxima. Luego "por la cuenta de la vieja" la solución me da 20, 4 segundos. Mi profe me pide que se lo plasme con una fórmula, y no sé cómo hacerlo porque siempre me faltan datos con la piedra que va para abajo. ¿Alguna sugerencia?
Antonio Silvio Palmitano
el 27/11/18Establece un sistema de referencia con instante inicial: ti = 0, y con eje OY vertical con sentido positivo hacia arriba, con origen de coordenadas al nivel del suelo.
Luego, tienes los datos:
H = a determinar (posición de la ventana),
|vi| = 100 m/s (módulo de la velocidad inicial de las piedras),
a = -g = -10 m/s2 (aceleración de las piedras).
Luego, planteas la ecuación de posición para la piedra que inicialmente asciende, y queda:
y1 = H + |vi|*t - (1/2)*g*t2;
luego, planteas la condición de llegada al suelo: t1 = a determinar, y1 = 0, sustituyes, y queda:
0 = H + |vi|*t - (1/2)*g*t12, multiplicas en todos los términos por 2/g, y queda:
0 = 2H/g + 2*(|vi|/g)*t - t12, sumas t12 y restas 2*(|vi|/g)*t1 en ambos miembros, y queda:
t12 - 2*(|vi|/g)*t1 = 2H/g, sumas (|vi|/g)2 en ambos miembros, y queda:
t12 - 2*(|vi|/g)*t1 + (|vi|/g)2 = (|vi|/g)2 + 2H/g,
factorizas el trinomio cuadrado perfecto en el primer miembro, resuelves la potencia en el primer término y extraes denominador común en el segundo miembro, y queda:
(t1 - |vi|/g)2 = (|vi|2 + 2gH)/g2, extraes raíz cuadrada en ambos miembros (observa que elegimos la raíz positiva), y queda:
t1 - |vi|/g = +√(|vi|2 + 2gH)/g, sumas |vi|/g en ambos miembros, y queda:
t1 = |vi|/g + √(|vi|2 + 2gH)/g.
Luego, planteas la ecuación de posición para la piedra que desciende desde el inicio, y queda:
y2 = H - |vi|*t - (1/2)*g*t2;
luego, planteas la condición de llegada al suelo: t2 = a determinar, y2 = 0, sustituyes, y queda:
0 = H - |vi|*t2 - (1/2)*g*t22, multiplicas en todos los términos por 2/g, y queda:
0 = 2H/g - 2*(|vi|/g)*t2 - t22, sumas t22 y sumas 2*(|vi|/g)*t2 en ambos miembros, y queda:
t22 + 2*(|vi|/g)*t2 = 2H/g, sumas (|vi|/g)2 en ambos miembros, y queda:
t22 + 2*(|vi|/g)*t2 + (|vi|/g)2 = (|vi|/g)2 + 2H/g,
factorizas el trinomio cuadrado perfecto en el primer miembro, resuelves la potencia en el primer término y extraes denominador común en el segundo miembro, y queda:
(t2 + |vi|/g)2 = (|vi|2 + 2gH)/g2, extraes raíz cuadrada en ambos miembros (observa que elegimos la raíz positiva), y queda:
t2 + |vi|/g = +√(|vi|2 + 2gH)/g, restas |vi|/g en ambos miembros, y queda:
t2 = -|vi|/g + √(|vi|2 + 2gH)/g.
Luego, planteas la expresión del intervalo de tiempo determinado por los instantes de llegada al suelo de las piedras, y queda:
Δt = t1 - t2,
sustituyes las expresiones remarcadas, y queda:
Δt = |vi|/g + √(|vi|2 + 2gH)/g - (-|vi|/g + √(|vi|2 + 2gH)/g),
distribuyes el agrupamiento, y queda:
Δt = |vi|/g + √(|vi|2 + 2gH)/g) + |vi|/g - √(|vi|2 + 2gH)/g),
cancelas términos opuestos, y queda:
Δt = |vi|/g + |vi|/g ,
reduces términos semejantes, y queda:
Δt = 2*|vi|/g,
que es la expresión del intervalo de tiempo en función del módulo de las velocidades iniciales de las piedras y del módulo de la aceleración gravitatoria terrestre;
luego, tienes para este problema:
Δt = 2*100/10 = 20 s.
Espero haberte ayudado.
-
Hola unicoos, podeis ayudarme con este problema?
Disponemos de una carga puntual de -5mC en el origen de coordenadas. A una distancia de 20 cm de esta hay una carga de 3 nC en reposo. Le aplicamos una fuerza radial hacia fuera de 4N ¿Que energia cinetica tendra cuando se encuentre a una distancia de 1 m ?
Espero vuestro resultado, muchas gracias besitos !!
Antonio Silvio Palmitano
el 26/11/18Tienes los valores de la carga fija y de la carga móvil, y sus posiciones:
qA = - 5mC = -5*10-3 C,
cuya posición es: rA = 0;
qB = +3nC = 3*10-9 C,
cuya posición inicial es: rBi = 20 cm = 0,2 m, y cuya posición final es: rBf = 1 m.
Tienes el valor de la fuerza aplicada sobre la carga móvil:
F = +4 N.
Luego, observa que sobre la carga móvil actúan dos fuerzas, de las que indicamos sus módulos y sentidos:
Fuerza de atracción electrostática:
Fe = k*|qA|*qB/(rBf-rBi)2 = 9*109*5*10-3*3*10-9/0,82 = 2,109375*10-1 N, hacia la carga fija;
Fuerza externa:
F = 4 N, alejándose de la carga fija;
luego, planteas la expresión de la Fuerza Resultante, y queda:
FR = F - Fe = 4 - 2,109375*10-1 = 3,7890625 N, alejándose de la carga fija.
Luego, planteas la expresión del trabajo de la fuerza resultante (observa que la fuerza y el desplazamiento tienen el mismo sentido), y queda:
WR = FR*(rBf-rBi) = 3,7890625*(1-0,2) = 3,03125 J,
que queda asociado a la partícula móvil como energía cinética.
Espero haberte ayudado.
-
Buenas noches.
Pueden ayudarme con este problema porfavor:
Se sube un cuerpo que normalmente esta en reposo y que pesa 2.5 kg a lo largo de un plano inclinado que forma un ángulo de 31 grados con la horizontal, aplicando una fuerza F paralela al plano de magnitud 14.5 kilos.
El coeficiente de fricción entre el cuerpo y el plano es 0.12.
1-Calcula el trabajo realizado por F para que el cuerpo suba una distancia de 13 metros 2-¿Que parte de ese trabajo se va en vencer la fuerza de fricción?3- Al llegar al final de su recorrido se suelta el cuerpo. Obtenga usando argumentos energéticos, la velocidad con que llega al suelo.Raúl RC
el 26/11/18Te recomiendo encarecidamente que veas este vídeo que grabó el profe sobre esta temática, en él explica toda la teoria que necesitas.
Es un problema bastante largo por aqui y sería interesante que hubieras aportado algo mas que el enunciado.
Espero te sirva, nos cuentas ;)
https://www.youtube.com/watch?v=50GUrSoGUIk