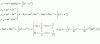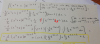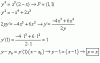-
buenas a ver quien puede ayudarme para resolver este ejercicio, y sobre todo una pequeña explicación como hacer el ejercicio que seguro que me ponen mas de estos
Jose Ramos
el 3/12/19Joaquin Gonzalez Torres
el 3/12/19 -
-
Antonio Silvio Palmitano
el 3/12/19Observa que puedes plantear la ecuación diferencial:
dV/dt = k*S (*),
donde k es una constante de proporcionalidad (observa que debe ser negativa).
Luego, tienes la expresión del volumen en función del radio (observa que extraemos el valor del radio a partir del valor del diámetro que tienes en tu enunciado, y que expresamos a los radios en centímetros y, más adelante, a los tiempos en minutos):
v = (4π/3)*R3, de donde tienes:
dV/dt = (4π/3)*3*R2*dR/dt = 4π*R2*dR/dt (1).
Luego, tienes la expresión del área de la bola en función de su radio:
S = 4π*R2 (2).
Luego, sustituyes las expresiones señalada (1) (2) en la ecuación diferencial señalada (*), y queda:
4π*R2*dR/dt = k*4π*R2, divides por 4π*R2 en ambos miembros, y queda:
dR/dt = k, separas variables, y queda:
dR = k*dt, integras en ambos miembros, y queda:
R = k*t + C (3),
que es la expresión general del radio de la bola en función del tiempo;
reemplazas los valores iniciales: t = 0 y R = 2 cm en la ecuación señalada (3), y queda: C = 2,
reemplazas este valor remarcado en la ecuación señalada (3), y queda:
R = k*t + 2 (4).
Luego, tienes los datos en estudio: t = 30 min y R = 1,5 cm,
reemplazas estos valores en la ecuación señalada (4), y queda:
1,5 = k*30 + 2, y de aquí despejas: k = -1/60,
reemplazas este valor remarcado en la ecuación señalada (4), y queda:
R = -(1/60)*t + 2 (5),
que es la expresión del radio de la bola en función del tiempo para las condiciones planteadas en tu enunciado.
Luego, tienes la última condición en estudio: R = 1 cm,
reemplazas este valor en la ecuación señalada (5), y queda:
1 = -(1/60)*t + 2, y de aquí despejas: t = 60 min.
Espero haberte ayudado.
-
Me gustaría tener ayuda con el siguiente problema con el uso de integrales definidas:
Un ciclista pesa 80 kg al iniciar una etapa a contrarreloj de 200 km. A lo largo de la carrera pierde peso a un ritmo de f(x) = 10^-6 * x^2 kg/km donde x = kilómetros.
1. Hallar función peso del ciclista a lo largo de la carrera.
2. Peso al finalizar la carrera.
3. ¿Cuanto peso pierde entre los kilómetros 100 y 150?
4. Ritmo medio de pérdida de peso en los últimos 100 km
5. Si el ciclista debe tomar algo cuando ha perdido el 2% de su peso, en kilómetro se para a tomar algo
-
César
el 3/12/19Jose Ramos
el 3/12/19 -
-
Antonio
el 3/12/19César
el 3/12/19