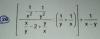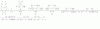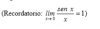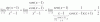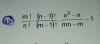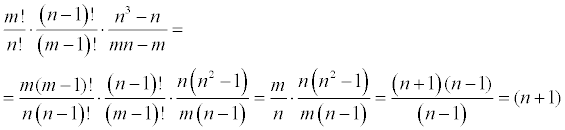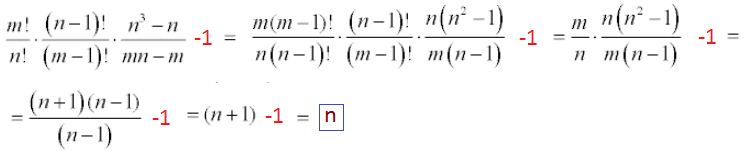Los foros de unicoos se han unificado en beUnicoos. Para dejar preguntas nuevas deberás hacerlo allí, donde además encontrarás el resto de asignaturas y herramientas para ayudarte con tus estudios.
Ir a beUnicoos
¿Cómo los resuelvo?
Hola, como se haría el siguiente límite:
Al hacerlo por L´Hopital me da 2, pero el ejercicio me pide que use: 
¿Cómo se haría usando esto? Gracias de antemano.
saludos
https://www.youtube.com/watch?v=Lg9fOAgpkOw y toda su lista de reproducción para continuidad.
https://www.youtube.com/watch?v=icZDdqfHAUo y toda su lista de reproducción para limites.
https://www.youtube.com/watch?v=yoAPeT7_mq8 y toda su lista de reproducción para asintotas.
Hay muchos ejercicios de limites. Con que pongas el Internet "limites" unicoos o el temario que quieras unicoos te va a salir. También puedes buscar por aquí https://www.unicoos.com/asignatura/matematicas según tu curso, pero a veces puedes ir mas adelantado de curso, piden mas nivel y demás
Ayuda por favor con la número 5 el inciso g
multiplica p * q e integra
Halla los componentes de los vectores ortonormales a u = (2,1)
Comienza por plantear la expresión de un vector genérico: p = < x , y >.
Luego, plantea la condición de perpendicularidad entre el vector u y el vector p (el producto escalar entre ellos debe ser igual a cero):
< 2 , 1 > • < x , y > = 0, desarrollas el producto escalar y queda la ecuación:
2x + y = 0, haces pasaje de término, y queda:
y = -2x;
luego, sustituyes en la expresión del vector genérico, y queda:
p = < x , -2x >, extraes el factor escalar (x), y queda:
p = x*< 1 , -2 >;
por lo que tienes que los vectores normales al vector u son múltiplos escalares del vector:
P = < 1 , -2 > (1).
Luego, planteas la expresión del módulo del vector P, y queda:
|P| = √( 12 + (-2)2 ) = √(5).
Luego, plantea las expresiones de los vectores unitarios paralelos al vector P:
P1 = P / |P| = < 1 , -2 > / √(5) = < 1/√(5) , -2/√(5) >;
P2 = -P / |P| = < -1 , 2 > / √(5) = < -1/√(5) , 2/√(5) >,
que son las expresiones de los dos vectores normales y unitarios (ortonormales) al vector u.
Espero haberte ayudado.
Hola! no puedo saca el siguiente limite (sin aplicar l'hospital)
limx-->0 (cos(6x)-cos(2x))/x^2
Gracias!
Recuerda la identidad trigonométrica de transformación en producto de la resta de dos cosenos:
cos(a) - cos(b) = -2*sen( (a+b)/2 )*sen( (a-b)/2 );
y observa que en tu enunciado corresponde asignar: a = 6x, b = 2x;
luego, sustituyes expresiones, resuelves argumentos, y queda:
cos(6x) - cos(2x) = -2*sen(4x)*sen(2x) (1).
Luego, tienes el argumento del límite de tu enunciado:
f(x) = ( cos(6x) - cos(2x) ) / x2 = sustituyes = -2*sen(4x)*sen(2x) /x2;
luego, expresas al argumento como un producto de expresiones fraccionarias, y queda:
f(x) = -2*( sen(4x) / x )*( sen(2x) / x );
luego, multiplicas y divides por 4 en el primer agrupamiento, multiplicas y divides por 2 en el segundo agrupamiento, extraes los factores de los numeradores, y queda:
f(x) = -2*4*2*( sen(4x) / 4x )*( sen(2x) / 2x) = -16*( sen(4x) / 4x )*( sen(2x) / 2x ).
Luego, plantea el límite de tu enunciado:
L = Lím(x→0) ( cos(6x) - cos(4x) )/x2, sustituyes la expresión remarcada en el argumento del límite, y queda:
L = Lím(x→0) -16*( sen(4x) / 4x )*( sen(2x) / 2x), extraes el factor constante, expresas al límite como un producto de límites, y queda:
L = -16 * Lím(x→0) ( sen(4x) / 4x ) * Lím(x→0) ( sen(2x) / 2x );
aplicas las sustituciones (cambios de variables):
u = 4x (observa que u tiende a 0 cuando x tiende a cero) en el primer límite,
w = 2x (observa que w tiende a 0 cuando x tiende a cero) en el segundo límite;
luego, sustituyes expresiones, y queda:
L = -16 * Lím(u→0) ( sen(u) / u ) * Lím(w→0) ( sen(w) / w );
resuelves los límites (observa que son iguales a uno, como has visto en clase), y queda:
L = -16*1*1 = -16.
Espero haberte ayudado.
Buenas!!
Tengo dudas con este tipo de limites. Alguien me puede ayudar a aprender como se resuelven??
Gracias
Necesito el determinante de esto.
de resultado me da: -y^3+y^2+3y-3
Me da distinto
el -1 no es un -3
¿Cómo resuelvo el ejercicio?
Está correctamente resuelto por César, sólo que falta el "1" :
Alguien podría pasarme el enlace al algún vídeo de youtube que me expliquen el método de "Gauss". Gracias.
