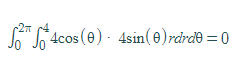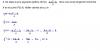-
Antonio Silvio Palmitano
el 29/11/19a)
Planteas la condición que cumplen los elementos pertenecientes al núcleo de la transformación lineal, y queda la ecuación vectorial:
T(x,y,z) = < 0 , 0 , 0 >, sustituyes la expresión de la transformación en el primer miembro, y queda:
< kx+3y , x-2y+z , kx+y-z > = < 0 , 0 , 0 >;
luego, por igualdad entre expresiones vectoriales, igualas componente a componente, y queda el sistema de ecuaciones:
kx + 3y = 0,
x - 2y + z = 0, de aquí despejas: z = -x + 2y (1),
kx + y - z = 0;
luego, mantienes la primera ecuación, sustituyes la expresión señalada (1) y reduces términos semejantes en la tercera ecuación, y queda;
kx + 3y = 0,
(k+1)x - y = 0, de aquí despejas: y = (k+1)x (2);
luego, sustituyes la expresión señalada (2) en la primera ecuación, y queda:
kx + 3(k+1)x = 0, distribuyes el segundo término, reduces términos semejantes, extraes factor común, y queda:
(4k+3)x = 0,
y observa que para que el sistema admita infinitas soluciones (que se corresponden con los infinitos puntos de la recta que es la representación gráfica del núcleo de la transformación), tienes que debe cumplirse la condición:
4k + 3 = 0, y de aquí despejas: k = -3/4 (3);
luego, reemplazas el valor señalado (3) en la expresión de la transformación lineal, y queda:
T(x,y,z) = < -(3/4)x+3y , x-2y+z , -(3/4)x+y-z >;
luego, reemplazas el valor señalado (3) en la ecuación señalada (2), resuelves, y queda: y = (1/4)x (4);
luego, sustituyes la expresión señalada (4) en la ecuación señalada (1), resuelves, y queda: z = -(1/2)x (5);
luego, planteas la expresión el vector genérico perteneciente al núcleo de la transformación lineal, y queda:
u = < x , y , z >;
luego, sustituyes las expresiones señalada (4) (5) en la expresión de este vector, y quea:
u = < x , (1/4)x , -(1/2)x >, extraes el factor común escalar, y queda:
u = x*< 1 , 1/4 , -1/2 >, por lo que tienes que el núcleo de la transformación queda expresado:
N(T) = { x*< 1 , 1/4 , -1/2 >, con x ∈ R },
y observa que su gráfica es una recta, que pasa por el origen de coordenadas, y uno de sus vectores directores es:
< 1 , 1/4 , -1/2 >,
por lo que las ecuaciones cartesianas paramétricas de la recta quedan:
x = t,
y = (1/4)*t,
z = -(1/2)*t,
con t ∈ R.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 29/11/19b)
Reemplazas el valor indicado (k = 1) en la expresión de la transformación lineal, y queda:
T(x,y,z) = < x+3y , x-2y+z , x+y-z >,
por lo que tienes que la expresión general de un vector que es elemento de la imagen de la transformación lineal es:
w = < x+3y , x-2y+z , x+y-z >,
expresas al segundo miembro como una suma de tres vectores, cada uno de ellos asociado a una de las indeterminadas, y queda:
w = < x , x , x > + < 3y , -2y , y > + < 0 , z , -z >,
extraes los factores escalares en todos los términos, y queda:
w = x*< 1 , 1 , 1 > + y*< 3 , -2 , 1 > + z*< 0 , 1 , -1 >,
por lo que tienes que una posible base de la imagen de la transformación lineal es el conjunto:
A = { < 1 , 1 , 1 > , < 3 , -2 , 1 > , < 0 , 1 , -1 > },
y solamente queda que demuestres que los tres vectores de este conjunto son linealmente independientes (te dejo la tarea), y en caso que no lo sean, deberás descartar el vector que sea combinación lineal de los demás.
En este caso, tienes que los tres vectores son linealmente independientes, por lo que puedes concluir que el conjunto A es una base de la imagen, y como su cardinal es |A| = 3, entonces tienes que la dimensión de la imagen es 3 y, por lo tanto, tienes que la imagen de la transformación lineal es el espacio vectorial R3.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 29/11/19Observa que la integral doble que has propuesto corresponde a una región de integración que es un disco completo, con centro en el origen de coordenadas y radio cuatro, pero observa que la región de integración es la mitad "derecha" de dicho disco (observa que la variable x toma valores positivos comprendidos entre cero y cuatro), por lo que tienes un cuarto de disco en el cuarto cuadrante y otro cuarto de disco en el primer cuadrante;
luego, tienes que con el paso a coordenadas polares (no olvides el factor de compensación Jacobiano: |J| = r) queda:
I = -π/2∫π/20∫4 (r*cosθ)*(r*senθ)*r*dr*dθ = -π/2∫π/20∫4 (r3*senθ*cosθ)*dr*dθ = -π/2∫π/20∫4 ( r3*(1/2)sen(2*θ) )*dr*dθ,
extraes el factor constante, integras para la primera variable (r, y observa que indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:
I = (1/2)*-π/2∫π/2 sen(2*θ)*[ r4/4 ]*dθ = (1/2)*-π/2∫π/2 sen(2*θ)*[ 64 ]*dθ = 32*-π/2∫π/2 sen(2*θ)*dθ,
integras para la segunda variable (θ, y observa que indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:
I = 32*[ -(1/2)*cos(2*θ) ] = 32*[ -(1/2)*cos(π) - ( -(1/2)*cos(-π) ) ] = 32*[ 1/2 - 1/2 ] = 32*0 = 0.
Espero haberte ayudado.
-
Breaking Vlad
el 29/11/19Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis siempre también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro.
-
Combinatoria: Con las cifras impares formo números de 4 cifras. Si los ordenamos de pequeño a grande, qué lugar ocupa el número 7319?
Jose Ramos
el 28/11/19Suponiendo que las cifras no se pueden repetir. Entonces:
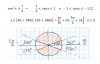
Comienzan por 1 Variaciones de 4 tomadas de 3 en 3 V4,3 = 24 Analogamente comienzan por 3, 24 y por 5, 24.
Fijo el 7 en primera posición comienzan por 71 V 3,2 = 6
Tenemos a continuación 7315, 7319. Entonces el número 7319 ocupa el lugar 24.3 + 6 + 2 = 80
Jose Ramos
el 28/11/19Suponiendo que las cifras se pueden repetir. Entonces:
Comienzan por 1 Variaciones con repetición de 5 tomadas de 3 en 3 VR5,3 = 53 =125. Analogamente comienzan por 3, 125 y por 5, 125.
Fijo el 7 en primera posición comienzan por 71 VR 5,2 = 25
Tenemos a continuación 7311, 7313, 7315, 7317, 7319 Entonces el número 7319 ocupa el lugar 125.3 + 25 + 5 = 405