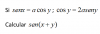-
En mi pregunta anterior me has dado la siguiente respuesta
Había llegado a los mismos resultados de la parábola y la recta, entiendo que hay que montar una función don las dos funciones.
Me podrías explicar el por que de los < y >= en la función final, no termino de entender por que de cada uno.
Muchas gracias
-
Antonio Silvio Palmitano
el 11/11/19Vamos con una orientación
Tienes las ecuaciones trigonométricas
senx = a*cosy (1),
cosy = 2a*seny (2).
Luego, divides por 2a y por cosy en ambos miembros de la ecuación señalada (2), y queda:
1/(2a) = seny/cosy, aplicas la identidad trigonométrica de la tangente en el segundo miembro, y luego despejas
tany = 1/(2a) (3).
Luego, planteas la identidad trigonométrica del coseno en función de la tangente para la incógnita y, y queda:
cos2y = 1/(1 + tan2y), sustituyes la expresión señalada (3) en el denominador, lo resuelves, y queda:
cos2y = 1/[1 + 1/(4a2)], extraes denominador común en el denominador de esta expresión, y queda:
cos2y = 1/[(4a2 + 1)/(4a2)], resuelves la división entre expresiones, y queda:
cos2y = 4a2/(4a2 + 1), extraes raíz cuadrada (consideramos la opción positiva), y queda:
cosy = 2a/√(4a2 + 1) (4);
luego, planteas la identidad trigonométrica del seno en función de la tangente para la incógnita y, y queda:
sen2y = tan2y/(1 + tan2y), sustituyes la expresión señalada (3) en el segundo miembro, lo resuelves, y queda:
sen2y = [1/(4a2)]/(1 + 1/(4a2), extraes denominador común en el denominador del segundo miembro, y queda:
sen2y = [1/(4a2)]/[(4a2 + 1)/(4a2)], resuelves la división de expresiones en el segundo miembro, y queda:
sen2y = 1/(4a2 + 1), extraes raíz cuadrada (consideramos la opción positiva), y queda:
seny = 1/√(4a2 + 1) (5).
Luego, sustituyes la expresión señalada (4) en la ecuación señalada (1), resuelves su segundo miembro, y queda:
senx = 2a2/√(4a2 + 1) (6);
luego, planteas la identidad trigonométrica del coseno en función del seno para la incógnita x, y queda:
cos2x = 1 - sen2x, sustituyes la expresión señalada (6) en el último término, lo resuelves, y queda:
cos2x = 1 - 4a4/(4a2 + 1), extraes denominador común en el segundo miembro, y queda:
cos2x = (4a2 + 1 - 4a4)/(4a2 + 1), extraes raíz cuadrada positiva en ambos miembros, y queda:
cosx = √[(4a2 + 1 - 4a4)/(4a2 + 1)], distribuyes la raíz cuadrada, y queda:
cosx = √(4a2 + 1 - 4a4)/√(4a2 + 1) (7).
Luego, planteas la expresión del seno de la suma que indican en tu enunciado, y queda:
sen(x + y) = senx*cosy + cosx*seny,
sustituyes las expresiones remarcadas y señaladas (6) (4) (7) (5), y queda:
sen(x + y) = [2a2/√(4a2 + 1)]*[2a/√(4a2 + 1)] + [√(4a2 + 1 - 4a4)/√(4a2 + 1)]*[1/√(4a2 + 1)],
resuelves las multiplicaciones de expresiones en ambos términos del segundo miembro, y queda:
sen(x + y) = 4a3/(4a2 + 1) + √(4a2 + 1 - 4a4)/(4a2 + 1),
extraes denominador común en el segundo miembro, y queda:
sen(x + y) = [4a3 + √(4a2 + 1 - 4a4)]/(4a2 + 1).
Espero haberte ayudado.
-
pq en un intervalo abierto una funcion es derivable en todo su dom pero en el cerrado en todo su dom menos en sus extremos?
Jose Ramos
el 10/11/19Si el dominio de la función f es un intervalo cerrado [a,b] y es derivable en el abierto (a,b) , en los extremos no se considera derivable porque no existe la derivada por la izquierda en a, ni la derivada por la derecha en b. Para que la función sea derivable en un punto, las derivadas laterales deben coincidir. Si quisiéramos calcular por ejemplo la derivada por la izquda en a, sería lim (h -> 0-) f(a+h)-f(a) / h, pero si h -> 0- h <0 y a+h < a, con lo cual a+h no está en el dominio [a,b] y por tanto f(a+h) no existe.
-
-
Jose Ramos
el 10/11/19Joaquin Gonzalez Torres
el 11/11/19