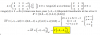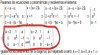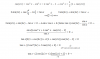-
Sara
el 16/3/17Hola, la última parte de este ejercicio no llego a entenderlo:
¿Forman los vectores {(2,0,-1), (1,2,1), (3,0,0), (-2,-1,1)} una base de ℝ3? Razona la respuesta. En cualquier caso, construye una base B’ de ℝ3 con al menos dos de los vectores dados y halla las coordenadas del punto P (-1,-4-0) respecto de B’.
-
valeria
el 16/3/17Hola,
Alguien me puede ayudar con el apartado B) del ejercicio 25
Sean los planos
a) 2x+3y+z+2=0
b) x+y-z=1
Obten la ecuación de una recta r que sea paralela a la intersección de a) y b) y que pase por el punto P(5,-3,1)
Gracias
-
Teresa Brocal Peña
el 16/3/17 -
Miquel Marcelo
el 16/3/17 -
ana
el 16/3/17 -
Sara
el 16/3/17Hola, ¿alguien puede ayudarme a calcular el área entre una recta y una parábola usando la integral?
Aplica la integral al cálculo del área encerrada entre la recta f(x)= 2x+2 y la parábola g(x)=3x2-4x+2 que queda por debajo de la recta, entre los valores x=0 y x=2.
Antonio Silvio Palmitano
el 16/3/17Observa que para x = 0 tienes y = 2, tanto para la recta como para la parábola, y que par ax = 2 tienes y = 6, también para ambas curvas. Luego, observa que para un valor intermedio, por ejemplo x = 1, tienes y = 4 en la recta, y tienes y = 2 para la parábola, por lo que si observas la gráfica, verás que la región limitada por ambas curvas está limitada superiormente por la recta, e inferiormente por la parábola, por lo tanto planteamos para el área (observa que el intervalo para x es: 0 ≤ x ≤ 2):
A = ∫ ( f(x) - g(x) )dx = ∫ ( 2x + 2 - (3x2 - 4x + 2) )dx = ∫ (2x + 2 - 3x2 + 4x - 2) dx =
= ∫ (- 3x2 + 6x)dx = integramos (indicamos con corchetes que debemos evaluar con la Regla de Barrow):
= [ - x3 + 3x2 ] = evaluamos = (- 8 + 12) - (- 0 + 0) = 4.
Espero haberte ayudado.
-
Andres Valenzuela
el 16/3/17 -
Sandy Murillo S...
el 16/3/17Hola amigos de unicoos, saludos. Os pido como petición que me colaboren en la resolución del problema planteado, no sé como desaparecer √3
¿Cómo se procede?
______________________ & Muchisisismas gracias le doy a la persona que brinde su ayuda. La necesito
-
Toby
el 16/3/17 -
Deidara Stick.
el 16/3/17Hola - Algún unicoo podría ayudarme con el siguiente ejercicio. Gracias de antemano
