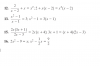-
Hola, alguien sabe como resolver este ejercicio?, Si un pozo bombea agua en un taza de 30 L/min ¿cuantas horas se llena el tanque con un volumen de 286.2783 m^3?
-
 Hola Cesar. Una factorización que no comprendo.
Hola Cesar. Una factorización que no comprendo.Incluyo imagen de la factorización con la ‘x’ que no entiendo. Gracias de antemano.

César
el 8/8/19√cuando factorizampos polimomios del tipo x^3+2x^2-6x=0 podemos sacr factor común x x(x^2+2x-6)=0
una de las soluciones es x=0 ya que verifica la ecuación
la otra solución vendrá al resolver (x^2+2x-6)=0 por el mismo motivo así pues la factorización quedará como sigue
x(x-a)(x-b)=0 con a =-1-√7 y b=-1+√7
Factorizacion de polinomios 01

Antonio Silvio Palmitano
el 8/8/19Tienes la expresión del polinomio:
P(x) = 2x4 - 6x3 - 6x2, extraes factores comunes (2x2), y queda:
P(x) = 2x2*(x2 - 3x - 3) (1).
Luego, aplicas la fórmula resolvente para determinar las sraíces del polinomio cuadrático que tienes en el agrupamiento, y tienes que estas raíces son:
x1 = 3/2 - √(21)/2, y x2 = 3/2 + √(21)/2;
luego, sustituyes la expresión factorizada del agrupamiento de la expresión del polinomio señalada (1), y queda:
P(x) = 2x2*( x - (3/2 - √(21)/2) )*( x - (3/2 + √(21)/2) ), distribuyes los segundos términos en los agrupamientos, y queda:
P(x) = 2x2*( x - 3/2 + √(21)/2 )*( x - 3/2 - √(21)/2 ),
que es la expresión factorizada del polinomio que tienes en tu enunciado,
y observa que las raíces de los factores son:
a = 0, con multiplicidad 2, para el factor: x2, que también puede expresarse: (x - 0)2,
b = 3/2 - √(21)/2, con multiplicidad 1, para el factor: ( x - 3/2 + √(21)/2 ),
c = 3/2 + √(21)/2, con multiplicidad 1, para el factor: ( x - 3/2 - √(21)/2 ),
y deberás consultar con tus docentes por la omisión del coeficiente principal (2) en la expresión factorizada del polinomio que tienes consignada en tu imagen. en la que se muestra la expresión factorizada del polinomio mónico asociado al polinomio P.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 7/8/19Puedes comenzar por escribir a todos los números, y a los que estén expresados en forma decimal (observa que indicamos en negrita a las cifras decimales periódicas, y revisa tus apuntes de clase si es necesarios para expresarlas en forma fraccionaria) los expresas también en forma fraccionaria, y queda:
3/7,
0'4 = 4/10 = 2/5,
1/5,
-0,9 = -(9 - 0)/9 = -9/9 = -1,
-1/3,
2/5,
0'01 = (1 - 0)/90 = 1/90,
0'73 = (73 - 7)/90 = 66/90 = 11/15.
Luego, expresas a todos con el mínimo común denominador, observa que en este caso es 630, y queda:
3/7 = 270/630,
0'4 = 2/5 = 252/630,
1/5 = 126/630,
-0,9 = -1 = -630/630,
-1/3 = -210/630,
2/5 = 252/630,
0,01 = 1/90 = 7/630,
0,73 = 11/15 = 462/630.
Luego, solo queda que ordenes las expresiones fraccionarias de mayor a menor, siguiendo a sus numeradores (te dejo la tarea).
Espero haberte ayudado.
-
Buenos dias, Necesito que ayuda con los siguientes ejercicios y agradeceria mucho contar con su ayuda. Muchas gracias de antemano
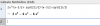
Las instrucciones son: En los problemas 7 a 16, determine qué operaciones se aplicaron a la primera ecuación para obtener la segunda. Establezca si las operaciones garantizan o no que las ecuaciones sean equivalentes. No resuelva las ecuaciones.


Antonio Silvio Palmitano
el 7/8/1912)
Tienes la ecuación:
2/(x-2) + x = x2, observa que x no puede ser igual a 2,
multiplicas por (x-2) en todos los términos de esta ecuación, simplificas, y queda:
2 + x(x-2) = x2(x-2), distribuyes los dos últimos términos, y queda:
2 + x2 - 2x = x3 - 2x2, restas x3 y sumas 2x2 en ambos miembros, reduces términos semejantes, ordenas términos, y queda:
-x3 + 3x2 - 2x + 2 = 0, multiplicas en todos los términos por -1, y queda:
x3 - 3x2 + 2x - 2 = 0,
que es una ecuación polinómica de tercer grado que no tiene raíces racionales, por lo que deberás consultar con tus docentes acerca de este ejercicio.
13)
Tienes la ecuación:
(x2 - 1)/(x - 1) = 3, observa que x no puede ser igual a 1,
factorizas el numerador en el primer miembro (observa que es una resta de cuadrados perfectos), y queda:
(x + 1)(x - 1)/(x - 1) = 3, simplificas en el primer miembro, y queda:
x + 1 = 3, restas 1 en ambos miembros, y queda:
x = 2.
15)
Tienes la ecuación:
2x(3x + 1)/(2x - 3) = 2x(x + 4), observa que x no puede ser igual a 3/2,
multiplicas por (2x - 3) en ambos miembros, y queda:
2x(3x + 1) = 2x(x + 4)(2x - 3), restas 2x(x + 4)(2x - 3) en ambos miembros, y queda:
2x(3x + 1) - 2x(x + 4)(2x - 3) = 0, extraes factores comunes, y queda:
2x( 3x + 1 - (x + 4)(2x - 3) ) = 0;
luego, por anulación de una multiplicación, tienes dos opciones:
1°)
2x = 0, divides por 2 en ambos miembros, y queda:
x = 0,
que puedes verificar que es una solución válida para la ecuación de tu enunciado, por lo que deberás consultar con tus docentes con respecto a ella;
2°)
3x + 1 - (x + 4)(2x - 3) = 0, distribuyes el tercer término, y queda:
3x + 1 - (2x2 - 3x + 8x - 12) = 0, reduces términos semejantes en el agrupamiento, y queda:
3x + 1 - (2x2 + 5x - 12) = 0, distribuyes el signo en el tercer término, y queda:
3x + 1 - 2x2 - 5x + 12 = 0, reduces términos semejantes, ordenas términos, y queda:
-2x2 - 2x + 13 = 0, multiplicas por -1 en todos los términos, y queda:
2x2 + 2x - 13 = 0, divides por 2 en todos los términos, y queda:
x2 + x - 13/2 = 0, sumas 13/2 en ambos miembros, y queda:
x2 + x = 13/2, sumas 1/4 en ambos miembros, y queda:
x2 + x + 1/4 = 27/4, factorizas el trinomio cuadrado perfecto en el primer miembro, y queda:
(x + 1/2)2 = 27/4, extraes raíz cuadrada en ambos miembros, y queda:
x + 1/2 = ±√(27/4), distribuyes la raíz y extraes factores fuera de la raíz cuadrada, y queda:
x + 1/2 = ±3√(3)/2, restas 1/2 en ambos miembros, y queda:
x = -1/2 ± 3√(3)/2, extraes denominador común, y queda:
x = ( -1 ± 3√(3) )/2, por lo que tienes dos opciones:
a)
x = ( -1 - 3√(3) )/2 ≅ -3,098;
b)
x = ( -1 + 3√(3 )/2 ≅ 2,098.
16)
Tienes la ecuación:
2x2 - 9 = x, restas x en ambos miembros, ordenas términos en el primer miembro, y queda:
2x2 - x - 9 = 0, multiplicas por 1/2 en todos los términos, y queda:
x2 - (1/2)x - 9/2 = 0, sumas 9/2 en ambos miembros, y queda:
x2 - (1/2)x = 9/2, sumas 1/16 en ambos miembros, y queda:
x2 - (1/2)x + 1/16 = 73/16, factorizas el trinomio cuadrado perfecto en el primer miembro, y queda:
(x - 1/4)2 = 73/16, extraes raíz cuadrada en ambos miembros, y queda:
x - 1/4 = ±√(73/16), distribuyes la raíz cuadrada, resuelves el denominador en el segundo miembro, y queda:
x - 1/4 = ±√(73)/4, sumas 1/4 en ambos miembros, y queda:
x = 1/4 ± √(73)/4, extraes denominador común, y queda:
x = ( 1 ± √(73) )/4, por lo que tienes dos opciones:
a)
x = ( 1 - √(73) )/4 ≅ -1,886;
b)
x = ( 1 + √(73 )/4 ≅ 2,386.
Espero haberte ayudado.
-
 Hola,¿ alguien podria hacer el apartado A y B? Es el rango de las siguientes matrices
Hola,¿ alguien podria hacer el apartado A y B? Es el rango de las siguientes matricesNo estoy seguro de que lo haya hecho bien. Gracias

César
el 7/8/19