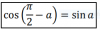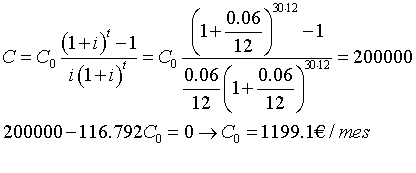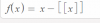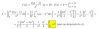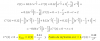Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Y3
el 16/12/18

Hola muy buenas profesor, quería saber cómo es posible este paso, no lo veo en ninguna fórmula del formulario que me mandaste. Perdona y muchas gracias por responder, agradezco mucho que existan personas como tú

••1 voto/s
•
Antonius Benedictus
el 16/12/18
El coseno de un ángulo coincide con el seno del complementario.

•1 voto/s
•
Antonius Benedictus
el 16/12/18

•1 voto/s
•

Cancelar
Isaac Gonzalez
el 16/12/18

Hola tengo un ejercicio que me gustaria saber como se resuelve. Dice asi: El banco te da un prestamo hipotecario de 200,000 euros el cual se paga a 30 años con un interes del 6% anual. La pregunta es, cuanto debo pagar al mes para pagar esos 200,000 euros mas cualquier interes que se haya acumulado?

••0 voto/s
•
César
el 16/12/18

•0 voto/s
•

Cancelar
Iman
el 16/12/18

Hola unicoos, tengo dudas hallando la continuidad de este ejericio f(x) = x^2+2 /x^2-2 , me podrían ayudar? Gracias.

••0 voto/s
•
Antonius Benedictus
el 16/12/18

•1 voto/s
•
Iman
el 16/12/18
Muchísimas gracias.

•0 voto/s
•

Cancelar
magui
el 15/12/18

Hola unicoos, me podrían ayudar con 1 ejercicio del 12 y 1 del 13, no entiendo como tengo que hallar la solución. Gracias

••0 voto/s
•
Antonius Benedictus
el 15/12/18
¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

•0 voto/s
•

Cancelar
Quiroga
el 15/12/18

¿Por qué esta función es par?
Entiendo la teoría, que si f(x)=-f(x) -> par, pero como la aplicaría a esta función?, en teoría sé que también es una función periódica.

••0 voto/s
•
Antonius Benedictus
el 15/12/18

•1 voto/s
•
Quiroga
el 15/12/18
Mil gracias de nuevo, y por si alguien más lo necesita dejo el vídeo el cual acabo de encontrar.

Función mantisa x-E(x)
•1 voto/s
•

Cancelar
Kevin
el 15/12/18

hola de nuevo, como se haría el limite cuando n tiende a infinito de la raíz enésima de n factorial . gracias de antemano

••0 voto/s
•
Antonius Benedictus
el 15/12/18

•0 voto/s
•

Cancelar
Y3
el 15/12/18

Hola, he intentado hacer estos ejercicios y no pillo por dónde van el c, el g, el h y el i. Por fa ayuda que ya estoy en la recuperación, gracias. (si hay algún video que lo explique me vendría bien)

••0 voto/s
•
Antonius Benedictus
el 15/12/18
El c)
Te mando un formulario:

•1 voto/s
•
Antonius Benedictus
el 15/12/18

•1 voto/s
•

Cancelar
Marta
el 15/12/18

Hola, me podrían ayudar a resolver esto:

••0 voto/s
•
Antonius Benedictus
el 15/12/18

•0 voto/s
•

Cancelar
María Florencia Suares
el 15/12/18

Hola yo necesito saber cómo sacar los puntos críticos de esta función

C(t)= 0,12t.e^(-t/2)

••1 voto/s
•
Antonius Benedictus
el 15/12/18

•1 voto/s
•

Cancelar
Telmiyo
el 15/12/18

Alguien me podría ayudar a responder esto: Porque utiliza el cambio de variable??

••0 voto/s
•
Antonio Silvio Palmitano
el 15/12/18
Emplear un cambio de variable es una forma de hacer el ejercicio, pero no es la única.
Tienes la integral:
I = ∫ (x/2^x)*dx = ∫ x*2^-x*dx;
aquí planteas el Método de Integración por Partes, y queda:
f(x) = x, de donde tienes: f ' (x) = 1,
g ' (x) = 2^-x, de donde tienes: g(x) = 2^-x/(-1*ln2) = -2^-x/ln2;
luego, aplicas el método y la integral queda:
I = x*(-2^-x/ln2) - ∫ (-2^-x/ln2)*1*dx;
luego, resuelves el signo en el primer término, resuelves y extraes factores constantes en el segundo término, y queda:
I = -x*2^-x/ln2 + (1/ln2) * ∫ 2^-x*dx;
luego, resuelves la integral en el segundo término (observa que ya la tienes resuelta en el planteo de la integración por partes del paso anterior), y queda:
I = -x*2^-x/ln2 + (1/ln2) * (-2^-x/ln2) + C;
luego, resuelves signos y factores numéricos en el segundo término, y queda:
I = -x*2^-x/ln2 - (1/(ln2)²)*2^-x + C.
Espero haberte ayudado.

•0 voto/s
•

Cancelar