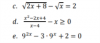Tienes la expresión de la cantidad de artículos producidos por hora en función de la cantidad de trabajadores:

P(x) = 38x - x² - 36 (1),

cuyo dominio es el conjunto de los números naturales no nulos.

Luego, tienes la cantidad de artículos a producir en este único pedido: 72000.

Tienes planteada la expresión de la cantidad de horas de trabajo necesarias: H(x).

(a)

Tienes el monto de costo fijo: F = 5000 euros (2).

(b)

Tienes el gasto promedio de materia prima por artículo: 1 euro, por lo que el gasto para todo el periodo queda:

M = 1*72000 = 72000 euros (3).

(c)

Tienes el salario por hora de cada trabajador: 10 euros, por lo que el gasto total en salarios queda:

S(x) = 10x*H(x) (4).

(i)

Puedes plantear para la cantidad de artículos que se deben producir:

P(x)*H(x) = 72000,

divides por P(x) en ambos miembros, y queda:

H(x) = 72000/P(x),

sustituyes la expresión señalada (1), y queda:

H(x) = 72000/(38x - x² - 36) (5).

(ii)

Puedes plantear que el costo de producción del pedido es la suma de los gastos, y queda:

C(x) = F + M + S(x),

sustituyes expresiones señaladas (2) (3) (4), y queda:

C(x) = 5000 + 72000 + 10x*H(x),

reduces términos numéricos, sustituyes la expresión señalada (5) y resuelves el último término, y queda:

C(x) = 77000 + 720000x/(38x - x² - 36) (6).

(iii)

Derivas la expresión remarcada y señalada (6), y queda:

C ' (x) = ( 720000*(38x - x² - 36) - 720000x*(38 - 2x) )/(38x - x² - 36)² (7),

planteas la condición de punto estacionario (posible máximo o posible mínimo, y queda:

C ' (x) = 0,

sustituyes la expresión señalada (7), y queda:

( 720000*(38x - x² - 36) - 720000x*(38 - 2x) )/(38x - x² - 36)² = 0,

multiplicas en ambos miembros por (38x - x² - 36)², y queda:

720000*(38x - x² - 36) - 720000x*(38 - 2x) = 0,

divides por 720000 en todos los términos de la ecuación, y queda:

38x - x² - 36 - x*(38 - 2x) = 0,

distribuyes el agrupamiento, y queda:

38x - x² - 36 - 38x + 2x² = 0,

reduces términos semejantes (observa que tienes cancelaciones), ordenas términos, y queda:

x² - 36 = 0,

sumas 36 en ambos miembros de la ecuación, y queda

x² = 36,

extraes raíz cuadrada en ambos miembros (observa que elegimos la raíz positiva), y queda:

x = 6 trabajadores;

luego, reemplazas este último valor remarcado en las expresiones señalada (6) (5), y queda:

C(6) = 77000 + 720000*6/(38*6 - 6² - 36),

resuelves, y queda:

C(6) ≅ 104692,31 euros,

que es el valor del costo mínimo de producción;

H(6) = 72000/(38*6 - 6² - 36),

resuelves, y queda:

H(6) ≅ 461,54 horas.

(iv)

Derivas la expresión remarcada y señalada (5), y queda:

H ' (x) = -72000*(38 - 2x)/(38x - x² - 36)² (8),

planteas la condición de punto estacionario (posible máximo o posible mínimo, y queda:

H ' (x) = 0,

sustituyes la expresión señalada (8), y queda:

-72000*(38 - 2x)/(38x - x² - 36)² = 0,

multiplicas en ambos miembros por (38x - x² - 36)², y queda:

-72000*(38 - 2x) = 0,

divides por -72000 en todos los términos de la ecuación, y queda:

38 - 2x = 0,

restas 38 en ambos miembros de la ecuación, y queda

-2x = -38,

divides por -2 en ambos miembros, y queda:

x = 19 trabajadores;

luego, reemplazas este último valor remarcado en las expresiones señalada (6) (5), y queda:

C(19) = 77000 + 720000*19/(38*19 - 19² - 36),

resuelves, y queda:

C(19) ≅ 119092,31 euros,

que es el valor del costo de producción con el tiempo mínimo;

H(19) = 72000/(38*19 - 19² - 36),

resuelves, y queda:

H(19) ≅ 221,54 horas,

que es el valor del tiempo mínimo de producción.

Espero haberte ayudado.

Por favor sube una foto con el enunciado para que podamos ayudarte.

Estos 3

c)

Tienes la ecuación:

√(2x+8) - √(x) = 2, sumas √(x) en ambos miembros, y queda:

√(2x+8) = √(x) + 2, elevas al cuadrado en ambos miembros, y queda:

( √(2x+8) )² = ( √(x) + 2 )², simplificas el primer miembro, desarrollas el segundo miembro, y queda:

2x + 8 = x + 4√(x) + 4, restas x y restas 4 en ambos miembros, y queda:

x + 4 = 4√(x), elevas al cuadrado en ambos miembros, y queda:

( x + 4 )² = ( 4√(x) )², desarrollas el primer miembro, resuelves el segundo miembro, y queda:

x² + 8x + 16 = 16x, restas 16x en ambos miembros, y queda:

x² - 8x + 16 = 0, factorizas el trinomio cuadrado perfecto en el primer miembro, y queda:

(x - 4)² = 0, extraes raíz cuadrada en ambos miembros, y queda:

x - 4 = 0, sumas 4 en ambos miembros, y queda:

x = 4,

y puedes verificar que la solución remarcada es válida si reemplazas y resuelves en la ecuación de tu enunciado.

Espero haberte ayudado.

e)

Tienes la ecuación:

9^2x -3*9^x + 2 = 0;

luego, puedes plantear la sustitución (cambio de incógnita):

9^x = w (1) (observa que w toma valores positivos),

de donde tienes:

9^2x = (9^x)² = 9^2x = w²;

luego, sustituyes las expresiones remarcadas en la ecuación, y queda:

w² - 3*w + 2 = 0,

que es una ecuación polinómica cuadrática, cuyas solucione son:

1)

w = 1, que al reemplazar en la ecuación señalada (1), queda:

9^x = 1, expresas el segundo miembro como una potencia con base 9, y queda:

9^x = 9⁰, por igualdad entre potencias con bases iguales, queda:

x = 0;

2)

w = 2, que al reemplazar en la ecuación señalada (1), queda:

9^x = 2, extraes logaritmos (elegimos los logaritmos naturales) en ambos miembros, y queda:

ln(9^x) = ln(2), aplicas la propiedad del logaritmo de una potencia, y queda:

x*ln(9) = ln(2), divides por ln(9) en ambos miembros, y queda:

x = ln(2)/ln(9).

Espero haberte ayudado.

d)

Tienes la inecuación:

(x² - 2x + 4)/(x - 4) - x ≥ 0, sumas x en ambos miembros, y queda:

(x² - 2x + 4)/(x - 4) ≥ x;

luego, tienes dos opciones, según sea el signo de la expresión del denominador del primer miembro:

1)

Si x - 4 > 0, que corresponde a: x > 4 (1),

entonces multiplicas por (x - 4) en ambos miembros (observa que no cambia la desigualdad), y queda:

x² - 2x + 4 ≥ x*(x - 4), distribuyes el segundo miembro, y queda:

x² - 2x + 4 ≥ x² - 4x, restas x², sumas 4x y restas 4 en ambos miembros (observa que tienes cancelaciones), y queda:

2x ≥ -4, divides por 2 en ambos miembros, y queda:

x ≥ -2 (2);

luego, teniendo en cuenta las condiciones expresadas en las inecuaciones señaladas (1) (2) (que deben verificarse en forma simultánea), tienes que para esta opción queda el subintervalo:

I₁ = (4,+∞);

2)

Si x - 4 < 0, que corresponde a: x < 4 (3),

entonces multiplicas por (x - 4) en ambos miembros (observa que sí cambia la desigualdad), y queda:

x² - 2x + 4 ≤ x*(x - 4), distribuyes el segundo miembro, y queda:

x² - 2x + 4 ≤ x² - 4x, restas x², sumas 4x y restas 4 en ambos miembros (observa que tienes cancelaciones), y queda:

2x ≤ -4, divides por 2 en ambos miembros, y queda:

x ≤ -2 (4);

luego, teniendo en cuenta las condiciones expresadas en las inecuaciones señaladas (3) (4) (que deben verificarse en forma simultánea), tienes que para esta opción queda el subintervalo:

I₂ = (-∞,-2].

Luego, planteas que el intervalo solución es la unión de los dos subintervalos remarcados, y queda:

S = (-∞,-2] ∪ (4,+∞).

Espero haberte ayudado.

a)

Observa que se cumplen las hipótesis de Teorema Fundamental del Cálculo Integral, por lo que aplicas el teorema, y la expresión de la función derivada queda:

F ' (x) = f(x) + x² + x³.

b)

Luego, tienes en tu enunciado que la abscisa del punto en estudio es:

x₀ = 1;

luego, evalúas la expresión de la función F para este valor, y queda:

F(1) = ₀∫¹ ( f(t) + t² + t³ )*dt,

separas en términos, y queda:

F(1) = ₀∫¹ f(t)*dt + ₀∫¹ t²*dt + ₀∫¹ t³*dt,

reemplazas el valor del primer término que tienes en tu enunciado, integras los dos últimos términos (observa que indicamos con corchetes de debes evaluar con Regla de Barrow), y queda:

F(1) = 1 + [t³/3] + [t⁴/4],

evalúas los dos últimos términos, y queda:

F(1) = 1 + 1/3 + 1/4,

resuelves, y queda:

F(1) = 19/12.

Luego, evalúas la expresión de la función derivada señalada (1) para la abscisa del punto en estudio, y queda:

F ' (1) = f(1) + 1² + 1³, 

reemplazas el valor del primer término que tienes en tu enunciado, resuelves los demás términos, y queda:

F ' (1) = 1 + 1 + 1,

resuelves, y queda:

F ' (1) = 3.

Luego, planteas la ecuación de la recta tangente en forma genérica, y queda:

y = F ' (x₀) * (x - x₀) + F(x₀),

reemplazas el valor de la abscisa del punto en estudio, y queda:

y = F ' (1) * (x - 1) + F(1),

reemplazas los valores de la función derivada evaluada y del la función evaluada, y queda:

y = 3*(x - 1) + 19/12;

distribuyes el primer término, y queda:

y = 3*x - 3 + 19/12,

reduces términos numéricos, y queda:

y = 3*x - 17/12,

que es la ecuación de la recta tangente a la gráfica de la función F que piden en tu enunciado.

Espero haberte ayudado.

b) La función es continua en todo su dominio.

Donde podría tener problemas es en el 15 y en el 11:

En t=15 es continua pues existe la imagen y coincide con los límites laterales

En t=11 no se anula el denominador.

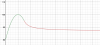
c) Durante lo 10 primeros meses el precio aumenta para luego disminuir.

El precio máximo se alcanza a los 10 meses con un importe de 100€ y el mínimo el día de su lanzamiento con 80€

d) Nunca bajará de 87€

Progresiones geométricas

Puedes considerar la caída inicial, por lo que al tocar el suelo la primera vez ha recorrido:

d₀ = 88 (en dm).

Luego, observa que de ahora en más la pelota "sube y vuelve a bajar" antes de volver a tocar el suelo.

Luego, sube hasta 2/3 partes de altura anterior ( h = (2/3)*88 = (2/3)¹*88 ) y luego vuelve a bajar, por lo que al tocar el suelo nuevamente ha agregado el recorrido:

d₁ = 2*(2/3)¹*88 (en dm).

Luego, sube hasta 2/3 partes de altura anterior ( h = (2/3)*(2/3)¹*88 = (2/3)²*88 ) y luego vuelve a bajar, por lo que al tocar el suelo nuevamente ha agregado el recorrido:

d₂ = 2*(2/3)²*88 (en dm).

Luego, sube hasta 2/3 partes de altura anterior ( h = (2/3)*(2/3)²*88 = (2/3)³*88 ) y luego vuelve a bajar, por lo que al tocar el suelo nuevamente ha agregado el recorrido:

d₃ = 2*(2/3)³*88 (en dm).

Luego, sube hasta 2/3 partes de altura anterior ( h = (2/3)*(2/3)³*88 = (2/3)⁴*88 ) y luego vuelve a bajar, por lo que al tocar el suelo nuevamente ha agregado el recorrido:

d₄ = 2*(2/3)⁴*88 (en dm).

Luego, puedes inferir que el recorrido agregado nuevamente en la "subida y bajada" número k es:

d_k = 2*(2/3)^k*88 (en dm),

y observa que la expresión remarcada es válida desde el agregado de recorrido número 1 en adelante.

Luego, puedes plantear la expresión del recorrido total, con n "subidas y bajadas":

d = d₀ + d₁ + d₂ + d₃ + d₄ + .... + d_n (observa que tienes n+1 términos, y que la pelota ha tocado el suelo n+1 veces),

sustituyes expresiones, y queda:

d = 88 + 2*(2/3)¹*88 + 2*(2/3)²*88 + 2*(2/3)³*88 + 2*(2/3)⁴*88 + ... + 2*(2/3)ⁿ*88,

extraes factores comunes entre todos los términos remarcados, y queda:

d = 88 + 2*(2/3)¹*88*( 1 + (2/3)¹ + (2/3)² + (2/3)³ + ... + (2/3)^n-1 ),

luego, observa que los términos remarcados del agrupamiento conforman una progresión geométrica cuyo primer elemento es 1 y cuya razón es 2/3 (observa que su valor absoluto es estrictamente menor que 1), por lo que sustituyes a todo el agrupamiento por la expresión de la suma geométrica, y queda:

d = 88 + 2*(2/3)¹*88*( ( 1-(2/3)ⁿ ) / (1-2/3) ), 

resuelves el coeficiente en el último factor, y queda:

d = 88 + 2*(2/3)¹*88*( ( 1-(2/3)ⁿ ) * 3,

extraes factor común (88), y queda:

d = 88*( 1 + 2*(2/3)¹*( ( 1-(2/3)ⁿ ) * 3 ),

resuelves el coeficiente en el segundo término del agrupamiento, y queda:

d = 88*( 1 + 4*( 1 - (2/3)ⁿ ) (en dm),

y recuerda que la expresión remarcada es válida a partir de n = 1.

Espero haberte ayudado.

Éste es parecido:

Muchas gracias, mucho más claro

Tienes que recordar las identidades trigonométricas y a partir de ahí realizar el cambio de variable.

Espero haberte ayudado, un saludo.