logo_unicoos

Foro de preguntas y respuestas de Matemáticas

logo beUnicoos
Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.
Ir a beUnicoos

  • icon

    Paula Sánchez
    el 12/3/18

    Hola me podrían decir dónde he fallado en el apartado C)  ya que la recta es y=2x +1

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio
    el 12/3/18

    Te paso la gráfica de la función, seguro que te ayuda:


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    poco
    icon

    Antonio Silvio Palmitano
    el 12/3/18

    Tienes la expresión de la función cuyo dominio es R:

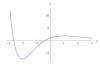
    f(x) = (x2+3x+1)*e-x (1),

    cuya función derivada tiene la expresión:

    f ' (x) = (2x+3)*e-x - (x2+3x+1)*e-x, extraes factor común, y queda:

    f ' (x) = ( 2x+3 - (x2+3x+1) )*e-x, distribuyes y reduces términos semejantes en el primer factor, y queda:

    f ' (x) = (-x2-x+2)*e-x (2) y observa que la función derivada está definida en todo el dominio de la función.

    C)

    Tienes la abscisa del punto en estudio: x = 0,

    luego evalúas las expresiones señaladas (1) (2) para este valor, y queda:

    f(0) = 1, que es la ordenada del punto en estudio, que queda expresado: A(0,1);

    f ' (0) = 2, que es la pendiente de la recta tangente en el punto en estudio;

    luego, con las coordenadas del punto y con el valor de la pendiente, puedes plantear la ecuación cartesiana punto-pendiente de la recta tangente:

    y = 2*(x - 0) + 1, cancelas el término nulo en el agrupamiento, y queda:

    y = 2*x + 1, que es la ecuación cartesiana explícita de la recta tangente que te piden en el enunciado.

    Espero haberte ayudado.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    bastante
  • icon

    jorge velazquez
    el 12/3/18

    como podria demostrar que

    det(kA)=kndet(A) CON K REAL 

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 12/3/18

    La matriz kA se construye multiplicando por k todos los elementos de A, con lo que cada una de las "n" filas de A queda multiplicada por k.

    Entonces, al hacer el determinante, sacamos un factor k de cada una de las "n" filas. Por ello, queda k^n *det(A)

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    jorge velazquez
    el 12/3/18

    Antonio y por induccion matemática como seria


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
    icon

    Antonius Benedictus
    el 12/3/18

    No es necesario aplicar el método de inducción. Es más, creo que aplicarlo a esto complica las cosas.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo

  • Usuario eliminado
    el 12/3/18

    Hola buenas, como podría demostrar estas dos matrices? a) (A^-1)^-1=A b) (λ·A)^-1=B^-1·A^-1. Muchísimas gracias por la ayuda. 

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 12/3/18


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    suficiente
  • icon

    Paula Sánchez
    el 12/3/18

    holaaa¡¡

    no entiendo por que b lo iguala a 0 para que sea finito y sin embargo el a lo iguala a 1

    reply•thumb_up•0 voto/s•flag
    icon

    David Poyatos
    el 12/3/18

    A es igual a 1/2 porque al hacer el limite te queda una ecuación y el valor de a es la solución de dicha ecuación. Y b lo iguala a 0 para que de un número finito y no infinito.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    suficiente
  • icon

    Paula Sánchez
    el 12/3/18

    buenas tardessss¡¡


     por que se iguala b a 0 para que esta sea un numero finito??


    reply•thumb_up•0 voto/s•flag
    icon

    David Poyatos
    el 12/3/18

    Porque si b no fuera cero, no te quedaría la indeterminación (0/0), sino que te quedaría: (número/0); que hace que el límite sea infinito y no finito e igual a 1.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    poco
  • icon

    ayal24
    el 12/3/18

    Buenas tardes, Me podríais ayudar a resolver la integral de 3xe1-x^2   

    Muchas gracias.

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 12/3/18

    Vamos con una orientación.

    Puedes aplicar la sustitución (cambio de variable):

    w = 1 - x2, de donde tienes:

    dw = -2*x*dx, y también tienes: -(1/2)*dw = x*dx.

    Haz el intento de resolver la integral, y si te resulta necesario, no dudes en volver a consultar.

    Espero haberte ayudado.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    bastante
  • icon

    Sheila
    el 12/3/18

    Hola, me podeis ayudar con este ejercicio:


    reply•thumb_up•0 voto/s•flag
    icon

    David Poyatos
    el 12/3/18

    Esta es la respuesta a tu ejercicio:

    Espero haberte ayudado

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    Antonio Silvio Palmitano
    el 12/3/18

    a)

    Plantea la expresión de la pendiente de la recta, de la que tienes dos puntos (-1,2) y (3,-2):

    m = (y2-y1)/(x2-x1) = (-2-2)/(3+1) = -4/4 = -1;

    luego, con el primero de los puntos y la pendiente, planteas la ecuación punto-pendiente:

    y = m*(x-x1)+y1, reemplazas datos, y queda:

    y = -1*(x+1)+2, distribuyes el primer término, y queda:

    y = -x - 1 + 2, reduces términos numéricos, y queda:

    y = -x + 1, que es la ecuación cartesiana explícita de la recta.

    b)

    Tienes la recta cuya ecuación cartesiana explícita es: y = -2*x+3, cuya pendiente es: m = -2,

    que, por la condición de paralelismo, es la pendiente de la recta paralela cuya ecuación debes determinar,

    de la que además tienes el punto (2,3); luego, planteas la ecuación punto-pendiente, y queda:

    y = -2*(x-2)+3, distribuyes el primer término, y queda:

    y = -2*x + 4 + 3, reduces términos numéricos, y queda:

    y = -2*x + 7, que es la ecuación cartesiana explícita de la recta.

    c)

    Recuerda que las rectas paralelas al eje OX tienen ecuaciones cuya forma es: y = k,

    donde k es la ordenada de todos los puntos de la recta; luego, como tienes que el punto (3,-2),

    cuya ordenada es k = -2 pertenece a la recta, tienes que su ecuación cartesiana explícita es: y = -2.

    d)

    Tienes la pendiente de la recta: m = -2, y su ordenada al origen: b = 4;

    luego, planteas su ecuación cartesiana explícita: y = m*x+b,

    reemplazas valores, y queda:

    y = -2*x+4, que es la ecuación cartesiana explícita de la recta.

    Espero haberte ayudado.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Sergio Hueso
    el 12/3/18

    Hola , agradeceria muchisimo q me pudieses ayudar con los ejercicios: 32, 33 , 34 , 35 ,36, y 104 y 105. Muchisimas gracias.

    reply•thumb_up•0 voto/s•flag
    icon

    César
    el 12/3/18

    No es cosa de mandar ejercicios en masa Sergio, con cuales tienes dificultades??


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    Sergio Hueso
    el 12/3/18

    Con el ultimo que he mandado Cesar..


    Gracias

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Guim
    el 12/3/18

    Si en este  sistema de equaciones, multiplico la sagunda X por -2, para poder eliminar la X, despues, tendre que multiplicar el resultado por 2, o no hace falta?

    2x + 3y = 7

    x - 7y = 9  

                                                                                     

    reply•thumb_up•0 voto/s•flag
    icon

    Juan
    el 12/3/18

    Puedes multiplicar por -2 sin problemas, no hace falta ni se debe multiplicar el resultado después


    thumb_up•2 voto/s•flag
    1 2 3 4 5
    muchísimo