-
evaluación dela siguiente integral de linea mediante el teorema fundamental del cálculo para integrales de línea.
∫yzexy dx+xzexy dy +exy dz ; C:r(t)=(2t-1, t2-t , t) Con 0<t<1
Antonio Silvio Palmitano
el 12/3/18Observa que tienes la expresión desarrollada de una integral de línea de un campo vectorial F = <P,Q,R>, cuyas componentes son:
P = yzexy, Q = xzexy, R = exy,
y observa que las tres funciones son continuas y sus derivadas parciales primeras son continuas en R3;
luego, planteas la expresión del rotacional del campo vectorial, y queda:
rot(F) = ∇ x F = <Ry-Qz,Pz-Rx,Qx-Py> = < xexy-xexy , yexy-yexy , zexy-zexy > = <0,0,0>;
por lo tanto tienes que el campo vectorial es conservativo en R3, y admite función potencial.
Luego, te muestro una forma práctica para plantear la expresión de la función potencial:
recuerda que el gradiente de la función potencial es el campo conservativo, por lo que puedes plantear:
grad(g) = ∇g = F, sustituyes expresiones, y queda:
<gx,gy,gz> = <P,Q,R>,
luego, por igualdad entre expresiones vectoriales, tienes el sistema de ecuaciones diferenciales parciales (observa que sustituimos expresiones):
gx = yzexy, integras parcialmente con respecto a x, y queda: g = zexy + A(y,z), con la expresión de la función A a determinar;
gy = xzexy, integras parcialmente con respecto a y, y queda: g = zexy + B(x,z), con la expresión de la función B a determinar;
gz = exy, integras parcialmente con respecto a z, y queda: g = zexy + C(x,y), con la expresión de la función C a determinar;
luego, con los términos explícitos sin repetir, puedes proponer la expresión general de las funciones potenciales:
g(x,y,z) = zexy + C,
y observa que si derivas parcialmente con respecto a las variables x, y, z obtienes las respectivas expresiones de las componentes del campo vectorial.
Luego, tienes la expresión de la función vectorial paramétrica de posición de la trayectoria, cuyas componentes son funciones continuas en el intervalo paramétrico, por lo que evalúas en los extremos de este intervalo, y queda:
r(0) = <-1,0,0>, por lo que tienes que el punto inicial de la trayectoria es: A(-1,0,0);
r(1) = <1,0,1>, por lo que tienes que el punto final de la trayectoria es: B(1,0,1).
Luego, aplicas el Teorema Fundamental de las Integrales de Línea, y queda:
I = ∫C F•dr = [ g(x,y,z) ] = [ zexy ] = evalúas entre los puntos A y B = 0 - 1 = -1.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 12/3/18Recuerda la propiedad: "el determinante de un producto de matrices es igual al producto de los determinantes de las matrices".
Recuerda que el determinante de la matriz identidad es igual a uno.
Recuerda que una matriz es invertible si y solo si es cuadrada y su determinante es distinto de cero.
Luego, tienes las hipótesis:
A ∈ Rn*n, por lo que tienes que la matriz A es cuadrada de orden n, con elementos reales;
A es invertible, por lo tanto tienes: det(A) ≠ 0, y también tienes que existe su matriz inversa A-1.
Luego, como las matrices A y A-1 son inversas entre sí, puedes plantear (indicamos con I a la matriz identidad de orden n):
A*A-1 = I, por igualdad entre matrices tienes que los determinantes de ambos miembro son iguales, y queda:
det(A*A-1) = det(I), aplicas la propiedad del determinante de un producto de matrices en el primer miembro, y queda:
det(A)*det(A-1) = det(I), reemplazas el valor del determinante de la matriz identidad en el segundo miembro, y queda:
det(A)*det(A-1) = 1, observa que tienes que el primer factor en el primer miembro es distinto de cero, por lo que el segundo factor también lo es,
luego divides por det(A) en ambos miembros (recuerda que det(A) es distinto de cero), y queda:
det(A-1) = 1/det(A).
Espero haberte ayudado.
-
hola unicoos,tengo un problema de transformaciones lineales.
Hallar todos los a ∈ R para los cuales exista una transformación lineal f: R3→R3 que satisfaga:
f(1,-1,1)=(2,a,-1)
f(1,-1,2)=(a^2,-1,1)
f(1,-1,-2)=(5,-1,-7)
-
El volumen entre
x^2+y^2 ≤ 1
y ≥ 0
y ≥ x
0 ≤ z ≤ 1−x^2−y^2
da 3pi/16 según el solucionario, pero no llego a ese resultado, alguien me echa una mano?
Antonius Benedictus
el 11/3/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Antonio Silvio Palmitano
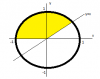
el 12/3/18Observa que en el gráfico está sombreada la región D del plano OXY que corresponde a la base del sólido.
Luego, observa que el sólido esta limitado superiormente por un paraboloide circular con eje OZ y vértice (0,0,1).
Luego, la expresión del volumen en coordenadas cartesianas queda:
V = ∫∫D ( (1-x2-y2) - 0 )*dx*dy = ∫∫D ( 1-(x2+y2) )*dx*dy.
Luego, puedes plantear el cambio a coordenadas polares:
x = r*cosθ,
y = r*senθ,
cuyo factor de compensación (Jacobiano) es: |J| = r,
y observa que la región de integración (base del sólido) queda expresada con los intervalos:
π/4 ≤ θ ≤ π,
0 ≤ r ≤ 1.
Luego, aplicas el cambio y la integral correspondiente al volumen del sólido queda:
V = π/4∫π0∫1 (1 - r2)*r*dr*dθ = π/4∫π0∫1 (r - r3)*dr*dθ =
resuelves la integral para la variable r (indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:
= π/4∫π [ r2/2 - r4/4 ]*dθ =evalúas = π/4∫π ( (1/2-1/4) - 0 )*dθ = (1/4) * π/4∫π 1*dθ =
resuelves la integral para la variable θ (indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:
= (1/4) * [ θ ] = evalúas = (1/4) * (π - π/4) = (1/4)*(3*π/4) = 3*π/16.
Espero haberte ayudado.
-
Antonius Benedictus
el 11/3/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
jorge velazquez
el 12/3/18No amigo has el cambio a coordenadas polares
X=rcosα
Y=rsenα
r^2= x^2 + y^2 luego si (x,y)->(0,0) entonces r->0
Luego
Lim(r->0)[((rcosα)-(rsenα ))^2]/((rcosα)^2 + (rsenα)^2)
Lim(r->0)[r^2(cosα -senα)^2]/(r^2)
Se Cancelan las r^2
Queda lim(r->0)(cosα -senα)^2= (cosα -senα)^2 luego el limite tiene distintos valores que dependen del ángulo y por definición el limite es único por tanto no existe
Y recuerda que
sen^2(α )+cos^2(α)=1
Hiciste mal tucambio a coordenadas polares
-
Antonius Benedictus
el 11/3/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Antonius Benedictus
el 11/3/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
jorge velazquez
el 12/3/18 -
Antonius Benedictus
el 11/3/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
jorge velazquez
el 12/3/18Antonio Silvio Palmitano
el 12/3/18Has planteado bien la sustitución (cambio de variable): z = xy, has sustituido correctamente, y el límite te ha quedado:
Lím(z→0) (cosz - 1)/z2 =
que es un límite indeterminado de una variable (observa que el numerador y el denominador tienden ambos a cero),
luego, multiplicas al numerador y al denominador por (cosz + 1), y queda:
= Lím(z→0) (cosz - 1)*(coz + 1) / z2*(cosz + 1) =
distribuyes en el numerador, luego cancelas términos opuestos, y queda:
= Lím(z→0) (cos2z - 1) / z2*(cosz + 1) =
extraes factor común -1 en el numerador, y queda:
= Lím(z→0) (-1)*(-cos2z + 1) / z2*(cosz + 1) =
aplicas la identidad del coseno en función del seno en el agrupamiento del numerador, y queda:
= Lím(z→0) (-1)*sen2z / z2*(cosz + 1) =
extraes el factor constante, expresas al argumento como producto de expresiones fraccionarias, y queda:
= -1 * Lím(z→0) (senz/z)*(senz/z)*( 1/(cosz+1) ) =
aplicas la propiedad del límite de un producto de funciones, y queda:
= -1 * Lím(z→0) (senz/z) * Lím(z→0) (senz/z) * Lím(z→0) ( 1/(cosz+1) ) =
resuelves (observa que en los dos primeros límites tienes que son iguales a uno), y queda:
= -1*1*1*(1/2) = -1/2.
Espero haberte ayudado.
-
Antonius Benedictus
el 11/3/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Antonio Silvio Palmitano
el 12/3/18Puedes multiplicar por x (observa que x tiende a cero pero no es igual a cero), y queda:
L = Lím( (x,y)→(0,0) ) x*(ex*y - 1)/(x*y),
aplicas la propiedad del límite de una multiplicación de funciones, y queda:
L = Lím( (x,y)→(0,0) ) x * Lím( (x,y)→(0,0) ) (ex*y - 1)/(x*y) = L1 * L2 (*);
luego, puedes plantear los dos límites por separado:
1)
L1 = Lím( (x,y)→(0,0) ) x = 0 (observa que es un límite directo);
2)
L2 = Lím( (x,y)→(0,0) ) (ex*y - 1)/(x*y),
aplicas la sustitución (cambio de variable): w = x*y (observa que w tiende a cero cuando x e y tienden a cero), y queda:
L2 = Lím(w→0) (ew - 1)/w = Lím(w→0) (ew - 1) / (w - 0) = Lím(w→0) (ew - e0) / (w - 0) (1);
luego, observa que la expresión remarcad y señalada (1) corresponde a la definición de la derivada de la función cuya expresión es:
g(w) = ew, cuya expresión es:
g ' (w) = ew, evaluada para w = 0,
por lo que tienes que la expresión remarcada y señalada (1) es igual a:
g ' (0) = e0 = 1 (2);
luego, reemplazas el valor señalado (2) en la expresión remarcada y señalada (1), y queda:
L2 = 1 (3).
Luego, reemplazas los valores del límite L1 que ya hemos calculado, y del límite L2 en al expresión señalada (*) y queda:
L = 0*1 = 0.
Espero haberte ayudado.
-
Antonius Benedictus
el 11/3/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Antonio Silvio Palmitano
el 12/3/18Vamos con una orientación.
Tienes un límite indeterminado, ya que tanto el numerador como el denominador de su argumento tienden a cero.
Luego, multiplicas por x al numerador y al denominador, y el límite queda:
Lím( (x,y)→(0,0) ) x*sen(x*y) / (x*y) =
aplicas la propiedad del límite de un producto de funciones, y queda:
= Lím( (x,y)→(0,0) ) x * Lím( (x,y)→(0,0) ) sen(x*y) / (x*y) =
observa que el primer límite es igual a cero, y observa que en el segundo puedes aplicar la sustitución (cambio de variable) w = x*y, y tienes que es igual a 1, por lo que tienes:
= 0*1 = 0.
Espero haberte ayudado.