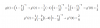-
hola de nuevo, alguien me podria ayudar? Gracias
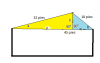
Una casa mide 45 pies del frente a la parte trasera. El techo mide 32 pies desde el frente de la casa hasta la cumbrera, y 18 pies desde la cumbrera a la parte trasera de la casa. Calcule los ángulos de elevación de las partes delantera y trasera del techo, y también la altura del techo.
Antonio Silvio Palmitano
el 11/3/18Observa el triángulo oblicuo formado por las dos figuras coloreadas, y observa que puedes plantear el Teorema del coseno para los ángulos de elevación α y β:
182 = 452 + 322 - 2*45*32*cosα,
322 = 452 + 182 - 2*45*18*cosβ,
y puedes despejar los valores de los cosenos de los ángulos de elevación, y de ahí obtener sus medidas.
Luego, observa los triángulos rectángulos coloreados, y puedes plantear:
h/32 = senα, multiplicas por 32 en ambos miembros, y queda: h = 32*senα (en el triángulo sombreado amarillo),
h/18 = senβ, multiplicas por 18 en ambos miembros, y queda: h = 18*senβ (en el triángulo sombreado celeste).
Espero haberte ayudado.
-
Me pueden resolver estos problemas:
1. El número de personas que acuden a una exposición en un día viene dado por la función p(t) = 12t – 2t2
, siendo t el tiempo que pasa desde la apertura, en horas. Si el horario de exposición es de 15 a 21 horas, ¿cuántas personas
visitan la exposición al día?
2.- Una fábrica arroja diariamente material contaminante a una balsa según un ritmo dado por la siguiente función:
m = 0,01t3 -0,2t2 + t + 1, siendo m la cantidad de material en kilogramos y t la hora del día. ¿Cuánto material arroja cada día?
Antonio Silvio Palmitano
el 11/3/181)
Si la expresión corresponde a la función ritmo de personas que ingresan a la exposición (consulta con tus docentes por el enunciado), observa que tienes que el lapso entre la apertura y el cierre es: 21 - 15 = 6 horas;
luego, plantea la expresión de la cantidad de personas que ingresaron a la exposición:
N = 0∫6 ( 12*t - 2*t2)*dt = integras = [ 12*t2/2 - 2*t3/3 ] = evalúas con Regla de Barrow = (6*62 - (2/3)*63) - (0 - 0) = (216 - 144) - 0 = 72 personas.
2)
Si consideramos que la fábrica funciona durante todo el día, entonces plantea para la masa de material arrojado a la balsa:
M = 0∫24 (0,01*t3 - 0,2*t2 + t + 1)*dt = integras = [ 0,01*t4/4 - 0,2*t3/3 + t2/2 + t ] = evalúas con Regla de Barrow:
= (829,44 - 921,6 + 288 + 24) - (0 - 0 + 0 + 0) = 219,84 - 0 = 219,84 Kg.
Espero haberte ayudado.
-
hola, alguien me podria ayudar con este problema? Gracias.
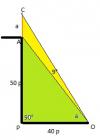
Una bandera está en la orilla de un acantilado de 50 pies de altura, en la orilla de un río de 40 pies de ancho. Un observador en la orilla opuesta del río mide un ángulo de 9 grados entre su visual a la punta del asta y su visual a la base del asta. Calcula la altura del asta.
Antonio Silvio Palmitano
el 11/3/18Observa el dibujo, y verás que O es el punto de observación, P es el punto del acantilado que está a nivel del suelo, A es el punto base del asta, y Ces su punto cumbre.
Luego observa que tienes dos triángulos rectángulos, y que llamamos a a la longitud del asta, y que llamamos α al ángulo determinado por el suelo y la visual del observador a la base del asta:
a)
Triángulo OPC, del que tienes:
x = 40 p (base), y = a + 50 p (altura, θ = α + 9° (medida del ángulo interior correspondiente al vértice O;
luego, puedes plantear:
y/x = tan(α + 9°), multiplicas en ambos miembros por x (observa que su valor es estrictamente positivo), y queda:
y = x*tan(α + 9°), sustituyes expresiones, y queda:
50 + a = 40*tan(α + 9°), restas 50 en ambos miembros, y queda:
a = 40*tan(α + 9°) - 50 (1).
b)
Triángulo OPA, del que tienes:
x = 40 p (base), y = 50 p (altura, α = a determinar (medida del ángulo interior correspondiente al vértice O;
luego, puedes plantear:
tan(α) = y/x, reemplazas valores, y queda:
tan(α) = 50/40 = 1,25, compones con la función inversa de la tangente, y queda:
α ≅ 51,340°.
Luego, reemplazas el valor remarcado en la ecuación señalada (1), y queda:
a ≅ 40*tan(60,340°) - 50, resuelves el primer término, y queda:
a ≅ 70,242 - 50, reduces términos semejantes, y queda:
a ≅ 20,242 pies.
Espero haberte ayudado.
-
* La mayoría de fenómenos físicos se miden empleando pruebas cuya fiabilidad no es total. Así, se emplea informalmente el concepto de ‘falso positivo’ si la prueba arroja un resultado positivo (detecta el fenómeno) cuando en realidad dicho fenómeno no tiene lugar. De forma análoga, se habla de ‘falso negativo’ si la prueba arroja un resultado negativo (no detecta el fenómeno) cuando en realidad dicho fenómeno sí tiene lugar. Suponga un determinado fenómeno que se da con una probabilidad p y que se mide con una prueba cuyas probabilidades de ‘falso positivo’ y ‘falso negativo’ son α y β, respectivamente. Se pide:
1. Probabilidad de que la prueba detecte el fenómeno si ´este ocurre en realidad.
2. Probabilidad de que el fenómeno no ocurra y la prueba lo detecte.
3. Probabilidad de que el fenómeno no ocurra y la prueba no lo detecte.
4. Probabilidad de que la prueba detecte el fenómeno.
5. Probabilidad de que no ocurra el fenómeno en realidad aunque la prueba lo ha detectado.
-
El motor de un tractor tiene una componente de acero con base circular modelada por la función vectorial siguiente r(t)=2cos(t) î +2 sen(t) j Si la altura está dada por z=1+y2 Todas las medidas están dadas en centímetros.
a)Encontrar el área superficial lateral de la componente.
b)La componente está en forma de una capa de un grosor de 0.2cm Determinar de acuerdo al inciso anterior la cantidad de acero usado en la producción de la componente.
Antonio Silvio Palmitano
el 11/3/18Tienes la expresión de la función altura: f(x,y) = 1 +y2;
y para plantearla en cada punto de la curva base (observa que se trata de una circunferencia cuyo radio es 2 y su centro es el origen de coordenadas), sustituyes las componentes de la función vectorial de posición (x = 2*cost, y = 2*sent), y queda:
f( r(t) ) = 1 + ( 2*sent )2 = 1 + 4*sen2t.
Luego, plantea la expresión del diferencial de arco de la curva base:
ds = |r ' (t)|*dt = |<-2*sent,2*cost>|*dt = 2*|<-sent,cost>| = 2*√( (-sent)2 + cos2t) ) = 2*√(sen2t + cos2t) = 2*√(1) = 2*1 = 2.
Luego, puedes plantear la expresión del área lateral de la pieza.
A = ∫C f(x,y)*ds = 0∫2π f( r(t) )*|r ' (t)|*dt = sustituyes expresiones:
= 0∫2π ( 1 + 4*sen2t ) )*2*dt = 2 * 0∫2π ( 1 + 4*sen2t )*dt = ...,
y puedes continuar la tarea por medio de la sustitución trigonométrica: sen2t = ( 1 - cos(2t) )/2.
Luego, tienes el espesor de la pieza (e = 0,2 cm), y puedes calcular su volumen multiplicándolo por el área que has calculado en el inciso anterior.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 11/3/18Efectivamente, es tal cuál dices.
La expresión de las infinitas soluciones del sistema de tres ecuaciones con cuatro incógnitas que propones es la correcta, y observa que para cada número real puedes determinar la ecuación de una curva que pasa por los tres puntos que tienes en tu enunciado, y observa que al conjunto de las infinitas curvas es a lo que llaman "familia de curvas".
Espero haberte ayudado.
-
Se consulta a 15000 personas la programacion de dos canales de tv. A 2320 solo le gustan los programas del canal 3, y de la 6580 manifiesta elegir canal 4,
2000 dijeron que le gustaba tambien algunos programas del canal 3.
A-¿cuantas personas solo ve canal 4?
B- ¿cuantas personas manifiesta ver programa del canal 3?
C- ¿ a cuantas personas encuestada no le gusta la programacion de ninguno de los canale?