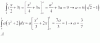-
-
UNA CONSULTA SOBRE ESTA INTEGRAL.
∫(e^(√X) +1)/√X=
yo hice t= e^(√X) → dx=(2√X)/e^(√X)dt
reemplace integre y me dio esto: 2(t +ln |t|)+c ( no reemplazo xq se entiende menos)
pero en el modulo la respuesta me sale : 2t+2√X +c
esta bien lo que hice o no?Antonio Silvio Palmitano
el 23/2/18Plantea la sustitución (cambio de variable:
w = √(x) (1),
de donde tienes:
dw = dx/( 2√(x) ), sustituyes la expresión señalada (1), y queda:
dw = dx/(2w), haces pasaje de divisor como factor, y queda:
2w*dw = dx (2).
Luego, planteas la integral de tu enunciado, y queda:
I = ∫ ( e√(x) + 1)/√(x) )*dx, sustituyes las expresiones señaladas (1) (2), y queda:
I = ∫ (ew + 1)*2w*dw, distribuyes en el argumento de la integral, y queda:
I = ∫ (ew*2w + 2w)*dw, separas la integral en término, extraes factores constantes, y queda:
I = 2*∫ (ew*w*dw + 2*∫ w*dw;
luego, observa que puedes resolver la primera integral por medio del Método de Integración por Partes (planteas: u = w, dv = ew*dw, y te dejo la tarea), y que la segunda integral se resuelve en forma directa, por lo que resuelves, y queda:
I = 2*(w*ew- ew) + w2 + C = 2*(w - 1)*ew + w2 + C;
luego, sustituyes la expresión señalada (1), simplificas potencia y raíz en el segundo término, y queda:
I = 2*(√(x) - 1)*e√(x) + x + C.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 23/2/18Observa que tienes un sistema de cuatro ecuaciones con tres incógnitas, y observa que es homogéneo, por lo que es compatible.
Luego, planteas la matriz ampliada del sistema, y queda:
1 -2 a 0
0 -a 2 0
2 -1 a+1 0
1 1 1 0
Permutas la primera y la cuarta fila, y queda:
1 1 1 0
0 -a 2 0
2 -1 a+1 0
1 -2 a 0
Permutas la segunda y la cuarta fila, y queda:
1 1 1 0
1 -2 a 0
2 -1 a+1 0
0 -a 2 0
A la segunda fila le restas la primera, a la tercera fila le restas el doble de la primera fila, y queda:
1 1 1 0
0 -3 a-1 0
0 -3 a-1 0
0 -a 2 0
A la tercera fila le restas la segunda fila, y queda:
1 1 1 0
0 -3 a-1 0
0 0 0 0
0 -a 2 0
Permutas la tercera fila con la cuarta, y queda:
1 1 1 0
0 -3 a-1 0
0 -a 2 0
0 0 0 0
Luego, plantea dos casos;
1°)
a = 0, reemplazas y la matriz ampliada queda:
1 1 1 0
0 -3 -1 0
0 0 2 0
0 0 0 0;
y observa que la matriz escalonada del sistema tiene rango 3, y como coincide con el número de incógnitas, tiene que su solución única es: x = 0, y = 0, z = 0;
2°)
a ≠ 0,
planteas el determinante de la matriz del sistema, y queda:
D =
1 1 1
0 -3 a-1
0 -a 2
desarrollas el determinante según su primera columna, y queda:
D = 1*( -3*2 - (-a)*(a-1) ), distribuyes, ordenas términos, y queda:
D = a2 - a - 6, factorizas la expresión (observa que es polinómica cuadrática cuyas raíces son -2 y 3), y queda:
D = (a + 2)*(a - 3);
luego, tienes otros tres casos:
a)
a ≠ -2 y a ≠ 3, que corresponde a: D ≠ 0 y el sistema es compatible determinado con solución única;
b)
a = -2,
sustituyes en la matriz ampliada escalonada, y queda:
1 1 1 0
0 -3 -3 0
0 2 2 0
0 0 0 0
a la tercera fila le sumas la segunda fila multiplicada por 2/3, y queda:
1 1 1 0
0 -3 -3 0
0 0 0 0
0 0 0 0
y observa que la matriz escalonada del sistema y la matriz escalonada ampliada tienen rango 2, que no coincide con el número de incógnitas, por lo que tienes que el sistema es compatible indeterminado y admite infinitas soluciones;
c)
a =3,
reemplazas en la matriz ampliada escalonada, y queda:
1 1 1 0
0 -3 2 0
0 -3 2 0
0 0 0 0
a la tercera fila le restas la segunda fila, y queda:
1 1 1 0
0 -3 2 0
0 0 0 0
0 0 0 0
y observa que la matriz escalonada del sistema y la matriz escalonada ampliada tienen rango 2, que no coincide con el número de incógnitas, por lo que tienes que el sistema es compatible indeterminado y admite infinitas soluciones.
Luego, queda que plantees los sistemas de ecuaciones en cada caso, los resuelvas y expreses las soluciones, o solución, según corresponda.
Espero haberte ayudado.
-
Hola a todos, donde puedo ver "operaciones con números decimales". Quiero explicárselo a mi hermano pequeño y querría ver un video didáctico sobre suma , resta, multiplicación y división de números decimales.
Gracias!!!!
-
a2-b2-3ab para a=2 b=1/2
Por que me da -3/4 que hago mal?? En el libro la solución es 3/4 sin el menos.
Antonio Silvio Palmitano
el 23/2/18Tienes la expresión:
a2 - b2 - 3*a*b = reemplazas valores:
= (2)2 - (1/2)2 - 3*(2)*(1/2) = resuelves términos:
= 4 - 1/4 - 3 = multiplicas y divides por 4 en el primero y en el último término, y queda:
= 4*4/4 - 1/4 - 3*4/4 = resuelves los numeradores en el primero y en el tercer término, y queda:
= 164 - 1/4 - 12/4 = extraes denominador común:
= (16 - 1 - 12)/4 = resuelves el numerador, y queda:
= 3/4.
Espero haberte ayudado.
-
Se que no soy el único que necesita ayuda, si no fuera mucho me podrían dar alguna pista. ¡GRACIAS UNICOOS!
-
Buenos días. Debajo de los videos está la opción de "material adicional" y dentro de están varios archivos, uno de los cuales es la teoría. Dentro del archivo de la teoría hay actividades con cuestiones y preguntas que no están resueltas. Me podría alguien decir donde están las soluciones a esas cuestiones y problemas ? Muchas gracias