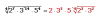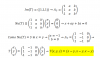-
Antonio Silvio Palmitano
el 22/2/18Comienza por expresar a las potencias como productos con algunos factores cuyos exponentes sean múltiplos de cuatro:
29 = 22*4+1 = 22*4*21 = (22)4*21,
313 = 33*4+1 = 33*4*31 = (33)4*31;
luego, tienes la expresión de tu enunciado:
4√(29*313) = sustituyes las expresiones de los factores en el argumento de la raíz:
= 4√( (22)4*21 * (33)4*31 ) = ordenas factores en el argumento de la raíz, y queda:
= 4√( (22)4*(33)4*21*31 ) = distribuyes la raíz entre los dos primeros factores, y el producto de los dos últimos, y queda:
= 4√( (22)4 ) * 4√( (33)4 ) * 4√( 21*31 ) = simplificas índices y exponentes en los dos primeros factores, y queda:
= 22*33*4√( 21*31 ).
Espero haberte ayudado.
-
-
Buenas tardes, ¿me podrían ayudar con estas integrales indefinidas?
1- ∫ (x-1) / (2x ) dx
2 - ∫ (sin2x + 1) / (cos2x + 1) dx
Muchas gracias.Antonio Silvio Palmitano
el 21/2/18Vamos con una orientación para el primero.
Expresas el argumento de la integral como un producto, y queda:
I = ∫ (x-1)*2-x*dx = distribuyes = ∫ x*2-x*dx - ∫ 2-x*dx;
y observa que en la primera integral puedes aplicar el Método de Integración por Partes,
con: u = x, du = dx, dv = 2-x*dx, v = -2-x;
y observa que la segunda integral es directa.
Luego, puedes terminar la tarea.
Espero haberte ayudado.
-
Pregunta de trigonometría de cuarto de eso.
¿Cómo se haría este ejercicio?
Traduzco: Alfa y beta son complementarios. Demuestra que tangente de beta = 1 / tangente de alfa.
Si tangente de alfa = 3/4, calcula sin de beta, cos de beta y tangente de beta.

Antonio Silvio Palmitano
el 21/2/18Seguramente, tienes vistas en clase las identidades para ángulos complementarios:
senβ = cosα (1),
cosβ = senα (2);
y también las identidades elementales:
tanx = senx/cosx (3),
cotgx = cosx/senx (4),
cotgx = 1/tanx (5).
luego, planteas la expresión de la tangente del ángulo β en función de su seno y de su coseno, y queda:
tanβ = senβ/cosβ = sustituyes las expresiones señaladas (1) (2):
= cosα/senα = sustituyes la expresión señalada (4):
= cotgα = sustituyes la expresión señalada (5):
= 1/tanα.
Luego, tienes el dato: tanα = 3/4;
luego, aplicas la identidad demostrada en el inciso anterior, y queda:
tanβ = 1/tanα = 1/(3/4) = 4/3.
Luego, aplicas la identidad señalada (3) para expresar el dato, planteas la identidad fundamental, y queda el sistema de ecuaciones:
senα/cosα = 3/4, aquí haces pasaje de divisor como factor, y queda: senα = (3/4)cosα (6),
cos2α + sen2α = 1;
luego, sustituyes la ecuación señalada (6) en la segunda ecuación, resuelves el segundo término, y queda
cos2α + (9/16)cos2α = 1, reduces términos semejantes, y queda
(25/16)cos2α = 1, multiplicas por 16/25 en ambos miembros de la ecuación, y queda:
cos2α = 16/25,
haces pasaje de potencia como raíz (suponemos que el ángulo α pertenece al primer cuadrante), y queda:
cosα = 4/5;
luego, reemplazas en la ecuación señalada (6), resuelves, y queda:
senα = 3/5.
Espero haberte ayudado. -
Hoola, como resuelvo este problema; con un alambre de 10 metros se quiere construir el borde de un rectangulo de area maxima, que dimensiones hay que dar al rectangulo?? y si una de las dimensiones tiene que tener entre 1,5 y 1,75 metros?? La primera pregunta si que puedo resolverla, la que no se como es la segunda cuestion. Gracias !!!
Antonio Silvio Palmitano
el 21/2/18Puedes llamar x a la base del rectángulo, e y a su altura.
Luego, tienes la relación entre ellas: 2x + 2y = 10,
divides por 2 en todos los términos, haces pasaje de término,y queda: y = 5 - x (1).
Luego, planteas el área del rectángulo, y queda:
A = x*y, sustituyes la expresión señalada (1), y queda la expresión de la función área del rectángulo en función de su base:
A(x) = x*(5 - x), distribuyes y ordenas términos, y queda:
A(x) = -x2 + 5x, resta y sumas 25/4 en la expresión de la función, y queda:
A(x) = -x2 + 5x - 25/4 + 25/4, extraes factor común -1 entre los tres primeros términos, y queda:
A(x) = -1*(x2 - 10x + 25/4) + 25/4, factorizas el trinomio cuadrado perfecto en el agrupamiento, y queda:
A(x) = -1*(x - 5/2)2 + 25/4, que es la expresión canónica de la función;
luego, planteas la expresión de la gráfica de la función, y queda:
y = -1*(x - 5/2)2 + 25/4,
que es la ecuación cartesiana canónica de una parábola cuyo vértice es el punto:
V(5/2,25/4) ≡ V( 2,5 ; 6,25 ),
y observa que la abscisa del vértice es el valor crítico, y que su ordenada es el área máxima que ya has calculado.
Luego, observa que la gráfica de la función es creciente en el intervalo en estudio: [ 1,5 ; 1,75 ],
por lo que tienes que:
el valor mínimo del área para este intervalo es:
A(1,5) = -1,52 + 5*1,5 = -2,25 + 7,5 = 5,25 m2;
el valor máximo del área para este intervalo es:
A(1,75) = -1,752 + 5*1,75 = -3,0625 + 8,75 = 5,6875 m2.
Espero haberte ayudado.
-
-
me pueden epxlicar lo siguiente por favor?
Si 0<θ<π2 y cosec(θ)=30 , entonces 30⋅(cos(θ))2+130=?
Antonius Benedictus
el 21/2/18Antonio Silvio Palmitano
el 21/2/18Tienes que el ángulo pertenece al primer cuadrante.
Tienes la ecuación
cosecθ = 30, sustituyes la expresión de la cosecante en función del seno, y queda:
1/senθ = 30, haces pasaje de divisor como factor y de factor como divisor, y queda:
1/30 = senθ (1);
luego, expresas al seno en función del coseno, y queda:
1/30 = √(1 - cos2θ), haces pasaje de raíz como potencia, y queda:
1/900 = 1 - cos2θ, haces pasajes de términos, y queda:
cos2θ = 899/900 (1), haces pasaje de potencia como raíz (observa que elegimos la raíz positiva), y queda:
cosθ = √(899/900) = √(899)/30
Luego, planteas la expresión de tu enunciado, y queda:
30*(cosθ)2 + 130 = reemplazas el valor señalado (1):
= 30*(899/900) + 130 = resuelves el primer término:
= 899/30 + 130 = extraes denominador común
= (899 + 3900)/30 = 4799/30.
Espero haberte ayudado.