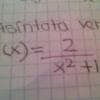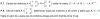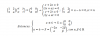-
Buenas noches únicos.... me prodrian ayudar con este ejercicio.. que pena molestarlos... gracias de antemano
Antonio Silvio Palmitano
el 21/2/18a)
Observa que en el intervalo: 0<t<6 tienes que la gráfica de la velocidad es constante, por lo tanto tienes para t = 3: a = 0;
observa que la gráfica de la velocidad es creciente en el intervalo [6,12], por lo tanto tienes para la aceleración en el intervalo (6,12):
a = (50-20)/(12-6) = 30/6 = 5 m/s2 (observa que es el valor de la pendiente del tramo recto correspondiente), por lo tanto tienes para t = 7: a = 5 m/s2;
observa que la gráfica de la velocidad es decreciente en el intervalo [12,15], por lo tanto tienes para la aceleración en el intervalo (12,15):
a = (0-50)/(15-12) = -50/3 m/s2 (observa que es el valor de la pendiente del tramo recto correspondiente), por lo tanto tienes para t = 14: a = -50/3 m/s2.
b)
Observa que la gráfica de la velocidad es recta en el segundo tramo, por lo que la pendiente es la misma en todos sus puntos (excepto en los extremos), por lo que la aceleración instantánea y la aceleración media coinciden en todos sus puntos, y lo mismo ocurre en el tercer tramo.
c)
Recuerda la propiedad del gráfico tiempo-velocidad de Movimiento Rectilíneo: "el área comprendida entre el eje Ot y la gráfica coincide con la distancia recorrida si la gráfica es positiva", por lo tanto tienes:
d1 = 6*20 = 120 (observa que para el primer tramo tienes un rectángulo, cuya base mide 6 y cuya altura mide 20),
d2 = (20+50)*6/2 = 70*3 = 210 (observa que para el segundo tramo tienes un trapecio cuya base menor mide 20, cuya base mayor mide 50 y cuya altura mide 6),
d3 = 3*50/2 = 3*25 = 75 (observa que para el tercer tramo tienes un triángulo rectángulo, cuya base mide 3 y cuya altura mide 50);
luego, tienes para la distancia total recorrida:
d = d1 + d2 + d3 = 120 + 210 + 75 = 405 m,
y como tienes que la posición inicial es x = 0, puedes concluir que la posición final del móvil es:
xf = xi + d = 0 + 405 = 405 m.
Espero haberte ayudado.
-
buen día,estoy estudiando el tema de integración por partes y el profesor me ha dado ese ejercicio junto con la respuesta con el fin de que me diera igual pero por mas que intento no me da igual, primero hago sustitución simple y luego la sustitución por partes pero no me da; gracias de antemano
Antonio Silvio Palmitano
el 21/2/18Has planteado bien la primera sustitución (s = t+1), y te ha quedado:
I = ∫ (s+1)*lns*ds = distribuyes = ∫ (s*lns + lns)*ds = ∫ s*lns*ds + ∫ lns*ds (*).
Luego, puedes plantear:
I1 = ∫ s*lns*ds,
aplicas el Método de Integración por partes ( u = lns, du = ds/s, dv = s*ds, v = s2/2), aplicas el método, y queda:
I1 = lns*s2/2 - ∫ (s2/2)*ds/s = (1/2)*s2*lns - (1/2)*∫ s*ds = (1/2)*s2*lns - (1/2)*s2/2 + C1 = (1/2)*s2*lns - (1/4)*s2 + C1 (1);
I2 = ∫ lns*ds,
aplicas el Método de Integración por partes ( u = lns, du = ds/s, dv = ds, v = s), aplicas el método, y queda:
I2 = lns*s - ∫ s*ds/s = s*lns - ∫ ds = s*lns - s + C2 (2);
luego, sustituyes las expresiones señaladas (1) (2) en la expresión señalada (*), reduces las constantes de integración, y queda:
I = (1/2)*s2*lns - (1/4)*s2 + s*lns - s + C;
que es la solución general de la integral de tu enunciado, en la que puedes ordenar términos y factorizar, para presentarla en otras formas equivalentes, por ejemplo:
I = (1/2)*s2*lns + s*lns - (1/4)*s2 - s + C = ( (1/2)*s2 + s )*lns - (1/4)*s2 - s + C,
y solo queda que en una u otra de las expresiones remarcadas sustituyas la expresión de la variable s en función de la variable t (s = t+1),
y observa que nuevamente tendrás la opción de desarrollar binomios elevados al cuadrado y distribuir.
Observa también que la estrategia que hemos empleado al comienzo de este desarrollo, en el que hemos presentado a la integral de tu enunciado como suma de dos integrales, nos ha permitido trabajar con expresiones más sencillas comparadas con las que tienes hechas en tu imagen.
Espero haberte ayudado.
-
jorge velazquez
el 21/2/18en principio tu funcion es continua en todos los reales y de manera sencilla para obtener las asintotas de una funcion p(x)/q(x) se cumple q(x)=0 y p(x) distinto de cero luego nota que x2+1=0 no tiene solucion en los reales esta claro pues el denominado nunca se hace cero luego la funcion no tiene asintotas verticales
-
Hola! Me podrían decir como se hace lo siguiente:
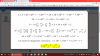
los lados de un triángulo a’b’c’ miden el doble que los de abc. Si la superficie del triángulo abc es 18 dm2. ¿Cual será la superficie del triángulo a’b’c’?
-
-
andres
el 20/2/18 -
andres
el 20/2/18Antonio Silvio Palmitano
el 22/2/18Si se trata de factorizar los polinomios cuadráticos, recuerda que la forma general es:
a*x2 + b*x + c = a*(x - x1)*(x - x2),
donde a es el coeficiente principal, y x1 y x2 son las raíces del polinomio, que puedes calcular con la Fórmula de Baskara.
1)
Igualas a cero la expresión del polinomio, y queda la ecuación
8*x2 - 53*x - 21 = 0,
que es una ecuación polinómica cuadrática cuyas raíces son: x1 = -3/8 y x2 = 7;
luego, tienes tu polinomio:
8*x2 - 53*x - 21 = 8*( x - (-3/8) )*(x - 7) = 8*(x + 3/8)*(x - 7).
2)
Igualas a cero la expresión del polinomio, y queda la ecuación
75*x2 + 120*x + 48 = 0, divides por 3 en todos los términos de la ecuación, y queda:
25*x2 + 40*x + 16 = 0,
que es una ecuación polinómica cuadrática cuyas raíces son: x1 = x2 = -4/5;
luego, tienes tu polinomio:
75*x2 + 120*x + 48 = 75*( x - (--4/5) )*( x - (-4/5) ) = 75*(x + 4/5)*(x + 4/5) = 75*(x + 4/5)2.
Espero haberte ayudado.