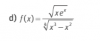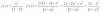-
César
el 12/2/18Antonio Silvio Palmitano
el 13/2/18Observa que tienes una división entre funciones, por lo que puedes plantear las expresiones del numerador y del denominador por separado, y también las expresiones de sus funciones derivadas, para luego aplicar la regla de derivación de la división entre dos funciones.
Para el numerador, tienes:
N = √(x*ex) = (x*ex)1/2 = x1/2*(ex)1/2= x1/2*ex/2,
y la expresión de su derivada primera queda:
N ' = (1/2)*x-1/2*ex/2 + x1/2*(1/2)*ex/2 = (1/2)*x-1/2*ex/2*(1 + x) = (1/2)*(1+x)*x-1/2*ex/2.
Para el denominador, tienes:
D = 4√(x3 - x2) = (x3 - x2)1/4 = ( x2*(x - 1) )1/4 = (x2)1/4*(x - 1)1/4= x1/2*(x - 1)1/4.
y la expresión de su derivada primera queda (observa que debes aplicar la regla de derivación de una multiplicación de funciones):
D ' = (1/2)*x-1/2*(x - 1)1/4 + x1/2*(1/4)*(x - 1)-3/4 = (1/4)*x-1/2*(x - 1)-3/4*(2*(x - 1) + x) = (1/4)*x-1/2*(x - 1)-3/4*(3x - 1) = (1/4)*(3x - 1)*x-1/2*(x - 1)-3/4.
Luego, queda que apliques la regla de derivación de una división de funciones, ya que tienes:
f(x) = N/D,
por lo que la expresión de su función derivada queda:
f ' (x) = [( N ' )*D - N*( D ' )] / D2,
y solo queda que sustituyas las expresiones remarcadas del numerador, del denominador, y de sus derivadas, para luego reducir todo a su mínima expresión (te dejo la tarea).
Espero haberte ayudado.
-
-
Hola, no sé por donde empezar con esta integral:
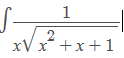
¿Podéis echarme una mano? Gracias.
Antonius Benedictus
el 15/2/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Buenas, la solución de la derivada de x^2 / 1-x es -x^2 + 2x / (x-1)^2 pero a mi en el denominador me da (1-x)^2 . Me ayudais?? No se en que es lo que fallo. Graciasss
Antonio Silvio Palmitano
el 12/2/18Además, observa que los denominadores a los que te refieres son equivalentes, pues tienes:
(x - 1)2 = (1 - x)2;
luego, desarrollas los binomios elevados al cuadrado para verificar, y queda:
x2 - 2x + 1 = 1 - 2x + x2,
que es una identidad verdadera entre expresiones polinómicas.
Espero haberte ayudado.
-
Buenas, pueden ayudarme con este ejercicio: Aplica el teorema del valor medio a la función f(x) = -x^2 + 2x - 8 en el intervalor [-3,3] e interpretalo geometricamente. Graciaaas