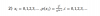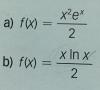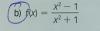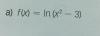-
Ángel
el 13/2/18P2 es el espacio vectorial de los polinomios de grado menor o igual que dos.
P2 tiene dimensión 3 y para ello hay que comprobar que los tres términos sean independientes.
P2 tiene como base canónica B={1,x,x2}
--------------------------------
a)
p1 tiene 3 términos independientes, SÍ genera P2
p2 tiene sólo 2 términos y aunque sean independientes entre ellos, NO genera P2
b)
p1 tiene 3 términos independientes, SÍ genera P2
p2 y p3 tienen sólo 1 término, NO generan P2
-
Mauro
el 12/2/18Antonio Silvio Palmitano
el 12/2/18a)
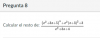
Observa que el dominio de la función es R.
Luego, planteas la expresión de la función derivada primera, y queda:
f ' (x) = (2x*ex + x2*ex)/2 = x*ex*(2 + x)/2;
luego, planteas la condición de punto crítico (posible máximo o posible mínimo), y queda:
f ' (x) = 0, sustituyes la expresión de la función derivada primera en el primer miembro, y queda:
x*ex*(2 + x)/2 = 0, haces pasaje de divisor como factor, y queda:
x*ex*(2 + x) = 0, haces pasaje del factor exponencial (recuerda que toma valores estrictamente positivos) como divisor, y queda:
x*(2 + x) = 0;
luego, por anulación de un producto, tienes dos soluciones, que son los puntos críticos:
x1 = -2, y x2 =0;
luego, divides al dominio en intervalos, eliges un representante en cada uno de ellos y evalúas el signo de la expresión de la función derivada primera ellos, a fin de determinar el crecimiento o decrecimiento de la gráfica de la función, y tienes:
(-∞,-2), representado por x = -3, y el valor de la función derivada primera para él queda: f ' (-3) = 3*e-3/2 > 0, por lo que tienes que la gráfica de la función es creciente;
(-2,0), representado por x = -1, y el valor de la función derivad primera para él queda: f ' (-1) = -e-1/2 < 0, por lo que tienes que la gráfica de la función es decreciente;
(0,+∞), representado por x = 1, y el valor de la función derivad primera para él queda: f ' (-1) = 3e/2 > 0, por lo que tienes que la gráfica de la función es creciente;
por lo que puedes concluir que la gráfica de la función alcanza un máximo en x1 = -2 y un mínimo en x2 = 0.
b)
Observa que el dominio de la función es D = (0,+∞).
Luego, planteas la expresión de la función derivada primera, y queda:
f ' (x) =( 1*lnx + x*(1/x) )/2 = (lnx + 1)/2;
luego, planteas la condición de punto crítico (posible máximo o posible mínimo), y queda:
f ' (x) = 0, sustituyes la expresión de la función derivada primera en el primer miembro, y queda:
(lnx + 1)/2 = 0, haces pasaje de divisor como factor, y queda:
lnx + 1 = 0, haces pasaje de término, y queda:
lnx = -1, compones en ambos miembros con la función inversa del logaritmo natural, y queda;
x1 = e-1 ≅ 0,3679;
luego, divides al dominio en intervalos, eliges un representante en cada uno de ellos y evalúas el signo de la expresión de la función derivada primera ellos, a fin de determinar el crecimiento o decrecimiento de la gráfica de la función, y tienes:
(0,e-1), representado por x = e-2 ≅ 0,1353, y el valor de la función derivada primera para él queda: f ' (e-2) = -1/2 < 0, por lo que tienes que la gráfica de la función es decreciente;
(e-1,+∞), representado por x = 1, y el valor de la función derivad primera para él queda: f ' (1) = 1/2 > 0, por lo que tienes que la gráfica de la función es creciente;
por lo que puedes concluir que la gráfica de la función alcanza un mínimo en x1 = e-1.
Espero haberte ayudado.
-
Mauro
el 12/2/18Antonio Silvio Palmitano
el 13/2/18Observa que el dominio de la función es R.
Luego planteas la expresión de la función derivada primera, y queda:
f ' (x) = (2x*(x2 + 1) - (x2 - 1)*2x)/(x2 + 1)2 = 4x/(x2 + 1)2;
luego, planteas la condición de punto crítico (posible máximo o posible mínimo):
f ' (x) = 0, sustituyes la expresión de la función derivada primera, y queda:
4x/(x2 + 1)2 = 0, haces pasaje de divisor (observa que toma valores estrictamente positivos) como factor, y queda:
4x = 0, haces pasaje de factor como divisor, y queda:
x1 = 0;
luego, divides al dominio en intervalos, eliges un representante en cada uno de ellos y evalúas el signo de la expresión de la función derivada primera ellos, a fin de determinar el crecimiento o decrecimiento de la gráfica de la función, y tienes:
(-∞,0), representado por x = -1, y el valor de la función derivada primera para él queda: f ' (-1) = -1 < 0, por lo que tienes que la gráfica de la función es decreciente;
(0,+∞), representado por x = 1, y el valor de la función derivada primera para él queda: f ' (1) = 1 > 0, por lo que tienes que la gráfica de la función es creciente;
luego, puedes concluir que la gráfica de la función es monótona decreciente en el primer intervalo, que es monótona creciente en el segundo intervalo, y que alcanza un mínimo en x1 = 0.
Espero haberte ayudado.
-
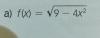 Como encuentro los puntos de corte? Esque me da y= +3 y= -3 pero sé que esta mal y no da eso y la x no se como calcularla
Como encuentro los puntos de corte? Esque me da y= +3 y= -3 pero sé que esta mal y no da eso y la x no se como calcularlaÁngel
el 12/2/18Mauro
el 12/2/18Antonio Silvio Palmitano
el 13/2/18Observa que el argumento de la raíz cuadrada debe cumplir la condición:
9 - 4x2 ≥ 0, haces pasaje de término, y queda:
-4x2 ≥ -9, haces pasaje de factor como divisor (observa que cambia la desigualdad), y queda:
x2 ≤ 9/4, haces pasaje de potencia (observa que el exponente es par) como raíz, y queda:
|x| ≤ 3/2, desarrollas la inecuación como doble inecuación, y queda:
-3/2 ≤ x ≤ 3/2,
por lo que tienes que el dominio de la función es el intervalo cerrado: D = [ -3/2 , 3/2 ].
Luego, planteas la condición de intersección con el eje coordenado OX, y queda:
f(x) = 0, sustituyes la expresión de la función y queda:
√(9 - 4x2) = 0, haces pasaje de raíz como potencia, y queda:
9 - 4x2 = 0, haces pasaje de término, y queda:
-4x2 = -9, haces pasaje de factor como divisor, y queda:
x2 = 9/4, haces pasaje de potencia (observa que el exponente es par) como raíz, y queda:
|x| = 3/2;
luego, de acuerdo con la definición de valor absoluto, tienes dos opciones:
x1 = -3/2, que pertenece al dominio de la función, por lo que tienes el punto de corte: A1(-3/2,0);
x2 = 3/2, que pertenece al dominio de la función, por lo que tienes el punto de corte: A2(3/2,0).
Luego, observa que x = 0 pertenece al dominio de la función, por lo que planteas la condición de intersección con el eje coordenado OY, y queda:
f(0) = √( 9 - 4*02) = √(9) = 3, por lo que tienes que la gráfica de la función corta al eje OY en y = 3, y tienes el punto de corte: B(0,3).
Espero haberte ayudado.
-
Ángel
el 12/2/18¿Te refieres a porqué no existe la función desde -√3 hasta √3 ?
Es porque si das valores de x entre esos números, por ejemplo -1,0, 1 obtienes un ln negativo y no existe en los reales.
¿Te refieres a porqué aunque x tienda a ±infinito sube tan despacio el valor de y?
Ten en cuenta que, cuando x=1000 la f(x)=y= ln(10002-3) = 13,81
Antonio Silvio Palmitano
el 13/2/18Vamos con una orientación.
Observa que el argumento del logaritmo debe cumplir al condición:
x2 - 3 > 0, haces pasaje de término, y queda:
x2 > 3, haces pasaje de potencia (observa que el exponente es par) como raíz, y queda:
|x| > √(3), despliegas el valor absoluto, y queda:
x < -√(3) o x > √(3), y tienes que el dominio de la función queda expresado: D = ( -∞ , -√(3) ) u ( √(3) , +∞ ).
Luego, planteas:
f(-x) = ln( (-x)2 - 3 ) = ln(x2 - 3) = f(x),
y tienes que la función es par, por lo que la gráfica de la función es simétrica con respecto al eje coordenado OY.
Luego, planteas la condición de intersección con el eje coordenado OX:
f(x) = 0, sustituyes la expresión de la función en el primer miembro, y queda:
ln(x2 - 3) = 0, compones en ambos miembros con la función inversa del logaritmo natural, y queda:
x2 - 3 = 1, haces pasaje de término, y queda:
x2 = 4, haces pasaje de potencia (observa que el exponente es par) como raíz, y queda:
|x| = 2, por lo que tienes dos soluciones:
x1 = -2, que corresponde al punto: A1(-2,0),
x2 = 2, que corresponde al punto: A2(2,0).
Luego, observa que x = 0 no pertenece al dominio de la función, por lo que su gráfica no corta al eje coordenado OY.
Luego, planteas los límites (te dejo la tarea), y tienes:
Lím(x→-∞) f(x) = +∞,
Lím( x→-√(3) ) f(x) = -∞,
Lím( x→√(3) ) f(x) = -∞,
Lím(x→+∞) f(x) = +∞.
Luego, planteas la expresión de la función derivada primera, y queda:
f ' (x) = 2x/(x2 - 3), y observa que el denominador toma valores positivos en todo el dominio de la función, por lo que tienes:
f ' (x) < 0 en el intervalo ( -∞ , -√(3) ), por lo que la gráfica de la función es decreciente en este intervalo;
f ' (x) > 0 en el intervalo ( √(3) , +∞ ), por lo que la gráfica de la función es creciente en este intervalo.
Luego, planteas la expresión de la función derivada segunda, y queda:
f ' ' (x) = (2*(x2 - 3) - 2x*2x)/(x2 - 3)2 = (-2x2 - 6)/(x2 - 3)2 = -2*(x2 + 3)/(x2 - 3)2,
y observa que esta expresión toma valores estrictamente negativos (observa que su denominador toma valores estrictamente positivos, y que su denominador toma valores estrictamente negativos), por lo que tienes que la gráfica de la función es cóncava hacia abajo en ambos intervalos que conforman el dominio de la función.
Espero haberte ayudado.
-
Hola, tengo una duda con este ejercicio de probabilidad,en cuanto al ejemplo de las monedas, ¿qué significa p(A∩B)? ¿la probabilidad de obtener una cara habiendo obtenido una cruz?
Gracias
Ángel
el 13/2/18La regla de Laplace en estos casos dice que la probabilidad de un suceso son los casos favorables entre los casos posibles
Tienes que la probabilidad tanto de sacar cara P(A), como de sacar cruz P(B) es de 1 entre 2 P(A)=P(B)= 1/2
P(A υ B) significa la probabilidad de obtener una cara o una cruz, y coincide precisamente con P(A) y P(B), porque si sacamos una cara no sacamos cruz y viceversa(no son independientes)
Antonio Silvio Palmitano
el 13/2/18Vamos con una orientación.
Tienes el experimento aleatorio: "se lanza una moneda equilibrada dos veces", y observa que su espacio muestral (conjunto de resultados posibles) queda expresado (indicamos cara con C, y cruz con S):
S = { CC , CS , SC , SS }.
Luego, tienes los sucesos:
A: "se obtiene una cara", que expresado como subconjunto del espacio muestral queda: A = { CS , SC }, y su probabilidad queda: p(A) = 2/4 = 1/2;
B: "se obtiene una cruz", que expresado como subconjunto del espacio muestral queda: B = { CS , SC }, y su probabilidad queda: p(B) = 2/4 = 1/2;
luego, tienes el suceso: A intersección B, que corresponde a la ocurrencia de los dos sucesos al mismo tiempo:
A ∩ B: "se obtiene una cara y una cruz", que expresado como subconjunto del espacio muestral queda: A ∩ B = { CS , SC },
y su probabilidad queda: p(A ∩ B) = 2/4 = 1/2.
Observa que los tres sucesos son iguales, por lo que la ocurrencia de A obliga la ocurrencia de B (o la ocurrencia de B obliga la ocurrencia de A), y lo mismo acontece con la no ocurrencia de uno de los sucesos que obliga la no ocurrencia del otro, por lo que tienes que los sucesos no son independientes, y tienes:
p(A)*p(B) = (1/2)*(1/2) = 1/4, y p(A ∩ B) = 1/2.
Luego, recuerda la definición de la probabilidad condicional:
p(A|B) = p(A ∩ B)/P(B) (1).
Luego, recuerda la definición de independencia entre sucesos:
p(A|B) = p(A);
luego, sustituyes la expresión señalada (1) en e primer miembro, y queda:
p(A ∩ B)/P(B) = p(A), haces pasaje de divisor como factor, y queda:
p(A ∩ B) = p(A)*p(B), que es la relación entre probabilidades de dos sucesos independientes, que no se cumple para los sucesos de tu enunciado.
Espero haberte ayudado.
-
Mauro
el 12/2/18Antonio Silvio Palmitano
el 13/2/18Puedes comenzar por tratar a cada término por separado, hasta expresarlos a todos con logaritmos con la misma base, en este ejercicio en base tres:
Primer término:
a = log√(3)(x), compones en ambos miembros de la ecuación con la función inversa del logaritmo en base √(3), y queda:
( √(3) )a = x, expresas a la raíz como una potencia con exponente fraccionario, y queda:
(31/2)a = x, aplicas la propiedad de la potencia cuya base es otra potencia, y queda:
3(1/2)*a = x, compones en ambos miembros de la ecuación con la función logaritmo en base 3, y queda:
log3( (31/2)a ) = log3(x), aplicas la propiedad de la potencia cuya base es otra potencia en el argumento del logaritmo en el primer miembro, y queda:
log3(3(1/2)*a) = log3(x), aplicas la propiedad del logaritmo de una potencia en el primer miembro, y queda:
(1/2)*a*log3(3) = log3(x), resuelves el logaritmo en el primer miembro (observa que es igual a 1), multiplicas por 2 en ambos miembros, y queda:
a = 2*log3(x) (1);
Segundo término:
b = 2*log3(x) (2);
Tercer término:
c = (1/2)*log1/3(x-1), aplicas la propiedad del logaritmo de una potencia, y queda:
c = log1/3( (x-1)1/2 ), aplicas la propiedad de la potencia cuya base es otra potencia en el argumento del logaritmo, y queda:
c = log1/3(x-1/2), compones en ambos miembros con la función inversa del logaritmo en base 1/3, y queda:
(1/3)c = x-1/2, expresas a la base de la potencia del primer miembro como potencia, y queda:
(3-1)c = x-1/2, aplicas la propiedad de la potencia cuya base es otra potencia en el primer miembro, y queda:
3-c = x-1/2, compones en ambos miembros con la función logaritmo en base 3, y queda:
log3(3-c) = log3(x-1/2), aplicas la propiedad del logaritmo de una potencia en ambos miembros, y queda:
-c*log3(3) = -(1/2)*log3(x), resuelves el logaritmo en el primer miembro (observa que es igual a 1), multiplicas por -1 en ambos miembros, y queda:
c = (1/2)*log3(x) (3).
Luego, tienes la ecuación de tu enunciado:
log√(3)(x) + 2*log3(x) - (1/2)*log1/3(x-1) = 1;
sustituyes las expresiones señaladas (1) (2) (3), y queda:
2*log3(x) + 2*log3(x) - (1/2)*log3(x) = 1;
reduces términos semejantes, y queda:
(7/2)*log3(x) = 1;
multiplicas en ambos miembros por 2/7, y queda:
log3(x) = 2/7;
compones en ambos miembros con la función inversa del logaritmo en base 3, y queda:
x = 32/7;
expresas el segundo miembro como una raíz cuya base es una potencia, y queda:
x = 7√(32).
Espero haberte ayudado.