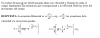Establece un sistema de referencia con eje OX paralelo al suelo, que pase por el punto B, con sentido positivo acorde al desplazamiento del móvil, y con eje OY vertical, con sentido positivo hacia arriba.

Consideramos que el módulo de la aceleración gravitatoria terrestre es: g = 10 m/s².

Luego, planteas las expresiones de las energías potencial gravitatoria, cinética de traslación y mecánica del móvil en el punto A, y queda:

EP_A = M*g*y_A,

EC_A = (1/2)*M*v_A²,

EM_A = EP_A  + EC_A = M*g*y_A + (1/2)*M*v_A² (1).

Luego, planteas las expresiones de las energías potencial gravitatoria, cinética de traslación y mecánica del móvil en el punto B, y queda:

EP_B = M*g*y_B,

EC_B = (1/2)*M*v_B²,

EM_B = EP_B  + EC_B = M*g*y_B + (1/2)*M*v_B² (2).

Luego, planteas las expresiones de las energías potencial gravitatoria, cinética de traslación y mecánica del móvil en el punto C, y queda:

EP_C = M*g*y_C,

EC_C = (1/2)*M*v_C²,

EM_C = EP_C  + EC_C = M*g*y_C + (1/2)*M*v_C² (3).

Luego, si se desprecian las pérdidas por rozamientos, puedes plantear que la energía se conserva, y tienes la ecuación:

EM_C = EM_A, sustituyes las expresiones señaladas (3) (1), y queda:

M*g*y_C + (1/2)*M*v_C² = M*g*y_A + (1/2)*M*v_A², multiplicas en todos los términos por 2/M, y queda:

2*g*y_C + v_C² = 2*g*y_A + v_A², restas x en ambos miembros, y queda:

v_C² = 2*g*y_A + v_A² - 2*g*y_C,

extraes factores comunes (-2*g) entre el primer y el último término del segundo miembro, y queda:

v_C² = -2*g*(-y_A + y_C) + v_A²,

aquí reemplazas datos que tienes en la imagen (y_A = 5 m, y_C = 8 m, v_A = 5 m/s), y queda:

v_C² = -2*10*(-5 + 8) + 5², resuelves términos, y queda:

v_C² = -60 + 25, resuelves y queda:

v_C² = -25 m²/s²,

que es un resultado absurdo (recuerda que las expresiones cuadráticas toman valores mayores o iguales que cero),

por lo que puedes concluir que el móvil no alcanzará el punto C con las condiciones que tienes en tu enunciado.

Luego, sería muy conveniente que consultes con tus docentes, por las dudas se trate de un error de impresión en dicho enunciado.

Espero haberte ayudado.

Buenas, te recomendaría los siguientes libros:

- Física (M. Alonso y E. J. Finn)

- Física universitaria (Sears, Zemansky, Young y Freedman)

- Física (R. A. Serway)

- Física (P. A. Tipler y G. Mosca)

Saludos y a disfrutar de la física!

Muchas gracias 

Claro que la disfrutare ^^

Tienes la longitud estimada de la arista del cubo en estudio:

L₀ = 25,7 cm = 0,257 m.

Tienes el valor del error máximo que puede cometerse al medir la arista del cubo en estudio:

ΔL₀ = 0,1 cm = 0,001 m.

Recuerda la expresión del volumen del cubo en función de la longitud de su arista:

V(L) = L³ (1), derivas, y queda:

dV/dL = 3*L², separas variables, y queda:

dV = 3*L²*dL (2).

Luego, evalúas la expresión señalada (1) para este valor, y queda:

V₀ = 0,257³ = 0,016974593 m³ (3),

que es el volumen estimado del cubo.

Luego, a partir de la expresión señalada (2), planteas la expresión del error, y queda:

ΔV₀ = 3*L₀²*ΔL, reemplazas valores, y queda:

ΔV₀ = 3*0,257²*0,001, resuelves, y queda:

ΔV₀ = 0,000198147 m³ (4),

que es el error máximo que se puede cometer al medir el volumen del cubo en estudio.

Luego, planteas la expresión del volumen del cubo en estudio, y queda:

V = V₀ + ΔV, reemplazas los valores señalados (3) (4), y queda:

V = (0,016974593 ± 0,000198147) m³.

Espero haberte ayudado.

Observa que la intensidad de corriente que rodea una espira es: I;

luego, planteas la Ley de Ampere, y tienes la ecuación:

B*L = μ₀*I, aquí divides por L en ambos miembros, y queda:

B = μ₀*I/L,

que es la expresión del módulo del campo magnético que atraviesa una espira;

luego, planteas la expresión del flujo magnético que atraviesa una espira, y queda:

Φ = B*A, sustituyes expresiones, y queda:

Φ = (μ₀*I/L)*π*R²;

luego, planteas la expresión del flujo total que atraviesa todas las espiras, y queda:

Φ_T = N*Φ, sustituyes la expresión anterior, y queda:

Φ_T = N*(μ₀*I/L)*π*R²,

que es la expresión del flujo total que atraviesa todas las espiras del inductor.

Espero haberte ayudado.

Si me sirvió de mucho. Pero mi duda continúa.

Si calculo la fuerza electromotriz del solenoide como la derivada del flujo respecto de t con signo menos me queda una expresión con N.

Si ahora calculo la inductancia L me queda una expresión con N al cuadrado. Y si calculo la fem como L por la derivada de la corriente respecto del tiempo me queda la misma expresión pero con N al cuadrado.

No se donde está el error y cuál de las dos expresiones de la fem, si con N o con N al cuadrado es la correcta.

Te agradezco tu respuesta y me será muy útil ya que pronto tengo que recuperar mi examen de fisica II.

Muchas gracias.

Comienza por trazar una recta paralela al eje OX que pasa por el punto en estudio (P), y observa que es perpendicular a los cables.

Luego, aplicas la Ley de Ampère, y tienes las expresiones de los módulos de los campos magnéticos en el punto en estudio:

B₁ = μ₀*I₁/(2π*r₁) (observa que r₁ es igual a 40 cm = 0,4 m),

B₂ = μ₀*I₂/(2π*r₂) (observa que r₂ es igual a 20 cm = 0,2 m).

Luego, considera elementos de corriente ubicados en las intersecciones de los cables con la recta trazada, y tienes que sus expresiones vectoriales son (observa que las corrientes tienen sentidos opuestos al eje OY):

(-I₁*dL₁)j y (-I₂*dL₁)j.

Luego, planteas las expresiones de los vectores posiciones del punto P con respecto a los elementos de corriente, y queda:

(+0,4)i y (+0,2)i.

Luego, planteas la Ley de Lorentz (dB = (I*dL)xB), y los diferenciales de los campos magnéticos en el punto P quedan:
dB₁ = (-I₁*dL₁)j x (+0,4)i  = (-0,4*I₁*dL₁)*(j x i) = (-0,4*I₁*dL₁)*(-k) = (+0,4*I₁*dL₁)*k,

dB₂ = (-I₂*dL₂)j x (+0,2)i  = (-0,2*I₂*dL₂)*(j x i) = (-0,2*I₂*dL₂)*(-k) = (+0,2*I₂*dL₂)*k,

y puedes observar que las dos expresiones vectoriales tienen el sentido positivo del eje OZ.

a)

Planteas la expresión del módulos del campo magnético resultante en el punto P, y queda:

B = B₁ + B₂, sustituyes expresiones, y queda:

B = μ₀*I₁/(2π*r₁) + μ₀*I₂/(2π*r₂), extraes factores y divisores comunes, y queda:

B = ( μ₀/(2π) )*( I₁/r₁ + I₂/r₂ );

y la expresión vectorial del campo resultante queda:

B = ( μ₀/(2π) )*( I₁/r₁ + I₂/r₂ )*k,

y solo queda que reemplaces valores y hagas el cálculo.

b)

Tienes el valor de la carga (indicamos con e el valor de la carga elemental: e = 1,6*10^-19 C):

q = -e.

Tienes la expresión vectorial de la velocidad de la carga:

v = -10⁶*i.

Luego, planteas la Ley de Lorentz ( F = q*(v x B) ), sustituyes expresiones, y queda:

F = (-e)*( (-10^-6*i) x (B*k) ) = (+10^-6*e*B)*( i x k ) = (+10^-6*e*B)*( -j ) = (-10^-6*e*B)*j,

observa que la fuerza ejercida sobre la carga tiene la dirección del eje OY con su sentido negativo,

y que sol queda que reemplaces valores y hagas el cálculo.

Espero haberte ayudado.

a)

Tienes que el saltador es capaz de saltar 2 m en la Tierra, y como esta altura es muy pequeña, puedes plantear la ecuación de Energía usual sin consideraciones de gravitación (consideramos un eje de posiciones OY vertical con sentido positivo hacia arriba, con origen de coordenadas al nivel del suelo):

EP_i + EC_i = EP_f + EC_f, sustituyes expresiones, y queda:

M*g*h_i + (1/2)*M*v_i² = M*g*h_f + (1/2)*M*v_f², multiplicas por 2 y divides por M en todos los términos, y queda:

2*g*h_i + v_i² = 2*g*h_f + v_f², reemplazas datos (v_i = v_T, h_i = 0, v_f = 0, h_f = 2 m, g = 9,8 m/s²), y queda:

2*9,8*0 + v_T² = 2*9,8*2 + 0², resuelves términos, cancelas términos nulos, y queda:

v_T² = 39,2, extraes raíz cuadrada positiva en ambos miembros, y queda:

v_T ≅  6,261 m/s, que es la velocidad inicial del saltador en la Tierra.

Luego, tienes que la velocidad cuyo módulo hemos remarcado es la velocidad de escape del asteroide Rocón, por lo que planteas la ecuación de energía, y queda:

EP₁ + EC₁ = EP₂ + EC₂, planteas la condición de escape (EP₂ = 0 y EC₂ = 0), y queda:

EP₁ + EC₁ = 0,

sustituyes expresiones (observa que aquí si hacemos consideraciones de gravitación, y que el valor remarcado corresponde a la velocidad de escape del asteroide Rocón), y queda:

-G*M_R*M/R_R + (1/2)*M*v_T² = 0, multiplicas por 2/M en todos los términos, y queda:

-2*G*M_R/R_R + v_T² = 0, sumas u en ambos miembros, y queda:

v_T² = 2*G*M_R/R_R, expresas a la masa de Rocón en función de densidad y de su radio, y queda:

v_T² = 2*G*(4/3)π*ρ_T*R_R³/R_R, resuelves el coeficiente, simplificas, y queda:

v_T² = (8/3)π*G*ρ_T*R_R², aquí reemplazas datos (observa que empleamos unidades internacionales), y queda:

6,261² ≅ (8/3)π*6,67*10^-11*5,5*10³*R_R², resuelves operaciones numéricas, y queda:

39,200 ≅ 307,332*10^-8*R_R², divides por 307,332 y multiplicas por 10⁸ en ambos miembros, y queda:

0,128*10⁸≅ R_R², extraes raíz cuadrada positiva en ambos miembros, y queda:

0,357*10⁴ m ≅ R_R, resuelves el primer miembro, y queda:

3570 m ≅ R_R (observa que la diferencia de valores se debe a las aproximaciones).

Haz el intento de resolver los demás apartados, y si te resulta necesario no dudes en volver a consultar.

Espero haberte ayudado.

Considera un sistema de referencia cartesiano usual, con eje OX horizontal con sentido positivo hacia la derecha acorde al sentido de la fuerza aplicada (F, que consideramos tiene dirección horizontal), y con eje OY vertical con sentido positivo hacia arriba.

Luego, observa que sobre el cuerpo actúan cuatro fuerzas, de las que indicamos sus módulos, direcciones y sentidos:

Peso: P = M*g = 10*9,8 = 98 N, vertical, hacia abajo;

Acción normal del plano: N, vertical, hacia arriba;

Rozamiento del plano: fr = μ*N = 0,35*N, horizontal, hacia la izquierda;

Fuerza aplicada: F, horizontal, hacia la derecha.

Luego, planteas las expresiones de las componentes de la fuerza resultante (R), y queda:

R_x = F - fr,

R_y = N - P; 

luego, reemplazas el valor del módulo del Peso, sustituyes la expresión del módulo de la fuera de rozamiento, y queda (observa que las fuerzas verticales se equilibran, ya que el cuerpo se desplaza con dirección horizontal):

a)

R_x = F - 0,35*N,

N - 98 = 0, y de aquí despejas: N = 98 N (módulo de la acción normal del plano);

luego, reemplazas este último valor en la primera ecuación, resuelves el último término, y queda:

R_x = F - 34,3, que es la expresión de la componente horizontal de la fuerza resultante,

y observa también que el módulo de la fuerza de rozamiento es: fr = 34,3 N como bien has consignado.

y como puedes apreciar, para poner el cuerpo en movimiento se necesita que el módulo de la fuerza aplicada (F) sea mayor o igual que 34,3 N, por lo que tienes que la fuerza cuyo módulo es: F = 20 N no provoca desplazamiento, por lo que el cuerpo permanece en reposo y la componente horizontal de la fuerza resultante es igual a cero, y como la componente vertical también lo es, entonces tienes que la fuerza resultante es nula.

b)

Ahora sí, como tienes una fuerza cuyo módulo es mayor que 34,3 N, entonces tienes (observa que consideramos que el rozamiento en este caso es dinámico):

R_x = 50 - 34,3, resuelves, y queda:

R_x = 15,7 N, que es el módulo de la componente horizontal de la fuerza resultante;

luego, aplicas la Segunda Ley de Newton (recuerda que la componente vertical de la fuerza resultante es igual a cero), y queda:

R_x = M*a_x, y de aquí despejas:

a_x = R_x/M, que es la expresión de la componente horizontal de la aceleración;

luego, reemplazas valores, resuelves, y queda:

a_x = 1,57 m/s², que es el valor de la componente horizontal de la aceleración,

y como la componente vertical de la fuerza resultante es igual a cero, entonces tienes: a_y = 0.

Espero haberte ayudado.

Tu planteamiento es muy lógico. Lo único no me cuadra la fuerza resultante. Entiendo lo que dices de que al ser la fuerza de rozamiento mayor no hay movimiento, pero eso es evidente. Si tú ejerces una fuerza de 30 a un lado y 20 a otro. Va a ir al sentido de la de 30. Yo pienso que aquí aunque no se mueva por ser rozamiento, la fuerza resultante = -14,3N, te indica la fuerza que está actuando en el otro sentido(y que hay que vencer para moverlo). Porque si ponemos la fuerza resultante es nula. FR = F - Fr     0= 20-34,3   Esta operación, matemáticamente, carecería de sentido, ¿no?

Respecto al apartado a, es una duda que me estaba planteando. Veo dos posibles casos:

1) El cuerpo está inicialmente en reposo:

Para acelerarlo se necesita aplicar una fuerza mayor a la fuerza de rozamiento estático, y también dinámico. Como no es el caso, se podría concluir que no acelera y que la fuerza de rozamiento debe ser del tipo estático. La resultante debe ser cero y por tanto la fuerza de rozamiento es igual a -20N.

2) El cuerpo tiene inicialmente una velocidad:

En este caso no habría ningún problema en que la fuerza de rozamiento sea mayor que la fuerza aplicada y que su resultante sea -14.3 N. Simplemente implica que el cuerpo desacelera, y eventualmente terminaría en reposo.

Espero haber ayudado en algo.

Establece un sistema de referencia con eje de posiciones (alturas) OX vertical con sentido positivo hacia arriba, y observa que en este sistema tienes:

g = -9,8 m/s² (aceleración gravitatoria terrestre),

v < 0 (la velocidad tiene sentido hacia abajo);

Luego, planteas la expresión del peso del cuerpo y de la fuerza de resistencia viscosa, y queda:

P = M*g (observa que esta expresión es negativa),

R = -k*v (observa que esta expresión es positiva).

Luego, aplicas la Segunda Ley de Newton, y tiene la ecuación:

P + R = M*a, sustituyes las expresiones de las fuerzas, y queda:

M*g - k*v = M*a (1).

a)

Expresas a la velocidad como la derivada de la posición con respecto al tiempo, expresas a la aceleración como la derivada segunda de la posición con respecto al tiempo, sustituyes expresiones en la ecuación señalada (1), y queda:

M*g - k*(dx/dt) = M*(d²x/dt²),

que es la ecuación diferencial que tienes en tu solucionario.

b)

Expresas a la aceleración como la derivada de la velocidad con respecto al tiempo, sustituyes en la ecuación señalada (1), y queda:

M*g - k*v = M*(dv/dt), separas variables, y queda:

dt = M*dv/(M*g - k*v), divides por M y multiplicas por -k en ambos miembros, y queda:

-(k/M)*dt = -k*dv/(M*g - k*v), integras en ambos miembros, y queda:

-(k/M)*(t + C) = ln(|M*g - k*v|), compones en ambos miembros con la función inversa del logaritmo natural, y queda:

e^{-(k/M)*(t + C)} = M*g - k*v, sumas k*v y restas u en ambos miembros, y queda:

k*v = M*g - e^{-(k/M)*(t + C)}, multiplicas en ambos miembros por 1/k, y queda:

v = (1/k)*( M*g - e^{-(k/M)*(t + C)} ),

que es la expresión de la velocidad como función del tiempo que tienes en tu enunciado.

c)

Expresas a la velocidad como la derivada de la posición con respecto al tiempo, sustituyes en la última ecuación remarcada, y queda

dx/dt = (1/k)*( M*g - e^{-(k/M)*(t + C)} ), separas variables, y queda:

dx = (1/k)*( M*g - e^{-(k/M)*(t + C)} )*dt, distribuyes el segundo miembro, y queda:

dx = (M/k)*g*dt - (1/k)*e^{-(k/M)*(t + C)}*dt, integras en ambos miembros, y queda

x = (M/k)*g*t + (M/k²)*e^{-(k/M)*(t + C)} + D, extraes factor común M/k entre los dos primeros términos, y queda:

x = (M/k)*( g*t + (1/k)*e^{-(k/M)*(t + C)} ) + D,

que es la expresión de la posición como función del tiempo que tienes en tu enunciado.

Espero haberte ayudado.

Tienes los datos:

R = 384400 Km = 384400000 m (radio orbital de la Luna).

T = 27,3 días = 27,3*24*3600 = 2358720 s (periodo orbital de la Luna.

Luego, planteas la expresión del módulo de la velocidad tangencial de la Luna como la división de la longitud de su órbita entre el periodo orbital, y queda:

v = 2π*R/T, reemplazas valores, y queda:

v = 2π*384400000/2358720, resuelves, y queda:

v ≅ 1023,969 m/s.

Luego, planteas la expresión del módulo de la aceleración centrípeta en función del módulo de la velocidad tangencial y del radio orbital, y queda:

a_cp= v²/R, reemplazas valores, y queda:

a_cp ≅ 1023,969²/384400000, resuelves, y queda:

a_cp ≅ 0,003 m/s² (1).

Luego, planteas la expresión del módulo de la fuerza centrípeta que la Tierra ejerce sobre la Luna, en función de la masa lunar y del módulo de la aceleración centrípeta, y queda:

F_cp = M*a_cp, reemplazas valores, y queda:

F_cp ≅ 7,35*10²²*0,003, resuelves y queda:

F_cp ≅ 2,005*10²⁰ N.

Espero haberte ayudado.

Te sugiero los videos de fuerza electromotriz...