-
Pablo
el 30/1/19Daniel Claros
el 30/1/19Antonio Silvio Palmitano
el 30/1/19Comienza por plantear la definición de la aceleración como función del tiempo:
a(t) = dv(t)/dt;
luego, propones el cambio de variable para expresar a la aceleración en función de la posición (observa que empleamos la Regla de la Cadena), y queda:
a(x) = (dv/dx)*(dx/dt),
sustituyes la expresión del último factor (observa que es la definición de la velocidad), y queda:
a(x) = (dv/dx)*v,
luego, separas variables, ordenas factores en el segundo miembro, y queda:
a(x)*dx = v*dv,
que es una ecuación equivalente a:
v*dv = a(x)*dx (1).
Luego, sustituyes la expresión de la aceleración que tienes en tu enunciado, y queda:
v*dv = (8 - 2*x2)*dx,
multiplicas por 2 en ambos miembros, y qeuda:
2*v*dv = 2*(8 - 2*x2)*dx,
distribuyes el factor común numérico en el segundo miembro, y queda:
2*v*dv = (16 - 4*x2)*dx,
integras en ambos miembros, y queda:
v2 = 16*x - 4*x3/3 + C (2);
luego, reemplazas el valor de la posición inicial (xi = 0) y de la velocidad inicial (vi = 0) para el instante inicial (ti = 0) que tienes en tu enunciado, cancelas términos nulos, y queda:
0 = C;
luego, reemplazas este valor en la ecuación señalada (2), cancelas el término nulo, extraes raíz cuadrada en ambos miembros, y queda:
v(x) = √(16*x - 4*x3/3) (3),
que es la expresión de la velocidad en función de la posición,
y observa (te dejo la tarea de determinarlo) que el dominio de la función velocidad es el intervalo:
Dv = [ 0 , √(12) ] (observa que consideramos solamente los valores positivo de la posición).
a)
Evalúas la expresión señalada (3) para la posición en estudio (x = 1), y queda:
v(1) = √(44/3) m/s ≅ 3,830 m/s.
b)
Derivas la expresión de la velocidad remarcada y señalada (3), y queda:
dv/dx = (16 - 4*x2)/( 2*√(16*x - 4*x3/3) ) (4),
y observa que esta función está definida en el intervalo abierto: D1 = ( 0 , √(12) );
luego, planteas la condición de valor estacionario (posible máximo o posible mínimo) de la función velocidad, y queda:
dv/dx = 0, sustituyes la expresión señalada (4), y queda:
(16 - 4*x2)/( 2*√(16*x - 4*x3/3) ) = 0, multiplicas en ambos miembros por 2*√(16*x - 4*x3/3), y queda:
16 - 4*x2 = 0, y de aquí tienes dos opciones:
1°)
x = -2, que no pertenece al dominio de la función velocidad;
2°)
x = 2, que sí pertenece al dominio de la función velocidad;
luego, evalúas la expresión de la velocidad para este valor estacionario, y para uno menor y otro mayor que él ( observa que elegimos a los valores extremos del dominio de dicha función: x = 0 y x = √(12) ), y tienes:
v( 0 ) = 0 (valor mínimo de la velocidad),
v( 2 ) = √(64/3) m/s ≅ 4,619 m/s (valor máximo de la velocidad),
v( √(12) ) = √(16*√(12) - 4*( √(12) )3/3) = √( 16*√(12) - 16*√(12) ) = √(0) = 0 (valor mínimo de la velocidad);
por lo que tienes que el valor mínimo de la velocidad es cero, y se corresponde con las posiciones:
x = 0, para el que la aceleración es: a( 0 ) = 8 - 2*02 = 8 - 0 = 8 m/s2; y
x = √(12) m, para el que la aceleración es: a( √(12) ) = 8 - 2*( √(12) )2 = 8 - 2*12 = 8 - 24 = -16 m/s2.
c)
Observa en el inciso anterior que el valor de la velocidad para el punto estacionario es el mayor, por lo que tienes que el valor máximo de la velocidad es:
v(2) = √(64/3) m/s, que corresponde a la posición: x = 2 m,
para el que la aceleración es: a(2) = 8 - 2*22 = 8 - 8 = 0.
Espero haberte ayudado.
-
Pregunta teorica de fisica.
Es un multiple choice y tengo dudas sobre la respuesta
Un observador mide la velocidad de un móvil al pasar por delante de él. Un tiempo después, otro observador (desde el mismo sistema de referencia que el anterior) mide la velocidad del mismo móvil. Si la velocidad que midieron ambos observadores es la misma, entonces:
a) Se conserva la Energía Mecánica. b) La variación de Energía Cinética es constante.c) El trabajo neto sobre el móvil es cero. d) La Energía Cinética es cero.
El punto d) lo descarto porque en la primer situacion el auto pasa por delante de el, es decir, tiene una cierta velocidad y lo ve pasar..Asumo que el 2do observador ve al auto a lo lejos, llendo con la misma velocidad, por lo cual su energia cinetica es distinta de cero.
El punto c) dice que el trabajo neto sobre el movil es cero, pero el auto se esta moviendo en linea recta (asumo nuevamente esto) entonces va a ser distinto de 0.
En cuanto a las opciones a) y b) creo que podrian ser ambas correctas...
En fin, nose si hay alguna trampa o hay alguna cosa teorica que se me haya pasado.
Cual seria la respuesta correcta?
-
Antonio Silvio Palmitano
el 29/1/19Observa que empleamos el Sistema Internacional de Unidades de Medida.
Tienes la densidad de masa del líquido (agua):
δL = 1000 Kg/m3.
Tienes los datos del cuerpo cilíndrico (corcho):
δC = 0,72 g/cm3 = 720 Kg/m3 (densidad de masa),
R = 2 cm = 0,02 m (radio de la base),
h = 5 cm (altura).
a)
Observa que sobre el cuerpo actúan dos fuerzas verticales cuando está completamente sumergido, de las que indicamos sus módulos y sentidos:
Peso: P = M*g = δC*VC*g, hacia abajo;
Empuje del líquido E = δL*VC*g, hacia arriba;
luego, planteas la expresión de la fuerza resultante (F) que actúa sobre el cuerpo (observa que consideramos positivo al sentido hacia arriba), y queda:
F = E - P, sustituyes expresiones, y queda:
F = δL*VC*g - δC*VC*g, extraes factores comunes, y queda:
F = (δL - δC)*VC*g, reemplazas los valores de las densidades de masas, y queda:
F = (1000 - 720)*VC*g, resuelves el primer factor, y queda:
F = 280*VC*g,
y observa que tienes una multiplicación de tres factores positivos, por lo que tienes que la fuerza resultante tiene sentido hacia arriba, por lo que puedes concluir que el cuerpo asciende cuando es liberado.
b)
Aplicas la Segunda Ley de Newton para el instante correspondiente al momento en el que el cuerpo es liberado, y tienes la ecuación:
F = MC*ai,
sustituyes la expresión de la fuerza resultante que tienes remarcada, y la expresión de la masa del cuerpo, y queda:
(δL - δC)*VC*g = δC*VC*ai, divides en ambos miembros por δC*VC, y queda:
(δL - δC)*g/δC = ai,
que es la expresión de la aceleración inicial del cuerpo, que corresponde al inicio de su ascenso al ser liberado (observa que de aquí en más la aceleración varía una vez que parte del cuerpo se encuentra fuera del líquido).
Luego, solo queda que reemplaces valores y hagas los cálculos.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 29/1/19Observa que las fuerzas: F, P y Q, cuyos módulos indicamos: F, P y Q, tienen las direcciones de los vectores: AD, AB y AC, respectivamente.
Luego, a partir de las coordenadas de los puntos: A, B, C y D que tienes representados en tu imagen, planteas las expresiones de los vectores indicados, y queda:
AD = < 0 , -8 , -12 >, cuyo módulo queda expresado: |AD| = √(208),
AB = < 6 , 8 , -12 >, cuyo módulo queda expresado: |AB| = √(244),
AC = < -6 , 6 , -12 >, cuyo módulo queda expresado: |AC| = √(216);
luego, planteas las expresiones de los vectores unitarios asociados a los tres vectores anteriores, y queda:
uF = AD/|AD| = < 0 , -8 , -12 >/√(208),
uP = AB/|AB| = < 6 , 8 , -12 >/√(244),
uQ = AC/|AC| = < -6 , 6 , -12 >/√(216),
y observa que estos tres vectores unitarios expresan las direcciones y los sentidos de las fuerzas aplicadas en el punto A,
cuyas expresiones vectoriales quedan (recuerda que tienes el valor del módulo de la fuerza F en tu enunciado):
F = F*uF = 120*< 0 , -8 , -12 >/√(208) = < 0 , -960 , -1440 >/√(208) (en libras),
P = P*uP = P*< 6 , 8 , -12 >/√(244) = < 6*P , 8*P , -12*P >/√(244) (en libras),
Q = Q*uQ = Q*< -6 , 6 , -12 >/√(216) = < -6*Q , 6*Q , -12*Q >/√(216) (en libras).
Luego, planteas la expresión de la fuerza resultante, y queda:
F + P + Q = R, sustituyes las expresiones de las fuerzas en el primer miembro, y queda:
< 0 , -960 , -1440 >/√(208) + < 6*P , 8*P , -12*P >/√(244) + < -6*Q , 6*Q , -12*Q >/√(216) = R,
resuelves las divisiones en todos los términos, y queda:
< 0 , -960/√(208) , -1440/√(208) > + < 6*P/√(244) , 8*P/√(244) , -12*P/√(244) > +
+ < -6*Q/√(216) , 6*Q/√(216) , -12*Q/√(216) > = R,
expresas a la fuerza resultante en función de sus componentes (observa que tiene la dirección del eje OZ, por lo que sus dos primeras componentes son iguales a cero, y observa que indicamos con A a su tercera componente), y queda:
< 0 , -960/√(208) , -1440/√(208) > + < 6*P/√(244) , 8*P/√(244) , -12*P/√(244) > +
+ < -6*Q/√(216) , 6*Q/√(216) , -12*Q/√(216) > = < 0 , 0 , A >;
luego, por suma e igualdad entre vectores, sumas componente a componente, y tienes el sistema de tres ecuaciones lineales de primer grado con tres incógnitas (P, Q y A):
6*P/√(244) - 6*Q/√(216) = 0,
-960/√(208) + 8*P/√(244) + 6*Q/√(216) = 0,
-1440/√(208) - 12*P/√(244) - -12*Q/√(216) = A;
y luego, queda que resuelvas el sistema de ecuaciones, y obtendrás los valores de los módulos de las fuerzas P y Q, y también el valor de la tercera componente (A) de la fuerza resultante (R).
Haz el intento de terminar la tarea, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.
-
¿un objeto puede aplicar una fuerza sobre si mismo?
Francisco Javier Tinoco Tey
el 28/1/19Un cuerpo no puede ejercer fuerza sobre sí mismo . Si se necesita que actúe una fuerza sobre mi persona, tendré que buscar algún otro cuerpo que ejerza una fuerza, porque no existe ninguna forma de que un objeto ejerza fuerza sobre sí mismo (yo no puedo empujarme, una pelota no puede "patearse" a sí misma).
-
PREGUNTA SOBRE DINÁMICA: Cuando hay dos cuerpos unidos por una cuerda en un plano horizontal. La fuerza de rozamiento de un cuerpo es la misma que la masa de ese mismo cuerpo pero en vez de kg en newtons??
Antonio Silvio Palmitano
el 28/1/19Vamos con una orientación, que esperamos te se de utilidad.
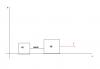
Considera la situación de la figura, en la que consideramos que el sistema se desplaza hacia la derecha.
1°)
Observa que sobre el bloque más pequeño actúan cuatro fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: P1 = M1*g, vertical, hacia abajo;
Acción normal del suelo: N1, vertical, hacia arriba;
Tensión de la cuerda: T, horizontal, hacia la derecha;
Rozamiento del suelo: fr1 = μ*N1, horizontal, hacia la izquierda;
luego, aplicas las Segunda Ley de Newton, y tienes el sistema de ecuaciones:
T - fr1 = M1*a,
N1 - P1 = 0,
sustituyes las expresiones de los módulos de las fuerzas, y queda:
T - μ*N1 = M1*a,
N1 - M1*g = 0, de aquí despejas: N1 = M1*g,
luego sustituyes la expresión remarcada en la primera ecuación, despejas, y queda:
T = μ*M1*g + M1*a (1).
2°)
Observa que sobre el bloque más grande actúan cinco fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: P2 = M2*g, vertical, hacia abajo;
Acción normal del suelo: N2, vertical, hacia arriba;
Tensión de la cuerda: T, horizontal, hacia la izquierda;
Rozamiento del suelo: fr2 = μ*N2, horizontal, hacia la izquierda;
Fuerza externa: F, horizontal, hacia la derecha;
luego, aplicas las Segunda Ley de Newton, y tienes el sistema de ecuaciones:
F - T - fr2 = M2*a,
N2 - P2 = 0,
sustituyes las expresiones de los módulos de las fuerzas, y queda:
F - T - μ*N2 = M2*a,
N2 - M2*g = 0, de aquí despejas: N2 = M2*g,
luego sustituyes esta última expresión remarcada en la primera ecuación, y queda:
F - T - μ*M2*g = M2*a (2).
Luego, como puedes apreciar, hemos considerado dos diagramas de fuerzas independientes, uno para cada cuerpo del sistema, y para resolver el problema solo queda que sustituyas la expresión señalada (1) en la ecuación señalada (2), y despejes la incógnita que tengas que resolver.
Espero haberte ayudado.
-
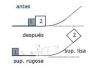
Dos bloques de masa m1 = 1,0 kg y m2 = 2,0 kg se encuentran inicialmente en reposo al pie de una rampa. Los bloques están unidos por una sustancia explosiva (de masa despreciable). En determinado momento, la sustancia explota haciendo que los bloques salgan despedidos en direcciones opuestas. El bloque 1 se frena a una distancia L = 0,5 m del lugar de la explosión debido a la fricción sobre la superficie rugosa de coeficiente de rozamiento cinético µk = 0,30. Calcule la altura h a la que llega el bloque 2 sobre la pendiente lisa antes de frenarse. Suponga que los bloques nunca se despegan del suelo.
Muchas gracias.
Antonio Silvio Palmitano
el 28/1/19Antonio Silvio Palmitano
el 28/1/19Tienes un sistema formado por los dos bloques, y tienes cuatro situaciones importantes:
a)
El sistema está a punto de explotar;
b)
La explosión recién ocurrió;
c)
El móvil (1) alcanza el reposo.
d)
El móvil (2) alcanza su altura máxima.
1°)
Planteas las expresiones del impulso (cantidad de movimiento) y de la energía mecánica en las dos primeras situaciones (observa que consideramos un sistema de referencia con eje OX horizontal con sentido positivo hacia la derecha, y con eje OY vertical con sentido positivo hacia arriba), y queda:
pa = 0 (los móviles están en reposo),
EMa = 0 (los móviles se encuentran con sus alturas iguales a cero y en reposo);
pb = M1*v1 + M2*v2 = 1*v1 + 2*v2,
EMb = EC1 + EC2 = (1/2)*M1*v12 + (1/2)*M2*v22 = (1/2)*1*v12 + (1/2)*2*v22 = (1/2)*v12 + 1*v22;
luego, como no actúan fuerzas exteriores al sistema en el plano de movimiento durante la explosión, puedes plantear que el impulso se conserva, y tienes la ecuación:
pb = pa, sustituyes expresiones, y queda:
1*v1 + 2*v2 = 0, y de aquí despejas:
v1 = -2*v2 (1).
2°)
Planteas la expresión de la energía mecánica en la situación (c), y tienes:
EMc = 0 (observa que el bloque más pequeño está en reposo al nivel de altura igual a cero);
luego, planteas la expresión del trabajo de la fuerza de rozamiento (observa que consideramos que el módulo de la aceleración gravitatoria terrestre es: g = 10 m/s2), y queda:
Wfr = -μk*N*L = -μk*M1*g*L = -0,30*1*10*0,5 = -1,5 J;
luego, planteas la ecuación energía mecánica-trabajo solamente para el bloque más pequeño, y queda:
EMc - EMb = Wfr, sustituyes expresiones, y queda:
0 - (1/2)*v12 = -1,5, y de aquí despejas:
v1 = -√(3) m/s ≅ -1,732 m/s, que es la expresión de la velocidad del bloque más pequeño inmediatamente después de la explosión (observa que esta velocidad tiene sentido hacia la izquierda);
luego, reemplazas este valor remarcado en la ecuación señalada (1), y queda:
-√(3) = -2*v2, y de aquí despejas:
v2 = √(3)/2 m/s ≅ 0,866 m/s, que es la expresión de la velocidad del bloque más grande inmediatamente después de la explosión (observa que esta velocidad tiene sentido hacia la derecha).
3°)
Planteas conservación de la energía entre las situaciones señaladas (b) (d) solamente para el bloque más grande, y queda:
EMd = EMb, sustituyes expresiones, y queda:
M2*g*h = (1/2)*M2*v22, divides por M2*g en ambos miembros, y queda:
h = (1/2)*v22/g, reemplazas el último valor remarcado, reemplazas el valor de la aceleración gravitatoria, y queda:
h = (1/2)*( √(3)/2 )2/10, resuelves, y queda:
h = 3/80 m = 0,0375 m, que es la expresión de la altura máxima que alcanza el bloque más grande sobre la rampa.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 28/1/19a)
Observa que tienes los puntos de la gráfica, cuya forma general es: P(t,x):
A1( 1,50 ; 8 ) (de aquí tienes: t1 = 1,50 s y x1 = 8 m),
A2( 4,00 ; 2 ) (de aquí tienes: t2 = 4,00 s y x2 = 2 m);
luego, planteas la expresión de la velocidad media entre los instantes indicados, y queda:
vm = (x2 - x1)/(t2 - t1), reemplazas valores, y queda:
vm = (2 - 8)/(4,00 - 1,50), resuelves los agrupamientos de términos, y queda:
vm = -6/2,50, resuelves, y queda:
vm = -2,4 m/s.
b)
Observa que la recta que tienes trazada en el gráfico cartesiano de tu enunciado pasa por los puntos:
B1( 2,00 ; 6 ) (de aquí tienes: t1 = 2 s y x2 = 6 m),
B2( 3,50 ; 0 ) (de aquí tienes: t2 = 3,50 s y x2 = 0 m);
luego, planteas la expresión de la pendiente del segmento determinado por dichos puntos, y queda:
m = (x2 - x1)/(t2 - t1), reemplazas valores, y queda:
m = (0 - 6)/(3,50 - 2,00), resuelves los agrupamientos de términos, y queda:
m = -6/1,50, resuelves, y queda:
m = -4, y como la recta es tangente a la gráfica en el punto correspondiente al instante en estudio (t1 = 2,00 s), entonces tienes que la velocidad instantánea del móvil en dicho instante es:
v(2,00) = -4 m/s.
c)
Observa que tienes el punto:
C( 4,00 , 2 ) (de aquí tienes: t = 4,00 s y x = 2 m),
en el cuál tienes que la recta tangente a la gráfica que tienes en tu enunciado es una recta paralela al eje Ot que pasa por dicho punto, por lo que tienes que su pendiente es igual a cero y, por lo tanto, tienes que la velocidad instantánea del móvil en el instante en estudio (t = 4,00 s) es nula:
v(4,00) = 0.
Espero haberte ayudado.
-
me podrían ayudar con este ejercicio
una mujer camina a una taza de 5 pi/seg a lo largo de un diámetro de un patio circular. Una luz ubicada en el extremo de un diámetro perpendicular al de su trayectoria proyecta una sombra sobre la pared circular. Que tan rápido se mueve la sombra a lo largo de la pared cuando la distancia de la mujer al centro del patio es de r/2 donde r [pie] es el radio del patio.
Antonio Silvio Palmitano
el 28/1/19Observa la primera imagen, en la que intentamos mostrarte los siguientes pasos:
1°)
Presentamos la circunferencia cuya ecuación cartesiana es:
x2 + y2 = r2,
que corresponde a la ubicación de la pared,
y determinamos dos puntos pertenecientes a ella: F(0,r) (ubicación del foco de luz), y S(x,y) (ubicación de la sombra de la mujer sobre la pared).
Presentamos la recta cuya ecuación es:
y = -(r/s)*x + r,
que corresponde al rayo luminoso que determina la sombra de la mujer sobre la pared.
Presentamos la posición de la mujer: M(s,0), y consideramos que se desplaza sobre el eje OX con el sentido positivo de dicho eje (observa que la coordenada s es negativa).
2°)
Presentamos el sistema de ecuaciones para establecer las coordenadas del punto de intersección de la circunferencia con la recta (punto S) (observa que el punto F también pertenece a ambas curvas).
3°)
Presentamos las expresiones de las derivadas con respecto al tiempo de las coordenadas del punto S (x' e y'), que corresponden a las componentes de la velocidad de desplazamiento de la sombra.
Observa la segunda imagen, en la que mostramos los siguientes pasos:
4°)
Evaluamos las expresiones x' e y' para la condición que tienes en tu enunciado:
s' = 5 p/s (tasa de desplazamiento, o rapidez del móvil),
s = r/2 (posición del móvil que tenemos en estudio);
y luego presentamos la expresión vectorial de la velocidad instantánea del móvil, calculamos su módulo.
Espero haberte ayudado.