-
Dos esferas pequeñas, idénticas y de masa m están cargadas eléctricamente con una q= 4 μC cada una.
Se suspenden del mismo punto, en presencia del campo gravitatorio, mediante hilos iguales de masa despreciable y longitud L= 0,4 m. ¿Cuál debe ser el valor de la masa m para que en equilibrio formen un ángulo de 60º?
Datos: k=9x109
Antonio Silvio Palmitano
el 3/2/19Antes que todo, disculpa la precariedad de la imagen, pero estamos un poco duros para los gráficos.
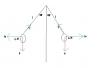
Observa que, como las dos esferas son idénticas, tienen cargas iguales, y están suspendidas con hilos idénticos, entonces tienes que las dos esferas quedan suspendidas y en equilibrio, con posiciones simétricas con respecto a la vertical que pasa por el punto desde donde están suspendidos los hilos.
Luego, considera la esfera de la derecha, sobre la que están aplicadas tres fuerzas, de las que indicamos sus módulos, direcciones y sentidos (observa que la distancia entre las esferas queda expresada: d = 2*L*senθ):
Peso: P = M*g, vertical, hacia abajo;
Fuerza electrostática: Fe = k*q*q/d2 = k*q2/(2*L*senθ)2 = k*q2/(4*L2*sen2θ), horizontal, hacia la derecha;
Tensión del hilo: T, inclinada hacia la izquierda y hacia arriba, según la dirección del hilo.
Luego, estableces un sistema de referencia cartesiano con origen de coordenadas en la posición de la carga en estudio, con eje OX horizontal con sentido positivo hacia la derecha, y con eje OY vertical con sentido positivo hacia arriba; luego, aplicas la Primera Ley de Newton, y tienes el sistema de ecuaciones:
Fe - T*senθ = 0, de aquí despejas: T*senθ = Fe (1),
T*cosθ - P = 0; de aquí despejas: T*cosθ = P (2);
luego, divides miembro a miembro la ecuación señaada (1) entre la ecuación señalada (2), y queda:
senθ/cosθ = Fe/P, aquí multiplicas por P en ambos miembros, y queda:
P*senθ/cosθ = Fe, aquí sustituyes las expresiones de los módulos de las fuerzas, y queda:
M*g*senθ/cosθ = k*q2/(4*L2*sen2θ), aquí multiplicas en ambos miembros por cosθ/senθ, y queda:
M*g = k*q2/(4*L2*senθ*cosθ), aquí divides por g en ambos miembros, y queda:
M = k*q2/(4*L2*senθ*cosθ*g),
que es la expresión de la masa de cada esfera, en función de los datos que tienes en tu enunciado, de la Constante de Coulomb, y del módulo de la aceleración gravitatoria terrestre.
Te dejo la tarea de reemplazar valores y hacer el cálculo.
Espero haberte ayudado.
-
Un objeto de masa m = 300 g se empuja contra un resorte horizontal de constante elástica K=200 N/m como indica la figura y se suelta desde el reposo. El radio del rizo ABCD mide R = 10 cm. La distancia horizontal L desde A hasta el extremo del resorte cuando éste presenta su longitud natural lo es de L = 1m. En el tramo horizontal el suelo es rugoso con un coeficiente de rozamiento cinético µ = 0.2. En cambio, el interior del rizo es liso y su rozamiento despreciable. Calcula la deformación mínima x del resorte para la cual el objeto viajará por el interior del rizo permaneciendo en contacto con el mismo todo el tiempo.Muchas gracias.
Antonio Silvio Palmitano
el 3/2/19Considera un sistema de referencia cartesiano, con eje OX horizontal a nivel del suelo y con sentido positivo hacia la izquierda, y con eje OY vertical con sentido positivo hacia arriba.
Vamos por pasos, y observa que planteamos varias situaciones de interés:
1)
El resorte está comprimido, el bloque está en reposo sobre el suelo, por lo que la energía mecánica es solo elástica, y su expresión es:
EM1 = (1/2)*k*x2 = (1/2)*200*x2 = 100*x2 (en Joules).
2)
El bloque sigue sobre el suelo y recién se despega del resorte, el resorte está relajado, por lo que la energía mecánica es solo cinética de traslación, observa que consideramos que entre las situaciones señaladas (1) (2) no hay rozamiento, y su expresión es:
EM2 = (1/2)*M*v22 = (1/2)*0,3*v22 = 0,15v22 (en Joules).
3)
El bloque sigue sobre el suelo, recién alcanza el punto A, por lo que la energía mecánica es solo cinética de traslación, pero observa que la fuerza de rozamiento dinámico ha realizado trabajo, y las expresiones de la energía mecánica, y del trabajo de la fuerza de rozamiento entre las situaciones señaladas (2) y (3) quedan (observa que consideramos que el módulo de la aceleración gravitatoria terrestre es: 10 m/s2):
EM3 = (1/2)*M*v32 = (1/2)*0,3*v32 = 0,15v32 (en Joules),
Wfr23 = -μ*N = -μ*M*g*L = -0,2*0,3*10*1 = -0,6 J.
4)
El bloque alcanza justo el punto C (observa que consideramos que apenas se desprende del rizo en el punto C, por lo que la acción normal del rizo en ese punto es nula), por lo que tienes que la energía mecánica es solo cinética de traslación, con la velocidad justa para la aceleración centrípeta que garantice que el bloque permanecerá con trayectoria circunferencial, y también potencial gravitatoria, y las expresiones de la energía mecánica y de la aceleración centrípeta, que solo es la aceleración gravitatoria terrestre ya que la única fuerza aplicada sobre el bloque es su peso, quedan:
EM4 = (1/2)*M*v42 + M*g*(2*R) = (1/2)*0,3*v42 + 0,3*10*(2*0,1) = 0,15*v42 + 0,6 (en Joules),
acp4 = g, aquí sustituyes la expresión de la aceleración centrípeta, y queda:
v42/R = g, reemplazas los valores del radio del rizo y de la aceleración gravitatoria terrestre, y queda:
v42/0,1 = 10, multiplicas por 0,1 en ambos miembros, y queda:
v42 = 1, extraes raíz cuadrada positiva en ambos miembros, y queda:
v4 = 1 m/s, reemplazas este valor en la expresión de la energía mecánica para esta situación, y queda:
EM4 = 0,15*12 + 0,6 = 0,15*1 + 0,6 = 0,15 + 0,6 = 0,75 J.
Luego, planteas conservación de la energía mecánica entre las situaciones señaladas (1) (2) y entre las situaciones señaladas (3) (4), y planteas la ecuación trabajo-energía entre las situaciones señaladas (2) (3), y tienes las ecuaciones:
EM2 = EM1,
EM4 = EM3,
Wfr23 = EM3 - EM2;
luego, reemplazas las expresiones remarcadas en la primera y en la segunda ecuación , todo en la tercera ecuación, y queda:
Wfr23 = EM4 - EM1,
aquí reemplazas valores y sustituyes expresiones que ya tienes determinadas, y queda:
-0,6 = 0,75 - 100*x2,
aquí sumas 100*x2 y sumas 0,6 en ambos miembros, y queda:
100*x2 = 1,35,
aquí divides por 100 en ambos miembros, y queda:
x2 = 0,0135,
aquí extraes raíz cuadrada positiva en ambos miembros, y queda:
x ≅ 0,116 m.
Espero haberte ayudado.
-
 En el último apartado de un ejercicio de campo eléctrico me piden que halle la diferencia de potencial que hay entre la posición de equilibrio y la posición vertical de una carga. El gráfico del ejercicio es la siguiente:
En el último apartado de un ejercicio de campo eléctrico me piden que halle la diferencia de potencial que hay entre la posición de equilibrio y la posición vertical de una carga. El gráfico del ejercicio es la siguiente:Antonio Silvio Palmitano
el 3/2/19Si tienes la longitud del hilo (L), y como el campo es constante y tiene dirección horizontal con sentido positivo hacia la derecha, entonces tienes que la diferencia de potencial que pides queda expresada:
ΔV = E*L*senθ,
donde θ es la medida del angulo que forma el hilo con la dirección vertical, que tienes señalado en tu gráfico, y que seguramente ya has calculado cuando planteaste la condición de equilibrio.
Luego, si no tienes la longitud del hilo entre los datos, o no la has podido calcular en los incisos anteriores del problema, por favor envía una foto del enunciado completo para que podamos darte una mano.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 3/2/19Observa que sobre el taco están aplicadas cuatro fuerzas, de las que indicamos sus módulos, direcciones y sentidos (consideramos que el módulo de la aceleración gravitatoria terrestre es: g = 10 m/s2):
Peso: PT = MT*g = 0,5*10 = 5 N, vertical, hacia abajo;
Acción normal de la mesa: N, vertical, hacia arriba;
Tensión de la cuerda, T, horizontal, hacia la derecha,
Rozamiento dinámico de la mesa: fr = μ*N, horizontal, hacia la izquierda;
luego, estableces un sistema de referencia con eje OX horizontal con sentido positivo hacia la derecha, y con eje OY vertical con sentido positivo hacia arriba, aplicas la Segunda Ley de Newton, y tienes el sistema de ecuaciones:
T - fr = M*a,
N - PT = 0;
luego, sustituyes las expresiones de los módulos de las fuerzas, y queda:
T - μ*N = M*a,
N - 5 = 0, aquí sumas 5 en ambos miembros, y queda: N = 5 N;
luego, reemplazas el valor remarcado y los valores que tienes en tu enunciado en la primera ecuación, y queda:
T - 0,25*5 = 0,5*a, y de aquí despejas:
T = 0,5*a + 1,25 (1).
Observa que sobre la pesa están aplicadas dos fuerzas verticales, de las que indicamos sus módulos, y sentidos (consideramos que el módulo de la aceleración gravitatoria terrestre es: g = 10 m/s2):
Peso: Pp = Mp*g = 0,25*10 = 2,5 N, vertical, hacia abajo;
Tensión de la cuerda, T, vertical, hacia la arriba;
luego, aplicas la Segunda Ley de Newton, y tienes la ecuación (observa que consideramos un sistema de referencia con eje OY vertical con sentido positivo hacia abajo):
Mp*g - T = Mp*a, reemplazas valores que tienes en tu enunciado, y queda:
0,25*10 - T = 0,25*a, y de aquí despejas:
T = 2.5 - 0,25*a (2).
Luego, igualas las expresiones señaladas (1) (2), y queda:
2.5 - 0,25*a = 0,5*a + 1,25, aquí restas 0,5*a y restas 2,5 en ambos miembros, y queda:
-0,75*a = -1,25, divides por -0,75 en ambos miembros, y queda:
a ≅ 1,667 m/s2.
Luego, reemplazas el valor remarcado en las ecuaciones señaladas (1) (2), resuelves, y queda:
T ≅ 2,083 N.
Espero haberte ayudado.
-
Hola! necesito ayuda con este ejercicio: Usted vuela al este con una avioneta que vigila el tráfico sobre una autopista. Los accidentes del terreno le indican que su rapidez es 60 m/s relativa a la tierra y su indicador de rapidez en el aire también indica 60 m/s, pero la nariz del avión apunta un poco al sur del este, y el meteorólogo dice que sopla un viento de 20 m/s. a) en qué dirección sopla el viento? b) Qué dirección debe fijar el piloto para sobrevolar siempre la autopista?
Raúl RC
el 3/2/19Te recomiendo veas estos vídeos, te ayudarán mucho, nos cuentas ;)
https://www.youtube.com/watch?v=oz5Mwh4_Co4
https://www.youtube.com/watch?v=n7GpTF6Dj5w&t=409s
-
La intensidad del campo electrico en que se mide??? En N/C , en N/m o V/m, porque en cada sitio pone un diferente.
Antonio Silvio Palmitano
el 1/2/19Antonio Silvio Palmitano
el 1/2/19Luego, si multiplicas al numerador y al denominador por m (metro), la expresión de la unidad de intensidad de campo electrostático queda:
[E] = N*m/(C*m) = (N*m/C)/m = (J/C)/m;
luego, observa que la expresión del agrupamiento es equivalente a Voltio, por lo que tienes la unidad internacional equivalente:
[E] = V/m.
Espero haberte ayudado.
-
Hola buenas, me han mandado este ejercicio de física y no soy capaz de resolverlo.Me podrían ayudar ?
Un costal de arena de 3 kg se encuentra colgando de un hilo fuerte de longitud 0,75 m.Sobre el costal se dispara un fusil cuya bala tiene una mas de 50 gr.La bala atraviesa el costaly recorre una distancia horizontal de 25 mantes de golpear el sueloque se encuentra a una altura de 1,3 m por debajo del impacto en el costal.Calula a) la velocidad de la bala después del choque b)la velocidad del costal después del choque c) la velocidad de la bala antes del choque d)la energía perdida al atravesar la bala el costal
Muchas gracias, es que solo he sido capaz de resolver el a y ni siquiera se si estará bien
-
Antonio Silvio Palmitano
el 1/2/19Te ayudo con el planteo del problema.
Establece un sistema de referencia con eje OX horizontal con sentido positivo hacia la derecha según tu imagen, y con eje OY vertical con sentido positivo hacia arriba.
Luego, vamos por pasos:
a)
Observa que sobre el bloque A actúan cinco fuerzas, de las que indicamos sus módulos, direcciones y sentidos, y observa también que el bloque B "de opone" al desplazamiento del bloque A hacia la derecha:
Peso: PA = MA*g, vertical, hacia abajo;
Acción normal del suelo: NA, vertical, hacia arriba;
Rozamiento del suelo: frA = μA*NA, horizontal hacia la izquierda;
Fuerza externa: F = 150 N, inclinada 30º con respecto al semieje OX positivo, hacia arriba;
Acción normal del bloque B sobre el bloque A: NAB, horizontal, hacia la izquierda;
luego, aplicas la Segunda Ley de Newton (observa que sustituimos las expresiones de los módulos de las fuerzas), y tienes el sistema de ecuaciones:
F*cos(30º) - NAB - μA*NA = MA*a,
F*sen(30º) + NA - MA*g = 0, de aquí despejas:
NA = MA*g - F*sen(30º);
luego, sustituyes esta última expresión remarcada en la primera ecuación, y queda:
F*cos(30º) - NAB - μA*( MA*g - F*sen(30º) ) = MA*a, distribuyes el tercer término, y queda:
F*cos(30º) - NAB - μA*MA*g + μA*F*sen(30º) = MA*a, y de aquí despejas:
NAB = F*cos(30º) + μA*F*sen(30º) - μA*MA*g - MA*a (1).
b)
Observa que sobre el bloque B actúan cuatro fuerzas, de las que indicamos sus módulos, direcciones y sentidos, y observa también que el bloque A "empuja" al bloque B hacia la derecha:
Peso: PB = MB*g, vertical, hacia abajo;
Acción normal del suelo: NB, vertical, hacia arriba;
Rozamiento del suelo: frB = μB*NB, horizontal hacia la izquierda;
Reacción normal del bloque A sobre el bloque B: NAB, horizontal, hacia la derecha;
luego, aplicas la Segunda Ley de Newton (observa que sustituimos las expresiones de los módulos de las fuerzas), y tienes el sistema de ecuaciones:
NAB - μB*NB = MB*a,
NB - MB*g = 0, de aquí despejas:
NB = MB*g;
luego, sustituyes esta última expresión remarcada en la primera ecuación, y queda:
NAB - μB*MB*g = MB*a, y de aquí despejas:
NAB = μB*MB*g + MB*a (2).
c)
Igualas las expresiones señaladas (2) (1), y queda:
μB*MB*g + MB*a = F*cos(30º) + μA*F*sen(30º) - μA*MA*g - MA*a,
aquí sumas MA*a y restas μB*MB*g en ambos miembros, y queda:
MA*a + MB*a = F*cos(30º) + μA*F*sen(30º) - μA*MA*g - μB*MB*g,
extraes factor común en el primer miembro, extraes factor común en los dos primeros términos y en los dos términos que ses siguen en el segundo miembro, y queda:
(MA + MB)*a = F*( cos(30º) + μA*sen(30º) ) - (μA*MA + μB*MB)*g,
divides por (MA + MB) en ambos miembros, y queda:
a = [ F*( cos(30º) + μA*sen(30º) ) - (μA*MA + μB*MB)*g ] / (MA + MB),
que es la expresión de la aceleración del sistema de dos bloques, en función de los datos que tienes en tu enunciado y del módulo de la aceleración gravitatoria terrestre.
Luego, solo queda que reemplaces valores y hagas el cálculo.
Espero haberte ayudado.
-
Dos vectores de módulos respectivamente iguales a 4u y 10u forman entre si un ángulo de 150 grados. El angulo entre el vector suma y el vector de mayor modulo es aproximadamente? Ayuda por favor no sé el proceso a seguir :(
Antonio Silvio Palmitano
el 1/2/19Comenzamos por designar con a y b a los vectores, y tienes los datos:
│a│ = 4 u,
│b│ = 10 u,
θ = 150º.
Luego, planteas la expresión del producto escalar entre los dos vectores, y queda:
a•b = │a│*│b│*cosθ = (4 u)*(10 u)*cos(150º) = (40 u2)*(-√(3)/2) = -20*√(3) u2 (1).
Luego, planteas la expresión de los productos escalares de cada vector por sí mismo, y queda:
a•a = │a│*│a│*cos(0º) = (4 u)*(4 u)*1 = 16 u2 (2);
b•b = │b│*│b│*cos(0º) = (10 u)*(10 u)*1 = 100 u2 (3).
Luego, planteas la expresión del cuadrado del módulo del vector suma en función del producto escalar de dicho vector por sí mismo, y queda:
│a + b│2 = (a + b)•(a + b),
distribuyes y reduces términos semejantes en el segundo miembro, y queda:
│a + b│2 = a•a + 2*(a•b) + b•b,
reemplazas los valores señalados (2) (1) (3), y queda:
│a + b│2 = 16 u2 + 2*(-20*√(3) u2 ) + 100 u2,
resuelves el segundo término, reduces términos semejantes, extraes la expresión de la unidad de medida como factor común, y queda:
│a + b│2 = ( 116 - 40*√(3) ) u2,
extraes raíz cuadrada en ambos miembros, y queda:
│a + b│ = √( ( 116 - 40*√(3) ) u2 ),
extraes la expresión de la unidad de medida fuera de la raíz, y queda:
│a + b│ = √( 116 - 40*√(3) ) u (4).
Luego, planteas la expresión del producto escalar del vector (a + b) por el vector b, y queda:
│a + b│*│b│*cosφ = (a + b)•b,
distribuyes el segundo miembro, y queda:
│a + b│*│b│*cosφ = a•b + b•b,
sustituyes las expresiones señaladas (4), el valor del módulo del vector b, las expresiones señaladas (1) (3), y queda:
(√( 116 - 40*√(3) ) u) * (10 u) * cosφ = -20*√(3) u2 + 100 u2,
cancelas la expresión de la unidad de medida en todos los términos, y queda:
√( 116 - 40*√(3) ) * 10 * cosφ = -20*√(3) + 100,
divides por 10 en todos los términos de esta ecuación, y queda:
√( 116 - 40*√(3) ) * cosφ = -2*√(3) + 10,
divides por √( 116 - 40*√(3) ) en ambos miembros, y queda:
cosφ = (-2*√(3) + 10) / √( 116 - 40*√(3) ) (5),
que es la expresión del coseno del ángulo determinado por el vector b y el vector (a + b).
Luego, resuelves el segundo miembro de la ecuación señalada (5), y queda:
cosφ ≅ 0,956232,
aquí compones en ambos miembros con la función inversa del coseno, y queda:
φ ≅ 17,014º,
que es el valor aproximado de la medida del ángulo que determina el vector suma con el vector b.
Espero haberte ayudado.