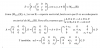Comienza por plantear la continuidad de la función en el valor x = 0, por medio de la definición:

1°)

f(0) = 3;

2°)

Lím(x→0+) f(x) = Lím(x→0+) (-x²+3x+a) = a;

3°)

la función es continua en x = 0, con la condición: a = 3;

y la expresión de la función queda, hasta ahora:

f(x) =

3                         si x = 0,

-x²+3x+3           si 0 < x < 1,

mx+b                si 1 ≤ x ≤ 2.

Luego, planteas la continuidad de la función en el valor x = 1, por medio de la definición:

1°)

f(1) = m(1) + b = m + b;

2°)

Lím(x→1-) f(x) = Lím(x→1-) (-x²+3x+3) = 5,

Lím(x→1+) f(x) = Lím(x→1+) (mx+b) = m+b;

3°)

la función es continua en x = 1, con la condición: m + b = 5, aquí restas m en ambos miembros, y queda: b = 5 - m (1);

y la expresión de la función queda, hasta ahora:

f(x) =

3                         si x = 0,

-x²+3x+3           si 0 < x < 1,

mx+5-m            si 1 ≤ x ≤ 2;

y hasta ahora, tienes que la función es continua en el intervalo cerrado [0,2].

Luego, plantea la expresión de la función derivada, y queda:

f ' (x) =

-2x+3                       si 0 < x < 1,

a determinar         si x = 1,

m                             si  1 < x < 2;

luego, planteas los límites laterales para x tendiendo al punto de corte (x = 1), y tienes:

Lím(x→1-) f ' (x) = Lím(x→1-) (-2x+3) = 1,

Lím(x→1+) f(x) = Lím(x→1+) m = m,

y tienes que el límite existe con la condición: m = 1;

luego, asignas este último valor a la derivada de la función en el punto de corte, y l expresión de la función derivada queda:

f ' (x) =

-2x+3                       si 0 < x < 1,

1                              si x = 1,

1                              si  1 < x < 2,

y observa que la función derivada está definida en el intervalo abierto (0,2).

Luego, reemplazas el último valor remarcado en la ecuación señalada (1), y queda: b = 4;

y con todos los valores remarcados, tienes que la expresión de la función queda:

f(x) =

3                         si x = 0,

-x²+3x+3           si 0 < x < 1,

x+4                    si 1 ≤ x ≤ 2,

y observa que la función es continua en el intervalo cerrado [0,2], y que es derivable en el intervalo abierto (0,2), por lo que tienes que se cumplen las dos hipótesis del Teorema del Valor Medio.

Luego, planteas la expresión de la razón de cambio promedio de la función entre los extremos del intervalo cerrado, y tienes:

( f(2) - f(0) ) / (2 - 0) = (6 - 3)/2 = 3/2;

luego, planteas la expresión de la tesis del Teorema del Valor Medio, y queda:

f ' (c) = ( f(2) - f(0) ) / (2 - 0),

sustituyes el último valor que hemos calculado en el segundo miembro, y queda:

f ' (c) = 3/2 (2);

luego, observa que los dos últimos trozos de la expresión de la función derivada no verifican esta ecuación, por lo que sustituyes la expresión del primer trozo de su expresión, y queda:

-2c + 3 = 3/2, aquí restas 3 en ambos miembros, y queda:

-2c = -3/2, aquí divides por -2 en ambos miembros, y queda: c = 3/4,

que pertenece al dominio de la función, que corresponde evaluarlo en el primer trozo de su expresión, por lo que es el valor para el cuál se verifica el Teorema del Valor Medio.

Espero haberte ayudado.

Observa que las expresiones de los tres trozos corresponden a funciones continuas, por lo que solo debes estudiar, por medio de la definición, la continuidad de la función en los valores de corte: x = 0 y x = 1.

Para x = 0:

1°)

f(0) = 0 (observa que corresponde evaluar este valor en el segundo trozo);

2°)

planteas los límites laterales, y tienes:

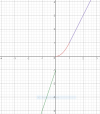
Lím(x→0-) f(x) = Lím(x→0-) (3x-1) = -1,

Lím(x→0+) f(x) = Lím(x→0+) (x²) = 0,

por lo que tienes que la función no tiene límite para x tendiendo a 0, porque los límites laterales existen pero son distintos;

3°)

tienes que la gráfica de la función es discontinua esencial (o inevitable) en x = 0, y tienes que la gráfica presenta un salto en este valor.

Para x = 1:

1°)

f(1) = 1 (observa que corresponde evaluar este valor en el segundo trozo);

2°)

planteas los límites laterales, y tienes:

Lím(x→1-) f(x) = Lím(x→1-) (x²) = 1,

Lím(x→1+) f(x) = Lím(x→1+) (2x-1) = 1,

por lo que tienes que la función si tiene límite para x tendiendo a 1, porque los límites laterales existen y coinciden;

3°)

tienes que la gráfica de la función es continua en x = 1, porque el valor de la función y el límite de la función coinciden para este valor.

Espero haberte ayudado.

Descomposición factorial

Muchas gracias Antonio! Por casualidad sabrás si en unicoos hay algún video que expliquen algún ejercicio parecido?

Creo que no.

Vamos con una orientación.

Tienes la expresión de la función derivada:

f ' (x) = 1, a la que corresponde la expresión general de la función:

f(x) = x + C (1).

Evalúas la expresión de la función señalada (1) para x = a, y queda:

f(a) = a + C, aquí restas a en ambos miembros, y queda:

f(a) - a = C, luego sustituyes en la expresión de la función señalada (1), y queda:

f(x) = x + f(a) - a, aquí conmutas los dos últimos términos, y queda:

f(x) = x - a + f(a).

Espero haberte ayudado.