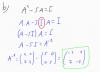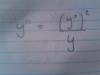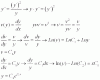-
Hola! me gustaria que me ayudasen en este problema de probabilidad... sobre todo con el apartado b2
El tiempo de duracion de las llamadas telefonicas a cierta centralita se distribuye segun una distribucion
normal de media 5 minutos y varianza 4. Calcula razonadamente:
b1) La probabilidad de que una llamada dure menos de 4,5 minutos. b2) El tiempo de duracion que no es superado por el 33 % de las llamadas.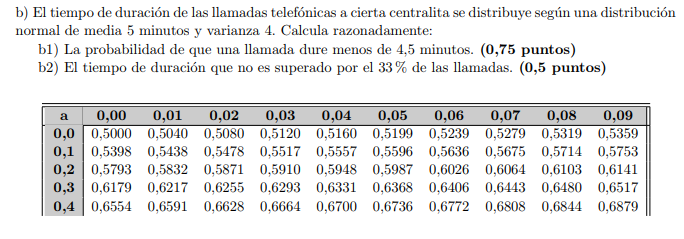
-
Hola buenos días. No entiendo una cosa del apartado B del ejercicio.

De dónde sale la I que he redondeado en rojo? Gracias!
Alexandre Muñoz
el 29/5/18Quieres sacar factor común la matriz A, por la dcha o por izquierda. Cuando queremos sacar factor común el 2 en esta expresión:
4x+2 = 2*(2x+1)
ponemos el 1, porque es la unidad (x*1=x para todo x). En matrices, la unidad es la matriz identidad ( I ) pues
A^2+A =A*(A+I)
-
Antonio Silvio Palmitano
el 29/5/18Puedes plantear la sustitución:
y ' = p.
Luego, derivas con respecto a x, y queda:
y ' ' = dp/dx = (dp/dy)*(dy/dx) = (dp/dy)*y ' = sustituyes = (dp/dy)*p = p*dp/dy.
Luego, tienes la ecuación diferencial de tu enunciado:
y ' ' = (y ')2/y,
sustituyes las expresiones remarcadas, y queda:
p*dp/dy = p2/y,
divides por p en ambos miembros, y queda
dp/dy = p/y,
separas variables, y queda:
(1/p)*dp = (1/y)*dy,
integras en ambos miembros, y queda:
ln(p) = ln(y) + c,
escribes a la constante c como un logaritmo de otra constante positiva, y queda:
ln(p) = ln(y) + ln(C),
aplicas la propiedad del logaritmo de una multiplicación en el segundo miembro, y queda:
ln(p) = ln(C*y),
compones en ambos miembros con la función inversa del logaritmo natural, y queda:
p = C*y;
luego, sustituyes la primera expresión remarcada, y queda:
dy/dx = C*y,
separas variables, y queda:
(1/y)*dy = C*dx,
integras, y queda:
ln(y) = C*x + d,
escribes a la constante d como el logaritmo de otra constante positiva, y queda:
ln(y) = C*x + ln(D),
compones en ambos miembros con la función inversa del logaritmo natural, y queda:
y = eC*x+ln(D),
aplicas la propiedad de la multiplicación de potencias con bases iguales, y queda:
y = eC*x * eln(D),
resuelves la composición entre funciones inversas en el segundo factor, ordenas factores, y queda:
y = D*eC*x,
que es la solución general explícita de la ecuación diferencial de segundo orden que tienes en tu enunciado.
Luego, puedes plantear las expresiones de las funciones derivadas primera y segunda, y queda:
y ' = C*D*eC*x,
y ' ' = C2*D*eC*x;
luego, planteas la expresión del segundo miembro de la ecuación diferencial de tu enunciado, y tienes:
( y ' )2 / y = sustituyes expresiones, y queda:
= ( C*D*eC*x )2 / ( D*eC*x ) = distribuyes el exponente en el numerador, y queda:
= C2*D2*( eC*x )2 / ( D*eC*x ) = simplificas, y queda:
= C2*D*eC*x = y ' '.
Espero haberte ayudado.
-
Hola.,, estoy empezando con geometría analítica y no entiendo ni jota.. por dónde debo empezar?
Carlos Flores
el 29/5/18Hola pvdk
Te recomiendo que veas los siguientes enlaces:
https://www.unicoos.com/video/matematicas/3-eso/rectas-y-vectores/aplicaciones-geometricas/geometria-en-el-plano-01
Saludos
-
-
Buenas, no sé cómo hacer el APARTADO C. Si alguien me pudiera ayudar se lo agradecería muchísimo.
Tengo el examen en unas horas :(
Antonio Silvio Palmitano
el 29/5/18Recuerda que el baricentro de un triángulo es el punto de intersección entre sus medianas.
Luego, planteas las expresiones de los puntos medios de los lados (te dejo los cálculos), y queda:
MAB(3,2), MAC(-1/2,2), MBC(7/2,5).
Luego, planteas las ecuaciones de las medianas del triángulo con cada uno de los puntos medios y sus vértices opuestos correspondientes (te dejo los planteos y los cálculos):
mAB-C: y = -x + 5;
mAC-B: y = (2/5)x + 11/5;
mBC-A: y = (4/3)x + 1/3.
Luego, puedes plantear la intersección entre las dos primeras medianas, para ello igualas expresiones, y queda:
(2/5)x + 11/5 = -x + 5, multiplicas por 5 en todos los términos de la ecuación, y queda:
2x + 11 = -5x + 25, sumas 5x y restas 11 en ambos miembros, y queda:
7x = 14, divides por 7 en ambos miembros, y queda:
x = 2, luego reemplazas en las ecuaciones de las dos primeras medianas, y en ambas queda: y = 3,
por lo que tienes que el punto de intersección entre ellas queda expresado: H(2,3);
y puedes reemplazar sus coordenadas en la ecuación de la tercera mediana, y verás que te queda una identidad verdadera: 3 = 3, por lo que tienes que el punto H también pertenece a las tercera mediana, por lo que tienes que el punto H(2,3) es el baricentro del triángulo.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 29/5/18Tienes la expresión de la función, que es continua y derivable en su dominio: D = R:
f(x) = 4*sen(2x) - 2.
Luego, observa que el segundo factor del primer término está comprendido entre -1 y 1, por lo que pudes plantear la doble inecuación:
-1 ≤ sen(2x) ≤ 1, multiplicas por 4 en los tres miembros, y queda:
-4 ≤ 4*sen(2x) ≤ 4, restas 2 en los tres miembros, y queda:
-6 ≤ 4*sen(2x) - 2 ≤ 2, sustituyes la expresión de la función en el miembro central, y queda:
-6 ≤ f(x) ≤ 2, por lo que tienes que la imagen de la función es el intervalo: [ -6 , 2 ].
Luego, planteas la expresión de la función derivada primera, y queda:
f ' (x) = 8*cos(2x) (1).
Luego, planteas la expresión de la función derivada segunda, y queda:
f ' ' (x) = -16*sen(2x) (2).
Luego, planteas la condición de punto crítico (posible mínimo o posible máximo), y queda:
f ' (x) = 0, sustituyes la expresión señalada (1), y queda:
8*cos(2x) = 0, divides por 8 en ambos miembros, y queda:
cos(2x) = 0, compones en ambos miembros con la función inversa del coseno, y queda:
2x = (2k-1)π/2, divides por 2 en ambos miembros de la ecuación, y queda:
x = (2k-1)π/4, con k ∈ Z;
luego, evalúas para distintos valores del parámetro k (por ejemplo -2, -1, 0, 1, 2, 3), y queda:
x = -5π/4, que no pertenece al intervalo indicado;
x1 = -3π/4, que si pertenece al intervalo indicado;
x2 = -π/4, que si pertenece al intervalo indicado;
x3 = π/4, que si pertenece al intervalo indicado;
x4 = 3π/4, que si pertenece al intervalo indicado;
x5 = 5π/4, que no pertenece al intervalo.
Luego, evalúas la expresión de la función derivada segunda para los valores remarcados, y queda:
f ' ' (-3π/4) = -16*sen(-3π/2) = -16*1 = -16 < 0;
f ' ' (-π/4) = -16*sen(-π/2) = -16*(-1) = 16 > 0;
f ' ' (π/4) = -16*sen(π/2) = -16*1 = -16 < 0;
f ' ' (3π/4) = -16*sen(3π/2) = -16*(-1) = 16 > 0;
luego, tienes que la gráfica de la función es cóncava hacia arriba en los puntos: x2 = -π/4 y x4 = 3π/4, por lo que tienes que la gráfica de la función presenta mínimos para estos valores;
luego, tienes que la gráfica de la función es cóncava hacia abajo en los puntos: x1 = -3π/4 y x3 = π/4, por lo que tienes que la gráfica de la función presenta máximos para estos valores.
Espero haberte ayudado.
-
Hola me podrían ayudar con este ejercicio por favor: Determine los valores de x ∈ [0, 2π] para los cuales se cumple: 1 + cos(x) + cos(2x) + cos(3x) = 0.
Antonio
el 28/5/181 + cos(x) + cos(2x) + cos(3x) = 0
1 + cos(x) + [cos2(x)-sen2(x)] + [4cos3(x)-3cos(x)] = 0
1 + cos(x) + cos2(x)-sen2(x) + 4cos3(x)-3cos(x) = 01 + cos(x) + cos2(x)-[1-cos2(x)] + 4cos3(x)-3cos(x) = 0
1 + cos(x) + cos2(x)-1+cos2(x) + 4cos3(x)-3cos(x) = 0
cos(x) + cos2(x)+cos2(x) + 4cos3(x)-3cos(x) = 0-2cos(x) + 2cos2(x)+ 4cos3(x) = 0
sea t=cos(x)
-2t + 2t2+ 4t3 = 0
Resolvemos esta ecuación de tercer grado:
t=0, t=-1 ^ t=1/2
con t=0 => cos(x)=0 => x=π/2 ^ x=3π/2
con t=-1 => cos(x)=-1 => x=π
con t=1/2 => cos(x)=1/2 => x=π/3 ^ x=-π/3
por lo tanto:
x ∈ { π/2, 3π/2, π, π/3, -π/3 }
-