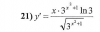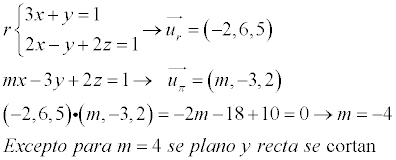-
Buenos días. Mi profesor me pidió generar dos matrices A y B cualesquiera (ambas 2X2) que sean conmutables y cuyos componentes sean distintos de 0 y de 1. Sé que en algún punto debo igualar pero me pierdo un poco. Gracias de antemano.
-
Hola! Una pregunta rápida por favor. ¿Me pod
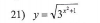 ríais ayudar con esta derivada? Tengo la solución pero no consigo sacar el procedimiento
ríais ayudar con esta derivada? Tengo la solución pero no consigo sacar el procedimientoAntonius Benedictus
el 27/5/18Antonio Silvio Palmitano
el 27/5/18Observa que puedes "trabajar" la expresión de la función, para luego derivarla con mayor facilidad.
y = √(3x^2+1) = (3x^2+1)1/2 = 3(1/2)(x^2+1) = 3(1/2)x^2+1/2 (*).
Luego, observa que debes aplicar la Regla de la Cadena ( recuerda que para derivar una expresión de una función del tipo 3u, tienes que la expresión de su función derivada queda: 3uln(3)*u ' ), por lo que tienes:
y ' = 3(1/2)x^2+1/2*x*ln(3),
que es una expresión equivalente a la que tienes consignada en tu solucionario, y para llevarla a dicha forma, multiplicas y divides por 3(1/2)x^2+1/2, y queda:
y ' = 3(1/2)x^2+1/2*3(1/2)x^2+1/2*x*ln(3) / 3(1/2)x^2+1/2,
resuelves la multiplicación entre los dos primeros factores del numerador (observa que tienes una multiplicación de potencias con bases iguales, por lo que tienes que sumar los exponentes), y queda:
y ' = 3x^2+1*x*ln(3) / 3(1/2)x^2+1/2,
sustituyes la primera expresión remarcada y señalada (*) en el denominador, y queda:
y ' = 3x^2+1*x*ln(3) / √(3x^2+1),
que es la expresión que tienes consignada en tu solucionario.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 27/5/18Tienes la expresión de una función diferenciable en R2, que es una composición entre dos funciones diferenciables:
g(x,y) = e1-4x^2-y (1).
a)
Planteas la ecuación general de las curvas de nivel, y queda:
e1-4x^2-y = k (observa que k toma valores estrictamente positivos);
luego, compones en ambos miembros con la función logarítmica natural, y queda:
1 - 4x2 - y = ln(k),
restas 1 y sumas 4x2 en ambos miembros, y queda:
-y = 4x2 - 1 + ln(k),
multiplicas por -1 en todos los términos de la ecuación, y queda:
y = -4x2 + 1 - ln(k),
que es la ecuación general de una familia de parábolas con eje OY negativo, y cuyos vértices quedan expresados: V( 0,1-ln(k) ); por lo que solo queda que reemplaces valores y hagas los gráficos de las curvas de nivel que te piden en tu enunciado (te dejo la tarea).
b)
Planteas las expresiones de las funciones derivadas parciales, y quedan:
gx(x,y) = e1-4x^2-y * (-8x) = -8x*e1-4x^2-y,
gy(x,y) = e1-4x^2-y * (-1) = -e1-4x^2-y;
luego, evalúas las expresiones de las funciones derivadas parciales para el punto en estudio, y quedan:
gx(1/2,0) = -4,
gy(1/2,0) = -1;
por lo que tienes que el vector gradiente de la función evaluado en el punto en estudio queda expresado:
∇g(1/2,0) = < -4 , -1 >.
c)
Tienes el vector dirección: v = < 4 , 0 >, cuyo módulo es: |v| = 4, y cuyo vector unitario asociado queda expresado: V = v/|v| = < 1 , 0 >
luego, como la función es difeenciable en el punto en estudio (y en todo R2 como ya hemos consignado), puedes plantear para la expresión de su derivada direccional:
Dvg(1/2,0) = ∇g(1/2,0) • V = < -4 , -1 > • < 1 , 0 >,
resuelves el producto escalar, y queda:
Dvg(1/2,0) = -4*1 + (-1)*0 = -4 + 0 = -4.
d)
Observa que el vector gradiente evaluado en el punto en estudio indica la dirección de máximo aumento de la función toxicidas, por lo que tienes que el insecto debe desplazarse en la dirección opuesta, por lo que el vector dirección correspondiente queda expresado:
u = -∇g(1/2,0) = -< -4 , -1 > = < 4 , 1 >, cuyo módulo es: |u| = √(42+12) = √(17),
y su vector unitario asociado queda expresado:
U = u/|u| = ( 1/√(17) )*< 4 , 1 > = < 4/√(17) , 1/√(17) >.
e)
Tienes que el insecto se desplaza según una trayectoria que es una circunferencia, cuya ecuación es:
x2 + y2 = 1/4,
que es una curva de nivel de la función diferenciable en R2: h(x,y) = x2 + y2,
cuyo vector gradiente queda expresado: ∇h(x,y) = < 2x , 2y >.
Luego, tienes todas las condiciones para plantear el Método de los Multiplicadores de Lagrange (observa que indicamos con λ al multiplicador):
∇g(x,y) = λ*∇h(x,y),
x2 + y2 = 1/4,
λ ∈ R;
descompones la ecuación vectorial según las componentes de los vectores gradientes, y queda:
-8x*e1-4x^2-y = 2λx (1),
-e1-4x^2-y = 2λy (2),
x2 + y2 = 1/4 (3);
restas 2λx en ambos miembros de la ecuación señalada (1), y queda:
-8x*e1-4x^2-y - 2λx = 0,
extraes factores comunes en el primer miembro, y queda:
-2x*(4e1-4x^2-y + λ) = 0,
divides por -2 en ambos miembros, y queda:
x*(4e1-4x^2-y + λ) = 0;
luego, por anulación de un producto, tienes dos opciones:
a)
x = 0, que al sustituir en las ecuaciones señaladas (2) (3) queda:
-e1-y = 2λy,
y2 = 1/4,
luego, a partir de la segunda ecuación, tienes dos opciones:
a1)
y = -1/2, reemplazas en la primera ecuación, y queda:
-e3/2 = -λ, multiplicas en ambos miembros por -1, y queda: e3/2 = λ;
por lo que tienes el punto crítico: A1(0,-1/2), con su multiplicador: λ = e3/2;
a2)
y = 1/2, reemplazas en la primera ecuación, y queda:
-e3/2 = λ;
por lo que tienes el punto crítico: A2(0,1/2), con su multiplicador: λ = -e3/2;
b)
4e1-4x^2-y + λ = 0, restas 4e1-4x^2-y en ambos miembros, y queda:
λ = -4e1-4x^2-y (4);
luego, sustituyes en las ecuaciones señaladas (2) (3) (en realidad, solo en la primera de ellas), y queda:
-e1-4x^2-y = -8y*e1-4x^2-y (5),
x2 + y2 = 1/4 (3);
divides en ambos miembros de la ecuación señalada (5) por -e1-4x^2-y (observa que es una expresión que toma valores distintos de cero), y queda:
1 = 8y, divides por 8 en ambos miembros, y queda:
1/8 = y, que al reemplazar en la ecuación señalada (3), y queda:
x2 + 1/64 = 1/4, restas 1/64 en ambos miembros, y queda:
x2 = 15/64, extraes raíz cuadrada en ambos miembros, y tienes dos opciones:
b1)
x = -√(15)/8, reemplazas valores en la ecuación señalada (4), y queda:
λ = -4e-1/16;
por lo que tienes el punto crítico: B1(-√(15)/8,1/8), con su multiplicador: λ = -4e-1/16;
b2)
x = √(15)/8, reemplazas valores en la ecuación señalada (4), y queda:
λ = -4e-1/16;
por lo que tienes el punto crítico: B2(√(15)/8,1/8), con su multiplicador: λ = -4e-1/16;
luego, evalúas la expresión de la función para los cuatro puntos críticos, y queda:
g(0,-1/2) = e3/2 ≅ 4,482,
g(0,1/2) = e1/2 ≅ 1,649,
g(-√(15)/8,1/8) = e-3/16 ≅ 0,829,
g(√(15)/8,1/8) = e-3/16 ≅ 0,829;
luego, tienes que la función alcanza un Máximo absoluto en el punto: A1(0,-1/2), y tienes que la función
alcanza Mínimos Absolutos en los puntos: B1(-√(15)/8,1/8) y B2(√(15)/8,1/8).
Queda que hagas las gráficas correspondientes.
Espero haberte ayudado.
-
Hola !! Una pregunta, este ejercicio de geometría esta resuelto mediante un determinante que contiene el vector normal del plano y de la recta r, se puede hacer tambien sacando un vector de r y a continuación multiplicarlo con el vector del plano de manera que debería dar distinto de 0 ?? Gracias !!
-
Gabriel y el máximo relativo y el mínimo relativo, máximo absoluto y mínimo absoluto?.-
Gracias de nuevo.
-
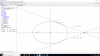
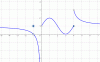
Hola Alguien me podría ayudar a encontrar los tipos de discontinuidades si las hubiera, y el supremo y el ínfimo. Gracias adjunto gráfica.
Gabriel
el 27/5/18En x=-1, discontinuidad de salto finito y evitable.
En x=0, discontinuidad de salto infinito
En x=4, discontinuidad de salto finito y no evitable.
El supremo, entiendo que sea el máximo, que en este caso sería para x=4
El ínfimo, entiendo que sea el mínimo, que en este caso no existe porque la función tiende a menos infinito.