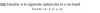Tienes la ecuación matricial:

A*B^t + 2*X = I, restas A*B^t en ambos miembros, y queda:

2*X = I - A*B^t, multiplicas por 1/2 en todos los términos de la ecuación, y queda:

X = (1/2)*I - (1/2)*A*B^t.

Luego, debes hacer las operaciones con las matrices I, A y B, que seguramente tienes como datos en tu enunciado.

Espero haberte ayudado.

Antonio,

¿como lo ves así?

A^1*A*B^t = A^1-I

B^t + 2X = A^1

2X=A^1-B^t

X= (A^1-B^t) dividido por 2.

No tengo valores de las matrices.

Quizás pueda dividir por 

No están bien aplicadas las propiedades de las matrices 

https://www.vitutor.com/algebra/matrices/res.html

Debes tener en cuenta que en las ecuaciones matriciales se aplica primero la propiedad uniforme de la suma o la resta, a fin de pasar términos.

Luego, observa que no es necesario aplicar  la propiedad uniforme de la multiplicación, porque en este caso tienes a la matriz incógnita X  multiplicada por un número.

Luego, si la matriz incógnita X estuviese multiplicada por una matriz invertible A, ahí sí deberías aplicar la propiedad uniforme de la multiplicación de matrices, y multiplicarías por la matriz inversa de la matriz A en ambos miembros.

Espero haberte ayudado.

Ecuación recta tangente 02

sigo sin entender el ejercicio

Tienes que el punto A(2,2) pertenece a la gráfica de la función, por lo que puedes plantear:

f(2) = 2, sustituyes la expresión evaluada de la función en el primer miembro, y queda:

8 + 4*a + 2*b + 1 = 2, restas 9 en ambos miembros, y queda:

4*a + 2*b = -7 (1).

Luego, planteas las expresiones de las funciones derivadas primera y segunda de la función, y quedan:

f ' (x) = 3*x² + 2*a*x + b (2),

f ' ' (x) = 6*x + 2*a (3).

Luego, planteas la condición de posible inflexión en x = 0, y tienes la ecuación:

f ' ' (0) = 0, sustituyes la expresión evaluada de la función derivada segunda en el primer miembro y queda:

2*a = 0, divides por 2 en ambos miembros, y queda:

a = 0.

Luego, reemplazas el valor remarcado en la ecuación señalada (1), cancelas el término nulo, y queda:

2*b = -7, divides por 2 en ambos miembros, y queda:

b = -7/2.

Luego, reemplazas los valores remarcados en la expresión de la función, y en las expresiones señaladas (2) (3), cancelas términos nulos, y quedan:

f(x) = x³ - (7/2)*x + 1,

f ' (x) = 3*x² - 7/2,,

f ' ' () = 6*x.

Luego, evalúas en la expresión de la función para la abscisa del punto de inflexión, y queda: 

f(0) = 1, que es el valor de la ordenada del punto de inflexión, que queda expresado: B(0,1).

Luego, evalúas en la expresión de la función derivada primera para la abscisa del punto de inflexión, y queda:

f ' (0) = -7/2, que es el valor de la pendiente de la recta tangente en el punto de inflexión, que queda planteada: m_T = -7/2.

Luego, con el valor de la pendiente y las coordenadas del punto de inflexión, puedes plantear la ecuación punto-pendiente de la recta tangente, y queda:

y - 1 = -(7/2)*(x - 0), cancelas el término nulo en el agrupamiento, sumas 1 en ambos miembros, y queda:

y = -(7/2)*x + 1, que es la ecuación cartesiana explícita de la recta tangente a la gráfica de la función en su punto de inflexión.

Espero haberte ayudado.

La función es continua en toda la recta real salvo en x=1, donde, necesariamente, no es derivable.

La función tampoco es derivable en x=0.

En el resto de valores reales, lo es.

CONTINUIDAD DE LA FUNCIÓN f(x)

Intervalo (-inf, 0)  -------->  Es continua porque g(x)=e^-x lo es en todo ℛ (y por extensión lo es en el propio intervalo)

Intervalo (0,1)  ------------> Es continua porque h(x)=1-x² lo es en todo ℛ (y por extensión lo es en el propio intervalo)

Intervalo (1,inf)  --------->  Es continua porque i(x)=2/(x-1) lo es en (-inf,1) U (1,inf) (y por extensión lo es en el propio intervalo)

PTO/S CORTE EJE X ------->   En el/ellos siempre se cumple que y=0 

y= -x²+4

Condición y=0 

0= -x²+4  

x²=4

x=√4

x₁=2

x₂= -2

Entonces los puntos de corte con el eje X son dos:

P₁=(2,0)

P₂=(-2,0)

No lo es, pues la expresión no es lineal (de primer grado) y homogénea, al haber una coordenada al cuadrado. Por ello no es expresable como producto de una matriz real  2x3 por el vector columna (x y z).

Llamas x al número de camarotes de 1 plaza, e y al número de camarotes de 2 plazas, por lo tanto x+y=215

Por otro lado en los camarotes de una plaza hay una cama y en los de dos plazas dos camas, por lo tanto x+2y=359

Ya tienes un sistema de ecuaciones con dos incógnitas, que puedes resolver por igualación, sustitución o reducción. 

Si despejo x en la primera ecuación tengo x=215-y. 

Ahora sustituyo esta x en la segunda ecuación y queda 215-y + 2y = 359 ; y= 359-215 ; y=144

Vuelvo a la primera ecuación y cambio el valor de y por 144--> x=215 - 144 ; y=71

por lo tanto hay 71 camarotes de una plaza y 144 de dos plazas.

Espero que lo entiendas :-)

Vamos con una orientación.

Tienes el argumento del límite en tu tercera línea, del que escribimos su numerador y su denominador por separado, y observa que debes corregir:

N = ax² + x - bx² - 3x = (a - b)x² - 2x;

D = √(ax² + x) + √(bx² + 3x).

Luego, observa que para que al dividir por x en el numerador y por su expresión equivalente  √((x²) en el denominador, para se salve la indeterminación debe cumplirse la condición:

a = b (1);

luego, tienes que el numerador y el denominador quedan:

N = 0x² - 2x = -2x, y al dividir por x queda: -2;

D = √(ax² + x) + √(bx² + 3x), y al dividir por √((x²) queda: √(a + 1/x) + √(b + 3/x)

Luego resuelves el límite, y observa que el numerador tiende a -2 y que el denominador tiende a √(a) + √(b),

por lo que el límite de tu enunciado queda: -2/( √(a) + √(b), ), por lo que puedes plantear la ecuación:

-2/( √(a) + √(b) ) = - √(2)/2.

Luego, multiplicas en ambos miembros de la ecuación por -2( √(a) + √(b), y queda:

4 = √(2)( √(a) + √(b) ) (2);

luego, sustituyes la expresión señalada (1) en la ecuación señalada (2), y queda:

4 = √(2)( 2√(b) ),

elevas al cuadrado en ambos miembros, y queda:

16 = 8b, divides por 8 en ambos miembros, y queda:

2 = b;

luego, reemplazas en la ecuación señalada (1), y queda:

a = 2.

Espero haberte ayudado.