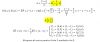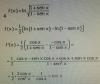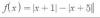-
He acertado 9 de 10 en el exámen de la web sobre ecuaciones de primer grado de 1º de eso y me estoy comiendo la cabeza con la única que he fallado; es esta:
5x-3(2x-1)-(x+5)=1-2(3x+5)
Da 7/4 pero a mí me da 4/1 :\
-
hola alguien me podría explicar en la tercera linea de este ejercicio que formula utiliza y como sale ese resultado??? Gracias

Ángel
el 14/4/18La derivada del logaritmo neperiano de una función es la derivada de la función partido de la función, es decir:
y=lnf
y´=f´/f
Entonces si tenemos
y=ln(1+senx) , su derivada sería y´=(1+senx)´/(1+senx) = (0+cosx)/(1+senx) = cosx/(1+senx)
si tenemos
y=ln(1-senx) , su derivada sería y´=(1-senx)´/(1-senx) = (0-cosx)/(1-senx) = -cosx/(1-senx)
Combinando ambas derivadas ya lo tienes.
-

Ángel
el 14/4/18La función valor absoluto es continua.
Veamos si las funciones dentro de los valores absolutos también lo son, o si por el contrario hay alguna restricción y por tanto una discontinuidad o "no definición de la propia función:
x+1 es una función lineal, que por definición es continua en todo su dominio
x+5 es una función lineal, que por definición es continua en todo su dominio
Por lo tanto tenemos una resta de funciones continuas y por concluimos que f(x) es continua.
-
hola, por favor, alguien me podría ayudar a resolver esta ecuación? x2 -1/3+1=17x2/24
Muchas gracias

Ángel
el 14/4/18x2- 1/(3+1) = 17x2/24
Sumas 3+1 en el denominador y queda:
x2- 1/4 = 17x2/24
Pasas a común denominador:
24x2/24- 6/24 = 17x2/24
Multiplicamos por 24 a cada miembro y queda:
24x2 - 6 = 17x2
Agrupamos términos semejantes y obtenemos:
24x2 - 17x2 = 6
Restamos:
7x2 = 6
Pasamos el factor 7 como divisor al otro lado:
x2 = 6/7
Extraemos raíces y obtenemos las soluciones:
x1= √(6/7)
x2= -√(6/7)

Ángel
el 14/4/18(x2-1)/3 +1 = (17x2)/24
Pasas a común denominador:
8*(x2-1)/24 +24/24 = (17x2)/24
Multiplicamos por 24 a cada miembro y queda:
8*(x2-1) +24 = 17x2
Multiplicamos el paréntesis por 8:
8x2-8 +24 = 17x2
Agrupamos términos semejantes y obtenemos:
-8 +24 = 17x2-8x2
Sumamos y restamos y queda:
16=9x2
Pasamos el factor 9 como divisor al otro lado:
x2 = 16/9
Extraemos raíces y obtenemos las soluciones:
x1= √(16/9) = 4/3
x2= -√(16/9) = -4/3
-
Buenas tardes,
Una pregunta de estadística.
Qué valor deja una probabilidad de 0,90707 de quedar por debajo en una distribución normal.
Muchas gracias,
-
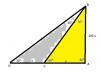
Calcula x e y en la siguiente figura.
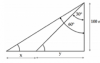 Calcula
x e y en la siguiente figura. (Alguien que me ayude a resolver porfavor!!!)
Calcula
x e y en la siguiente figura. (Alguien que me ayude a resolver porfavor!!!)

Antonio Silvio Palmitano
el 14/4/18Observa que hemos completado las medidas de los ángulos interiores del triángulo rectángulo amarillo, y que hemos hecho lo propio con los ángulos interiores agudos del triángulo oblicuo sombrado con gris (disculpa la falla en el sombreado.
Luego, puedes plantear para el triángulo rectángulo CAB, sombreado en amarillo:
tan(60°) = 100/y, multiplicas por y en ambos miembros, y queda:
tan(60°)*y = 100, divides por tan(60°) en ambos miembros, y queda:
y = 100/tan(60°), reemplazas el valor de la tangente de 60°, y queda:
y = 100/√(3) u ≅ 57,735 u.
Luego, puedes plantear para el triángulo rectángulo DAB, que incluye a toda la figura con ambos sombreados:
tan(30°) = 100/(x + y), multiplicas por (x + y) en ambos miembros, y queda:
tan(30°)*(x + y) = 100, reemplazas el valor de la tangente de 30°, y queda:
( 1/√(3) )*(x + y) = 100, multiplicas por √(3), y queda:
x + y = 100*√(3), restas y en ambos miembros, y queda:
x = 100*√(3) - y, reemplazas el valor remarcado, y queda:
x = 100*√(3) - 100/√(3), extraes denominador común, y queda:
x = (300 - 100)/√(3), resuelves el numerador, y queda:
x = 200/√(3) u ≅ 115,470 u.
Espero haberte ayudado.
-

Ángel
el 14/4/18secα=(3√2)/2
¿ senα ?
¿ cosα ?
¿ tanα ?
secα= (3√2)/2 = 1/(cosα) ----------------> cosα = 1/((3√2)/2) = 2/(3√2) = (2√2)/(3√2√2) = (2√2)/(3*2) = (√2)/3
cos2α+sen2α = 1 -----------> ((√2)/3)2+sen2α = 1 ---------> 2/9 + sen2α = 1 ------> sen2α =7/9 --------> senα =(√7)/3
tanα = (senα)/(cosα) = ((√7)/3/((√2)/3) = (√7)/√2 = (√7√2)/(√2√2) = (√7√2)/2 = (√14)/2


Antonio Silvio Palmitano
el 14/4/18Recuerda la identidad trigonométrica:
secα = 1/cosα, reemplazas el valor de la secante en el primer miembro, y queda:
3*√(2)/2 = 1/cosα, multiplicas por √(2)*cosα en ambos miembros, y queda:
3*cosα = √(2), divides por 3 en ambos miembros, y queda:
cosα = √(2)/3.
Recuerda la identidad trigonométrica:
sen2α + cos2α = 1, reemplazas el valor del coseno en el primer miembro, y queda:
sen2α + ( √(2)/3 )2 = 1, resuelves el segundo término, y queda:
sen2α + 2/9 = 1, restas 2/9 en ambos miembros, y queda:
sen2α = 7/9, extraes raíz cuadrada en ambos miembros (observa que elegimos la raíz positiva porque el ángulo es agudo), y queda:
senα = √(7)/3.
Recuerda la identidad trigonométrica:
tanα = senα/cosα, reemplazas los valores remarcados, simplificas, y queda:
tanα = √(7)/√(2), multiplicas al numerador y al denominador del segundo miembro por √(2), y queda.
tanα = √(7)* √(2)/2, asocias las raíces en el numerador del segundo miembro, y queda:
tanα = √(14)/2.
Espero haberte ayudado.