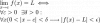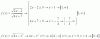¿Me ayudarían a resolver este límite sin L'hôpital?

Hola, me podriais ayudar con el crecimiento y decrecimiento de esta función?

f(x)= 3x²+3 

     ____________

              x

hola, mi porofe no ha sabido decirme :(

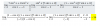
Que vale   lim_{x→ - ∞} x^x   ?????

como demuestro por la definición formal de limite que lim(x->c)(x³)=c³

Hola!

Estaría bien planteado este ejercicio??? Gracias

Hola.

Queria saber si me podian ayudar con este ejercicio de transformaciones lineales.

El ejercicio me dice que Q es una transformacion que va de R4 a R4, me dicen que es un isomorfismo. y me  pide hallar la inversa de esa transformacion lineal y me dan los siguientes datos:

Q (0,2,2,1) = (1,0,0,0)

Q(1,3,-1,0) = (0,1,0,0)

Q(2,1,0,0) = (0,0,1,0)

Q(0,1,1,3) = (0,0,0,1)

Luego de muchos calculos, pude hallar la transformacion lineal asociada que me quedo.

Q(x,y,z,w)  = ( -3/35 x + 6/35 y + 3/7 z - 1/5 w  , -1/7 x + 2/7 y - 2/7 z , 4/7 x - 1/7 y + 1/7 z , 1/35 x - 2/35 y - 1/7 z + 2/5 w)

Ahora el problema es que tengo que hallar la inversa...y por el metodo que estoy utilizando, que consiste en utilizar nuevos valores a,b,c,d y que todos estos terminos de la transformacion  me quede en funcion de a,b,cd...no estoy consiguiendo resultados, son calculos interminables y queria saber si habia una manera mas facil de hacerlo o mas simple.

Por determinantes, tendria que hallar la matriz asociada y luego el cofactor de cada uno de los elementos para luego dividirlo por determinante ,etc...Tambien es larguisimo..

Por eso mi pregunta va dirigida a que si no hay algo que se me esta escapando, porque es un ejercicio de parcial y los parciales no duran tanto y con este ejercicio ya voy horas.

Hola!,

Les traigo una consulta ya que lo repense muchas veces y no he conseguido terminar de resolverlo, me dan la formula de un plano que dice TT=-x+2y+z=4 . Hallar los vertices de un triangulo rectangulo que pertenezca al plano.

Lo que plantee fue dar valores a x e y  al plano y sacar z de la formula del plano, encontrando asi 2 puntos para construir una recta, la cual luego con su vector director mediante el producto punto hallo un vector director que me cumpla que usando el producto punto de 0 y garantizar que sean perpendiculares.

Luego me pierdo en razonamientos pero estoy perdiendo de vista los puntos y no se si voy bien y como continuar para cerrar el triangulo. Por favor si me pueden hechar un poco de luz mas que agradecida.

Saludos cordiales y gracias por su tiempo!

transcribo mis resoluciones

TT:-x+2y+z=4

Calculo punto A, doy valores a X e Y averiguo Z
x=0
Y=1
z=? 
-x+2y+z=4
-0+2.1+z=4
z=2

A=(0,1,2)

Punto B
x=1
y=0
z=?
-x+2y+z=4

-1+2.0+z=4
z=5
B=(1,0,5)

AB(vector)=(1,0,5)-(0,12)=(1,-1,3)
Recta 1= α(1,-1,3)+(0,1,2)

Como debe ser perpendicular una recta que corte a esta en 90º el producto punto debe dar 0
Doy valores al vector director de la 2da recta y averiguo cuando cumple que de 0
x=1,
y=1,

(1,-1,3).(1,1,x)=0

1-1+3x=0
x=0

[1 BACH]: ¿Por qué en el teorema del seno tenemos dos soluciones? ¿De donde salen? 
En mi clase, mi profesor lo hace así, con dos soluciones, y no se de dónde salen.

me podrían ayudar , como quedaría la negación de 

Hola , tengo un problema no puedo resolver esto y m’en gustaria que me ayudaras o explicarás gracias