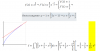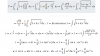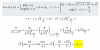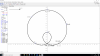
Has planteado correctamente el sistema de ecuaciones del Método de los Multiplicadores de Lagrange, que te ha quedado (observa que ordenamos y agrupamos términos con factor común en tus dos primeras ecuaciones, y que operamos en la última ecuación):

3(x² + y²) - 6xy - 2λx = 0,

-3(x² + y²) + 6xy - 2λy = 0,

x² + y² = 1.

Luego, reemplazas el valor del segundo miembro de la tercera ecuación en las dos primeras, mantienes la tercera ecuación, y queda:

3 - 6xy - 2λx = 0,

-3 + 6xy - 2λy = 0,

x² + y² = 1.

Multiplicas por -1 en todos los términos de la primera ecuación, haces pasajes de términos en las dos primeras ecuaciones, y queda:

6xy + 2λx = 3,

6xy - 2λy = 3,

x² + y² = 1.

Sustituyes la primera ecuación por la resta entre ella y la segunda ecuación, mantienes las dos últimas ecuaciones, y queda:

2λx + 2λy = 0,

6xy - 2λy = 3,

x² + y² = 1.

Divides por 2 en todos los términos, y extraes factor común, en la primera ecuación, y queda:

λ(x + y) = 0,

6xy - 2λy = 3,

x² + y² = 1.

Luego, por anulación de un producto en la primera ecuación, tienes dos opciones:

1)

λ = 0, reemplazas, y el sistema queda:

6xy = 3, de aquí despejas: y = 1/(2x) (1),

x² + y² = 1;

luego, reemplazas la expresión señalada (1) en la segunda ecuación, y queda:

x² + 1/4x² = 1, multiplicas en todos los términos por 4x², haces pasaje de término, y queda:

4x⁴ - 4x² + 1 = 0, factorizas el primer miembro, y queda:

(2x² - 1)² = 0, haces pasaje de potencia como raíz, y queda:

2x² - 1 = 0, haces pasaje de término, luego de factor como divisor, y queda:

x² = 1/2, aquí haces pasaje de potencia como raíz, y tienes dos opciones:

1a)

x = -1/√(2), reemplazas en la ecuación señalada (1), resuelves, y queda: y = -1/√(2),

y tienes el punto crítico: A₁( -1/√(2) , -1/√(2) );

1b)

x = 1/√(2), reemplazas en la ecuación señalada (1), resuelves, y queda: y = 1/√(2),

y tienes el punto crítico: B₁( 1/√(2) , 1/√(2) );

2)

x + y = 0, aquí haces pasaje de término y queda: y = -x (2);

luego, sustituyes y el sistema queda:

-6x² + 2λx = 3 (3),

2x² = 1, aquí haces pasaje de factor como divisor, y luego de potencia como raíz, y tienes dos opciones:

2a)

x = -1/√(2), reemplazas en la ecuación señalada (2), resuelves, y queda: y = 1/√(2);

luego reemplazas en la ecuación señalada (3) y puedes despejar: λ = -3√(2),

y tienes el punto crítico: A₂( -1/√(2) , 1/√(2) );

2b)

x = 1/√(2), reemplazas en la ecuación señalada (2), resuelves, y queda: y = -1/√(2),

luego reemplazas en la ecuación señalada (3) y puedes despejar: λ = 3√(2),

y tienes el punto crítico: B₂( 1/√(2) , -1/√(2) ).

Luego, solo queda que evalúes la expresión para cada uno de los puntos críticos, para decidir en cuál (o cuáles) de ellos es que la función alcanza su valor Máximo Absoluto y su valor Mínimo Absoluto.

Espero haberte ayudado.

si no recuerdo mal, λ nunca puede valer 0 porque no nos aporta ningún punto crítico. Por el resto ya supe por donde tirar, ahora mirando en el plano tangente me he vuelto a atascar :(

Observa que la función a optimizar y la función de restricción son ambas continuas y también diferenciables en R³.

Observa que la ecuación de restricción corresponde a una circunferencia, que es una curva de R² que es cerrada y acotada.

Recuerda además que si el multiplicador es distinto de cero tienes que corresponde a un extremo absoluto, pero si el multiplicador es igual a cero, como ocurre con dos de los puntos críticos de tu ejercicio, no tienes asegurado que se trate de un extremo, por lo que de igual forma debes incluirlo en tu estudio de la función con restricción.

Espero haberte ayudado.

¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

A ver si te sirve

Ecuación: r = 1 + 2*sen(φ), en el dominio: [ 0 , 2π ].

Esta es la gráfica en coordenadas polares (φ.r), que hemos obtenido a partir de un graficador en línea, y como puedes ver, no es una gráfica simple, porque la curva se corta consigo misma en el polo (origen), y si haces el intento de pasar a coordenadas cartesianas, verás que obtendrás una ecuación con la que es muy complicado tratar.

Luego, a fin de determinar el dominio que corresponde al rulo interior, puedes apelar a una tabla de valores, lo haces, y verás que corresponde al intervalo: [ 7π/6 , 11π/6 ], y que para el rulo exterior tienes que corresponde el intervalo complementario.

Luego, planteas la expresión del área limitada por una curva, expresada en coordenadas polares, y tienes:

A = (1/2) * _a∫^b ( r(φ) )²*dφ;

luego, sustituyes los valores de los límites de integración y la expresión de la función, y queda:

A = (1/2) * _7π/6∫^11π/6 ( 1+2*sen(φ) )²*dφ;

luego, desarrollas el cuadrado en el argumento de la integral, y queda:

A = (1/2) * _7π/6∫^11π/6 ( 1 + 4*sen(φ) + 4*sen²(φ) )*dφ;

luego, aplicas la identidad del cuadrado del seno de un ángulo en función de su coseno en el último término del argumento, y queda:

A = (1/2) * _7π/6∫^11π/6 ( 1 + 4*sen(φ) + 4*( (1-cos(2φ) )/2 ) )*dφ;

simplificas y distribuyes en el último término del argumento de la integral, y queda:

A = (1/2) * _7π/6∫^11π/6 ( 1 + 4*sen(φ) + 2 - 2*cos(2φ) )*dφ;

reduces términos semejantes en el argumento de la integral, y queda:

A = (1/2) * _7π/6∫^11π/6 ( 3 + 4*sen(φ) - 2*cos(2φ) )*dφ;

resuelves la integral (observa que indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:

A = (1/2) * [ 3*φ - 4*cos(φ) - sen(2φ) ], para evaluar en el intervalo: [ 7π/6 , 11π/6 ];

luego, evalúas, y queda:

A = (1/2)*[ (11π/2 - 2*√(3) + √(3)/2) ) - (7π/2 + 2*√(3) - √(3)/2) ];

distribuyes en el agrupamiento, reduces términos semejantes, y queda:

A = (1/2) * [ 2π - 3*√(3) ] = π - 3*√(3)/2 ≅ 0,5435.

Espero haberte ayudado.

Recuerda el Teorema del Resto que has visto en clase.

Observa que tienes que -1 es raíz, por lo que el resto al dividir el polinomio por (x+1) es igual a 0;

luego, aplicas el teorema, y puedes plantear:

P(-1) = 0, sustituyes en el primer miembro la expresión del polinomio evaluado, y queda:

2(-1)³ - 5(-1)² + a(-1) + b = 0, resuelves términos, reduces términos semejantes, haces pasaje de término, y queda:

-a + b = 7, aquí haces pasaje de término, y queda: b = 7 + a (1).

Observa que tienes que el resto al dividir el polinomio por (x+2) es igual a b;

luego, aplicas el teorema, y puedes plantear:

P(-2) = b, sustituyes en el primer miembro la expresión del polinomio evaluado, y queda:

2(-2)³ - 5(-2)² + a(-2) + b = b, resuelves términos, reduces términos semejantes, haces pasaje de término, y queda:

-2a = 36, aquí haces pasaje de factor como divisor, y queda: a = -18;

luego, reemplazas el valor remarcado en la ecuación señalada (1) y queda: b = 7 - 18 = -11.

Luego, la expresión del polinomio qeuda:

P(x) = 2x³ - 5x² - 18x - 11.

Espero haberte ayudado.

Hola! Muchas gracias, se entiende bien :)

Pero me queda una duda, No faltaría sumar 1/3 ? que es donde la recta corta al eje OY.

Saludos!

¡Oh, cielos, sí, me olvidé del segmento fácil!

Tomo nota. Prometido

Mándanos las indicaciones que te ha dado tu profesor y te ayudamos.

No estoy muy segura de qué es lo que quieres decir, de modo que aquí te envío un ejemplo resuelto y explicado paso a paso:

Teniendo esta inecuacion: x²-5x-3<0 Te pregunta qué intervalo será negativo

La "cambiamos" a una igualdad: x²-5x+6=0

Haces la ecuación de segundo grado aplicando su fórmula: X= 5±√25-24 /2 = 5±1/2 = 3 y 2

Los aplicas a la recta real y "pones" cualquier número que esté a la izquierda del dos como x y haces la comprobación. Yo he escogido el 1 : 1-5+6= 2

Ahora, aplica cualquier número que esté a la izquierda del 3, Yo he cogido el 10: 10²-50+6= 100-50+6=56

Fíjate que el símbolo de ambos es positivo, así pues, los intervalos (-∞,2) y (3,∞) serán positivo

Realiza lo mismo que antes (aplicar un número) pero este caso debe estar entre los números 2 y 3, si lo realizas, verás que este es el intervalo negativo. Recuerda que los números 2 y 3 no están oncluidos en este intervalo (2, 3)

Aquí abajo te envío otro, lo que tienes que hacer es resolver la inecuación: -4x²+x-3 ≥ 0. Este es más complicado que el de antes.

Espero que te haya resultado de ayuda y disculpa si no está muy bien explicado, si lo deseas, te puedo dar la solución de esta última inecuación para que la compruebes

Puedes comenzar por dibujar un triángulo ABC, en el que la base es AB, cuya longitud es:

|AB| = 1000 Km.

Luego, coloca a los observadores en los vértices A y B, y al objeto luminoso en el vértice C.

Luego, observa que tienes las medidas de los tres ángulos interiores del triángulo:

α = 85° (en el vértice A), 

β = 87° (en el vértice B),

γ = 180° - 85° - 87° = 8° (en el vértice C.

Luego, puedes plantear el Teorema del Seno:

a)

senβ/|AC| = senγ/|AB|, reemplazas valores, y queda:

sen(87°)/|AC| = sen(8°)/1000, de aquí despejas:

|AC| =1000*sen(87°)/sen(8°) ≅ 7175,449 Km,

que es la distancia del primer observador al objeto luminoso;

b)

senα/|BC| = senγ/|AB|, reemplazas valores, y queda:

sen(85°)/|BC| = sen(8°)/1000, de aquí despejas:

|BC| =1000*sen(85°)/sen(8°) ≅ 7157,954 Km,

que es la distancia del segundo observador al objeto luminoso.

Luego, observa que las distancias son muy pequeñas como para corresponder a una estrella.

Espero haberte ayudado.

Y pensar que era tan fácil como eso...¡Muchas gracias!