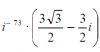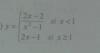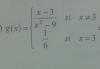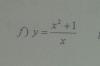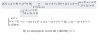
Para comenzar, considera el primer factor por separado.

i^-73 = i^-76+3 = i^-76*i³ = i^4*(-19)*i³ = (i⁴)¹⁹*i³ = 1¹⁹*(-i) = 1*(-i) = -i.

Luego, sustituyes, y la expresión de tu enunciado queda:

z = -i*( 3*√(3)/2 - 3*i/2 ) = distribuyes = - 3*√(3)*i/2 + 3*i²/2 =

=  - 3*√(3)*i/2 + 3*(-1)/2 = - 3*√(3)*i/2 + 3*(-1)/2 = - 3*√(3)*i/2 - 3/2 = -3/2 - 3*√(3)*i/2;

y observa que tienes un número complejo cuyo punto representativo perteneciente al tercer cuadrante;

luego, planteas su módulo y su argumento:

|z| = √( (-3/2)² + ( -3*√(3)/2 )² ) = √( 9/4 + 27/4 ) = √(36/4) = √(9) = 3;

tanθ = ( -3*√(3)/2 ) / (-3/2) = √(3), compones con la función inversa de la tangente, y queda: 

θ = π/3 + π = 4π/3 rad;

luego, el número complejo queda expresado en forma polar:

z = |z|_θ = 3_4π/3.

Espero haberte ayudado.

Observa que puedes expresar al argumento del logaritmo en forma fraccionaria, luego simplificarla, y expresarla como potencia con base 2:

0,25 = 25/100 = simplificas = 1/4 = 1/2² = 2^-2.

Luego, tienes:

log₂(0,25) = reemplazas = log₂(2^-2) = resuelves = -2.

Recuerda: si el argumento del logaritmo es una potencia cuya base es la base del logaritmo, entonces el resultado es el exponente de la potencia que tienes como argumento.

Espero haberte ayudado.

¡¡Muchas gracias!!

Observa que el dominio de la función es: D = R - {-1} (observa que la expresión de la función se indetermina para x = -1).

Luego, observa que puedes simplificar la expresión fraccionaria que tienes en tu enunciado:

(2x-2)/(x2-1) = 2*(x-1) / (x-1)*(x+1) = simplificas = 2/(x+1).

Luego, la expresión de la función a trozos que da expresada:

g(x) =

2/(x+1)                     si x < 1 y x ≠ -1,

2*x-1                        si x ≥ 1.

Luego, plantea el estudio de la continuidad de la función en los dos puntos notables, que son: x = -1 que no pertenece al dominio de la función, y x = 1 que si pertenece al dominio, pero es un punto de corte en la expresión de la función.

a)

Para x = -1:

1°)

g(-1) no está definida;

2°)

Lím(x→-1-) g(x) = Lím(x→-1-) 2/(x+1) = -∞ (observa que el denominador tiende a cero desde valores negativos),

Lím(x→-1+) g(x) = Lím(x→-1+) 2/(x+1) = +∞ (observa que el denominador tiende a cero desde valores positivos);

3°)

tienes que la gráfica de la función presenta asíntota vertical cuya ecuación es: x = -1,

por lo que es discontinua esencial (o inevitable) en este punto.

b)

Para x = 1:

1°)

g(1) = 2*1 - 1 = 2 - 1 = 1;

2°)

Lím(x→1-) g(x) = Lím(x→1-) 2/(x+1) = 2/2 = 1,

Lím(x→1+) g(x) = Lím(x→1+) 2*x - 1 = 2*1 - 1 =2 - 1 = 1,

luego, como los límites laterales son iguales, tienes:

Lím(x→1) g(x) = 1;

3°)

como tienes: g(1) = Lím(x→1) g(x) = 1,

puedes concluir que la gráfica de la función es continua en x = 1.

Espero haberte ayudado.

Porque hay que hallar el dominio?? No hay que hacer solo cuando x=1 ???

Planteaste correctamente la ecuación de interés compuesto:

C_n = C_i*(1 + i)ⁿ.

Luego, tienes los datos para este problea:

i = 12 % = 0,12, con capitalización anual;

C_i = 50000 euros;

C_n = 2*C_i = 2*50000 = 100000 euros;

n = a determinar (expresado en años);

luego, sustituyes, resuelves el agrupamiento, y queda

100000 = 50000_i*(1,12)ⁿ, haces pasaje de factor como divisor, y queda:

2 = (1,12)ⁿ, compones en ambos miembros con la función logarítmica decimal, y queda:

log(2) = log ( (1,12)ⁿ ), aplicas la propiedad del logaritmo de una potencia en el segundo miembro, y queda:

log(2) = n*log(1,12), haces pasaje de factor como divisor, y queda:

log(2)/log(1,12) = n;

luego, evalúas, y queda:

n ≅ 6,12 años.

Espero haberte ayudado.

Cn = 2*Ci = 2*50000 = 100000 euros;

PORQUE SE MULTIPLICARÍA POR 2, PARA PODER SACAR (Cn ) ESTO ??

1)

Tienes que el dominio de la función es: D_f = R.

Luego, haces pasaje de término, y queda:

y - 1 = 2^x, compones con la función logaritmica en base 2 en ambos miembros, y queda:

log₂(y-1) = x, y observa que debe cumplirse la condición: y > 1,

por lo que la imagen de la función es: I_f = (1,+∞).

Luego, permutas variables en la última ecuación, y queda:

log₂(x-1) = y,

por lo que tienes que el dominio de la función inversa es: D_i = (1,+∞), su imagen es: I_i = R,

y su expresión es: y = log₂(x-1).

2)

Tienes que el dominio de la función es: D_f = (0,+∞).

Luego, haces pasaje de término, y queda:

y - 2 = log₃(x), compones con la función exponencial en base 3 en ambos miembros, y queda:

3^y-2 = x, y observa que está definida para todo valor y real,

por lo que la imagen de la función es: I_f = R.

Luego, permutas variables en la última ecuación, y queda:

3^x-2  = y,

por lo que tienes que el dominio de la función inversa es: D_i = R, su imagen es: I_i = (0,+∞),

y su expresión es: y = 3^x-2.

3)

Tienes que el dominio de la función es: D_f = [0,+∞).

Luego, haces pasajes de términos, y queda:

x² = 4 - y, compones con la función raíz cuadrada positiva en ambos miembros, y queda:

x = √(4-y), y observa que debe cumplirse la condición: y ≤ 4,

por lo que la imagen de la función es: I_f = (-∞,4].

Luego, permutas variables en la última ecuación, y queda:

y = √(4-x),

por lo que tienes que el dominio de la función inversa es: D_i = (-∞,4], su imagen es: I_i = [0,+∞),

y su expresión es: y = √(4-x).

Espero haberte ayudado.

Observa que el dominio de la función es: D = R - {-3} (observa que la expresión de la función se indetermina para x = -3).

Luego, observa que puedes simplificar la expresión fraccionaria que tienes en tu enunciado:

(x-3)/(x²-9) = (x-3) / (x-3)*(x+3) = simplificas = 1/(x+3).

Luego, la expresión de la función a trozos que da expresada:

g(x) =

1/(x+3)                     si x ≠ -3 o x ≠ 3

1/6                            si x = 3.

Luego, plantea el estudio de la continuidad de la función en los dos puntos notables, que son: x = -3 que no pertenece al dominio de la función, y x = 3 que si pertenece al dominio, pero es un punto de corte en la expresión de la función.

a)

Para x = -3:

1°)

g(-3) no está definida;

2°)

Lím(x→-3-) g(x) = Lím(x→-3-) 1/(x+3) = -∞ (observa que el denominador tiende a cero desde valores negativos),

Lím(x→-3+) g(x) = Lím(x→-3+) 1/(x+3) = +∞ (observa que el denominador tiende a cero desde valores positivos);

3°)

tienes que la gráfica de la función presenta asíntota vertical cuya ecuación es: x = -3,

por lo que es discontinua esencial (o inevitable) en este punto.

b)

Para x = 3:

1°)

g(3) = 1/6;

2°)

Lím(x→3) g(x) = Lím(x→3) 1/(x+3) = 1/6; 

3°)

como tienes: g(3) = Lím(x→3) g(x) = 3,

puedes concluir que la gráfica de la función es continua en x = 3.

Espero haberte ayudado.

Me lia cuando en una funcion a trozos aparece que x es igual o no es igual a un numero. Porque hay que hacer el dominio??

Lo primero, x≠0 ya que está en el denominador, por tanto puede haber asíntota vertical en x=0.

Segundo, para que sea una asíntota su límite tiene que ser o ∞ o -∞ para ser asíntota.

Vamos a comprobarlo:

lim x->0⁺ (x²+1)/x. Ve poniendo datos a la x mayores a 0

(0,1²+1)/0,1=10,1

(0,01²+1)/0,01=100,01

(0,001²+1)/0,001=1000,001

(0,0001²+1)/0,0001=10000,0001

Como puedes comprobar, el límite tiende a ∞, haríamos lo mismo por la izquierda.

lim x->0^- (x²+1)/x. Ve poniendo datos a la x menores a 0

((-0,1)²+1)/-0,1=-10,1

((-0,01)²+1)/-0,01=-100,01

((-0,001)²+1)/-0,001=-1000,001

((-0,0001)²+1)/-0,0001=-10000,0001

¿Lo ves? El límite tiende a -∞ por la izquierda.

Sabemos que si hay asíntota oblícua, no hay asíntota horizontal. Vamos a comprobarlo:

(x²+1)/x =x+(1/x); sale una asíntota oblícua en y=x.

Finalmente, hay que representar la función con los datos obtenidos. Saldría algo así:

Espero haberte ayudado.

No lo entiendo muy bien no tendría que ser (a+b+c)(b+c)=0?

(a+b+c)(b+2c)=0 corrijo

Considera los elementos del subconjunto:

p(x) = a + b*x + c*x² (con a, b y c reales, y se cumple: p(1) - p ' (1) = 0, y tienes: p ' (x) = b + 2c*x),

q(x) = A + B*x + C*x² (con A, B y C reales, y se cumple: q(1) - q ' (1) = 0, y tienes: q ' (x) = B + 2C*x);

considera al número real genérico k;

y considera al vector nulo del espacio vectorial V: O(x) = 0 + 0*x + 0*x² = 0 (polinomio nulo).

1°)

Prueba que el subconjunto no es vacío, y para ello puedes probar que el vector nulo del espacio vectorial V pertenece al subconjunto (observa que tienes: O ' (x) = 0):

O(1) - O ' (1) = reemplazas = 0 - 0 = 0,

por lo que tienes que O(x) pertenece al subconjunto.

2°)

Prueba que la suma de dos elementos del subconjunto pertenece al subconjunto:

[ p(1) + q(1) ] - [ p(1) + q(1) ] ' = aplicas la propiedad de la derivada de la suma de funciones polinómicas, y queda:

= p(1) + q(1) - [ p ' (1) + q ' (1) ] = distribuyes el signo en el segundo agrupamiento, y queda:

= p(1) + q(1) - p ' (1) - q ' (1) = ordenas y asocias términos, y queda:

= [ p(1) - p ' (1) ] + [ q(1) - q ' (1) ] = reemplazas valores (observa las ecuaciones remarcadas al comienzo), y queda:

= 0 + 0 = 0,

por lo que tienes que la suma de dos elementos del subconjunto pertenece al subconjunto.

3°)

Prueba que el múltiplo escalar de un elemento del subconjunto pertenece al subconjunto:

k*p(1) - [ k*p(1) ] ' =

extraes el factor constante fuera de la expresión de la función derivada evaluada en el segundo término, y queda:

= k*p(1) - k*p ' (1) = extraes factor común, y queda:

= k*[ p(1) - p ' (1) ] = reemplazas valores (observa las ecuaciones remarcadas al comienzo), y queda:

= k*0 = 0,

por lo que tienes que el múltiplo escalar de un elemento del subconjunto pertenece al subconjunto.

Luego, como has visto en clase, tienes que el subconjunto es un subespacio vectorial de V = R₂(x).

Espero haberte ayudado.

Disculpla. Copié mal (p(1)=p'(1))

Ahora va:

Gracias peor no entiendo muy bien lo que hace a partir del b=-2c, a pesar de que el comentario de arriba comprendio mal el enunciado, no debería seguirse ese proceso para ver que es subespacio?

Gracias de nuevo estos ejercicios no los entiendo muy bien ;/

Observa que para resolverla debes aplicar una sustitución (cambio de variable) y, en principio, cualquiera de las dos expresiones puede ser tomada como principal, pero el objetivo es que una vez hecha la sustitución, la tarea para terminar sea la más sencilla que sea posible.

1°)

Si eliges:

f = senx, de aquí tienes: f ' = cosx;

luego sustituyes, y queda:

I = ∫ sen³x*cosx*dx = ∫ f ' * f³ * dx = ∫ f³ * f ' * dx = resuelves = (1/4) * f⁴ + C = sustituyes = (1/4)*sen⁴x + C.

2°)

Si eliges:

f = cosx, de aquí tienes: f ' = -senx, y luego tienes: -f ' = cosx;

luego sustituyes, y queda:

I = ∫ sen³x*cosx*dx = ∫ sen²x*senx*cosx*dx = aplicas identidad trigonométrica:

= ∫ (1-cos²x)*senx*cosx*dx = sustituyes = ∫ (1-f²)*( -f ' )*f*dx = distribuyes:

= ∫ (-f+f³) * f ' * dx = integras = -(1/2)*f² + (1/4)*f⁴ + D = sustituyes = -(1/2)*cos²x + (1/4)*cos⁴x + D.

Luego, observa que las expresiones son equivalentes:

Partes desde el segundo resultado, extraes factor común, y queda:

I = (1/4)*cos²x*(-2 + cos²x) + D = aplicas identidad trigonométrica:

= (1/4)*(1 - sen²x)*(-2 + 1-sen²x) + D = reduces términos en el último factor:

= (1/4)*(1 - sen²x)*(-1-sen²x) + D = distribuyes los dos últimos factores (oberv que tienes cancelaciones):

= (1/4)*(-1 + sen⁴x) + D = ordenas términos en el agrupamiento:

= (1/4)*(sen⁴x - 1) + D = distribuyes:

= (1/4)*sen⁴x - 1/4 + D = reduces la expresión de la constante arbitraria (sustituyes: -1/4 + D = C):

= (1/4)*sen⁴x + C.

Observa que la primera opción es mucho más sencilla y práctica que la segunda, y también observa que debes tener en cuenta que las identidades trigonométricas permiten cambiar la apariencia de una expresión, como ha ocurrido en este caso, y recuerda que C y D son constantes arbitrarias, por lo que -1/4 + D también lo es.

Espero haberte ayudado.

Foto del enunciado original, por favor.