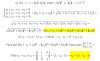Pon foto del enunciado original, por favor.

Por si no se lee bien

a) Enuncia el TVM (Teorema del valor medio/Lagrange)

b) Aplicando el TVM a f(x)=1/x² , probar que sean los números reales 1<a<b, se cumple que a+b<2a²b² 

No pido en realidad la solución, sino una guía de como resolver esos ejercicios, ya que tengo bastantes problemas a la hora de hacerlo.

Estos ejercicios no son fáciles. Analiza el procedimiento:

Vamos con una orientación.

Tienes la inecuación: 1 - 2x > 2x + 4.

Luego, representa gráficamente las rectas (te dejo la tarea):

R: y = 1 - 2x (observa que los puntos (0,1) y (1,-1) pertenecen a la recta R),

S: y = 2x + 4 (observa que los puntos (0,4) y (1,6) pertenecen a la recta S).

Luego, sombrea en el plano el sector para en el que la gráfica de la recta R es más alta que la gráfica de la recta S,

y la solución de la inecuación queda representada por el tramo del eje OX que queda dentro del sombreado.

Observa también que la desigualdad es estricta, por lo que debes considerar que el punto de intersección entre la recta R y la recta S no pertenece a la región sombreada y, por lo tanto, su proyección sobre el eje OX no pertenece al conjunto solución.

Espero haberte ayudado.

Área y Volumen de un poliedro

En la primera integral, ¿Está 4-cos (x) dentro de la raíz? Tal y como lo has puesto cos (x) estaría fuera y sería una integral inmediata, pero si está dentro la cosa cambia. Especifica y te ayudo.

La segunda es muy fácil. Solo tienes que factorizar el denominador y averiguar los valores de A, B y C (por ser de grado 3), siquiendo el método de este vídeo: Integral racional en fracciones simples 01

Inténtalo y cuelga tus resultados aquí, si tienes algo mal ya te oriento mejor.

Vamos con una orientación.

1)

Tienes la integral:

I = ∫ senx*√(4-cosx)*dx,

luego, plantea la sustitución (cambio de variable):

w = 4-cosx, de donde tienes: dw = senx*dx, luego sustituyes, y queda:

I = ∫ √(w)*dw = ∫ w^1/2*dw = (2/3)*w^3/2 + C = (2/3)*(4 - cosx)^3/2 + C.

2)

Tienes la expresión en el argumento de la integral (observa que el grado del numerador es menor que el grado del denominador):

f(x) = (x²+12x+12)/(x³-4x) =

= (x²+12x+12) / x(x-2)(x+2) = a/x + b/(x-2) + c/(x+2) = ( a(x-2)(x+2) + bx(x+2) + cx(x-2) ) / x(x-2)(x+2),

luego igualas los numeradores remarcados (observa que los denominadores son iguales), y queda la igualdad entre polinomios:

a(x-2)(x+2) + bx(x+2) + cx(x-2) = x² + 12x + 12,

luego, como tienes tres coeficiente a determinar, eliges tres valores de x, observa que los más convenientes son 2, -2 y 0, los reemplazas y tienes las ecuaciones:

8b = 40, aquí haces pasaje de factor como divisor, y queda: b = 5,

8c = -8, aquí haces pasaje de factor como divisor, y queda: c = -1,

-4a = 12, aquí haces pasaje de factor como divisor, y queda: a = -3.

Luego, tienes la integral:

I = ∫ ( (x²+12x+12)/(x³-4x) )*dx =

= ∫ (-3/x)*dx + ∫ ( 5/(x-2) )*dx + ∫ ( -1/(x+2) )*dx =

= -3*∫ (1/x)*dx + 5*∫ ( 1/(x-2) )*dx - 1*∫ ( 1/(x+2) )*dx =

= -3*ln|x| + 5*ln|x-2| - ln|x+2| + C.

Espero haberte ayudado.

Recuerda las identidades:

cos²x = 1/(1 + tan²x) (1),

sen²x = tan²x/(1+tan²x) (2),

cos(2x) = cos²x - sen²x (3),

sen(2x) = 2*senx*cosx (4),

tanx = senx/cosx (5).

Tienes: α < 270° y tanα = -3, por lo que tienes que α pertenece al segundo cuadrante (recuerda que la tangente toma valores positivos en el primer cuadrante y en el tercer cuadrante), por lo que tienes que α/2 pertenece al primer cuadrante;

luego, puedes aplicar la sustitución (cambio de incógnita):

x = α/2 (*) (observa que tienes: x < 270°/2 = 135°, y recuerda que x = α/2 pertenece al primer cuadrante);

luego: 

1°)

Aplicas las identidades señaladas (1) (2), y quedan:

cos²x = 1/(1 + tan²x) = 1/(1 + (-3)²) = 1/(1 + 9) = 1/10,

sen²x = tan²x/(1+tan²x) = (-3)2/(1 + (-3)2) = 9/(1 + 9) = 9/10;

luego, haces pasaje de potencia como raíz entre los primeros miembros y los últimos miembros de las cadena de igualdades (observa que elegimos el signo positivo en las raíces), y quedan:

cosx = √(1/10) = 1/√(10),

senx = √(9/10) = 3/√(10).

2°)

Aplicas las identidades señaladas (3) (4) (5), y quedan:

cos(2x) = cos²x - sen²x = ( 1/√(10) )² - ( 3/√(10) )² = 1/10 - 9/10 = -8/10 = -4/5,

sen(2x) = 2*senx*cosx = 2*( 3/√(10) )*( 1/√(10) ) = 6/( √(10) )² = 6/10 = 3/5,

tan(2x) = sen(2x)/cos(2x) = = (3/5) / (-4/5) = -3/4;

luego, sustituyes la expresión señalada (*) en los primeros miembros de las cadenas de igualdades, igualas con los últimos miembros, y queda:

cosα = -4/5,

senα = 3/5,

tanα = -3/4.

Espero haberte ayudado. 

Muchas gracias Antonio es  una explicación excelente, desde luego no se me había ocurrido, tengo que hacer más ejercicios de este tipo para llegar a comprenderlo al 100%.

f`(x)= 3x^2+2ax+b              f`(4)=0  --> 48+8a+b=0  -->   b=-24

f``(x)=6x+2a                        f``(1)=0  -->  6+2a=0  ----->   a=-3

1)

Plantea las expresiones de las derivadas primera y segunda:

f ' (x) = 3x² + 2ax + b,

f ' ' (x) = 6x + 2a.

Luego, plantea la condición de punto crítico (posible extremo relativo) y la condición de punto de inflexión en los puntos indicados:

f ' (4) = 0,

f ' ' (1) = 0;

luego, sustituyes expresiones evaluadas en los primeros miembros de ambas ecuaciones, y queda:

48 + 8a + b = 0,

6 + 2a = 0;

luego, resuelves el sistema (te dejo la tarea), y queda: a = -3, b = -24.

Luego, la expresión de la función queda:

f(x) = x³ - 3x² - 24x;

y la expresión de su derivada primera queda:

f ' (x) = 3x² - 6x - 24 (observa que x = 4 es una de sus raíces);

y la expresión de su derivada segunda queda:

f ' ' (x) = 6x - 6 (observa que x = 1 es su raíz, y que f ' ' (4) = 18 > 0).

Espero haberte ayudado.

2)

Observa que el dominio de la función es R.

Luego, plantea la expresión de la función derivada primera:

f ' (x) = ( 3x²(3x²+1) - x³(6x) )/(3x²+1)² = (9x⁴+3x²-6x⁴)/(3x²+1)² = (3x⁴+3x²)/(3x²+1)² = 3x²(x²+1)/(3x²+1)².

Luego, plantea la condición de punto crítico (posible máximo o posible mínimo):

f ' (x) = 0, sustituyes en el primer miembro, y queda:

3x²(x²+1)/(3x²+1)² = 0, haces pasaje de divisor (observa que es estrictamente positivo) como factor, y queda:

3x²(x²+1) = 0, haces pasajes de factores estrictamente positivos como divisores, y queda:

x² = 0, haces pasaje de potencia como raíz, y queda:

x = 0.

Luego, observa que la expresión de la función derivada es positiva (su numerador es un producto de factores positivos, y su denominador es estrictamente positivo), por lo que tienes que la función derivada primera toma valores positivos en los intervalos: (-∞,0) y (0,+∞), por lo que la gráfica de a función es creciente en ambos intervalos y, por lo tanto, tienes que la función no presenta extremos, ya que es creciente en R - {0}.

Espero haberte ayudado.

muchisimas gracias!!

2)

Tienes el número complejo:

z = (4+2ni)/(3-i), multiplicas al numerador y al denominador por el conjugado del denominador, y queda:

z = (4+2ni)(3+i) / (3-i)(3+i) = (12+4i+6ni-2n)/(9+1) = ( (12-2n)+(4+6n)i )/10 = (12-2n)/10 + ( (4+6n)/10 )i.

a)

Plantea que la parte imaginaria es igual a cero:

(4 + 6n)/10 = 0, haces pasaje de divisor como factor, y queda:

4 + 6n = 0, haces pasaje de término, y queda:

6n = -4, haces pasaje de factor como divisor, y queda:

n = -2/3;

y la expresión del número complejo queda:

z = ( 4-(4/3)i )/(3-i) = 4/3 + 0i.

b)

Plantea que la parte real es igual a cero:

(12 - 2n)/10 = 0, haces pasaje de divisor como factor, y queda:

12 - 2n = 0, haces pasaje de término, y queda:

-2n = -12, haces pasaje de factor como divisor, y queda:

n = 6;

y la expresión del número complejo queda:

z = (4-12i)/(3-i) = 0 + 4i.

c)

Tienes el valor del módulo del número complejo:

|z| = √(2), sustituyes en el primer miembro por la expresión del módulo en función de las partes real e imaginaria, y queda:

√( ( (12-2n)/10 )² + ( (4+6n)/10 )² ) = √(2), elevas al cuadrado en ambos miembros, y queda:

( (12-2n)/10 )² + ( (4+6n)/10 )² = 2, distribuyes las potencias en los términos del primer miembro, y queda:

(12 - 2n)²/100 + (4 + 6n)²/100 = 2, multiplicas por 100 en todos los términos de la ecuación, y queda:

(12 - 2n)² + (4 + 6n)² = 200, desarrollas los binomios elevados al cuadrado, y queda:

144 - 48n + 4n² + 16 + 48n + 36n² = 200, reduces términos semejantes (observa que tienes cancelaciones), y queda:

40n² + 160 = 200, haces pasaje de término, y queda:

40n² = 40, haces pasaje de factor como divisor, y queda:

n² = 1, haces pasaje de potencia como raíz, y tienes dos opciones:

1°)

n = -1, y el número complejo queda: z = (4-2i)/(3-i) = 7/5 - (1/5)i;

2°)

n = 1, y el número complejo queda: z = (4-2i)/(3-i) = 1 + i.

Espero haberte ayudado.

4)

Plantea las expresiones de los números complejos en forma polar:

z = |z|_α,

w = |w|_β.

Luego, tienes en tu enunciado:

a)

z/w = 5, expresas a todos los números en forma polar, y queda:

|z|_α / |w|_β = 5_0°, resuelves en el primer miembro, y queda:

(|z|/|w|)_α-β = 5_0°, 

luego, comparas módulos, comparas argumentos, y quedan las ecuaciones:

|z|/|w| = 5, aquí haces pasaje de divisor como factor, y queda: |z| = 5*|w| (1),

α - β = 0°, aquí haces pasaje de término, y queda: α = β (2);

b)

α + β = 120° (3);

c)

|z| + |w| = 24 (4).

Luego, sustituyes la expresión señalada (1) en la ecuación señalada (4), y queda:

6*|w| = 24, aquí haces pasaje de factor como divisor, y queda: |w| = 4,

luego reemplazas en la ecuación señalada (1) y queda: |z| = 20.

Luego, sustituyes la expresión señalada (2) en la ecuación señalada (3), y queda:

2*β = 120°, aquí haces pasaje de factor como divisor, y queda: β = 60°,

luego reemplazas en la ecuación señalada (2), y queda: α = 60°.

Luego, la solución del problema, con los números complejos expresados en forma polar, queda:

z = 20_60°,

w = 4_60°.

Espero haberte ayudado.

¿Qué dice el enunciado del ejercicio, Bruno?

Si tienes que verificar que la función vectorial T es una transformación lineal, comienza por definir dos elementos del dominio (R³):

u = <a,b,c>, cuyo transformado queda: T(u) = <a,b-c,b+c>, y

v = <d,e,f>, cuyo transformado queda: T(v) = <d,d-e,d+e>,

y un número real genérico k.

1°)

T(u+v) = T(<a,b,c>+<d,e,f>) = T(a+d,b+e,c+f) = aplicas la transformación:

= <a+d,a+d-(b+e),b+e+c+f> = <a+d,a+d-b-e,b+e+c+f> = ordenas y asocias términos en las dos últimas componentes:

= <a+d,(a-b)+(d-e),(b+c)+(e+f)> = descompones como suma de dos vectores:

= <a,a-b,b+c> + <d,d-e,e+f> = T(u) + T(v).

2°)

T(k*u) = T(k*<a,b,c>) = T(ka,kb,kc) = aplicas la transformación:

= <ka,ka-kb,kb+kc> = extraes factores comunes en las dos últimas componentes:

= <ka,k(a-b),k(b+c)> = extraes el factor escalar:

= k*<a,a-b,b+c> = k*T(u).

Espero haberte ayudado.