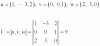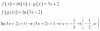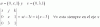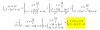-
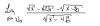 Como resuelvo sin l'hopital? Se que abajo hay una diferencia de cuadrado y se que que sale un (x-2b) que se me va a cancelar con algo del numerador, pero nose como arreglar arriba para que aparezca eso x.x
Como resuelvo sin l'hopital? Se que abajo hay una diferencia de cuadrado y se que que sale un (x-2b) que se me va a cancelar con algo del numerador, pero nose como arreglar arriba para que aparezca eso x.xAntonio Silvio Palmitano
el 2/12/17Separas en dos términos, y la expresión de la función queda:
f(x) = ( √(x)-√(2b) )/√(x2-4b2) - √(x-2b)/√(x2-4b2) = f1(x) - f2(x).
Luego, considera cada término por separado:
1)
f1(x) = ( √(x)-√(2b) )/√(x2-4b2) =
multiplicas al numerador y al denominador por la expresión "conjugada" del numerador:
= ( √(x)-√(2b) )( √(x)+√(2b) ) / √(x2-4b2)( √(x)+√(2b) ) = distribuyes en el numerador (observa que tienes cancelaciones):
= (x-2b) / √(x2-4b2)( √(x)+√(2b) ) = factorizas y distribuyes la raíz en el primer factor del denominador, y queda:
= (x-2b) / √(x-2b)√(x+2b)( √(x)+√(2b) ) = simplificas el numerador con el primer factor del denominador, y queda:
= √(x-2b) / √(x+2b)( √(x)+√(2b) ),
luego, plantea el límite para x tendiendo a 2b:
L1 = Lím(x→2b) f1(x) = Lím(x→2b) √(x-2b) / √(x+2b)( √(x)+√(2b) ) = 0 / √(4b)(2√(2b)) = 0.
2)
f2(x) = √(x-2b)/√(x2-4b2) = factorizas el argumento y distribuyes la raíz en el denominador, y queda:
= √(x-2b) / √(x-2b)√(x+2b) = simplificas el numerador con el primer factor del denominador, y queda:
= 1 / √(x+2b),
luego, plantea el límite para x tendiendo a 2b:
L2 = Lím(x→2b) f2(x) = Lím(x→2b) 1 / √(x+2b) = 1/√(4b).
Luego, como tienes que los límites de los términos existen, tienes para el límite de tu enunciado:
L = Lím(x→2b) f(x) = L1 - L2 = 0 - 1/√(4b) = -1/√(4b) = -1/( 2√(b) ).
Espero haberte ayudado.
-
Buenos días.
Me podrían ayudar con este ejercicio por favor.
Si f(x)=ln(x) y g(x)=3x+2 , entonces el conjunto de positividad de h=FoG es igual a:
͏͏Ο(-1/3 ; +∞)
͏͏Ο(1 ; +∞)
Ο(0 ; +∞)
Ο(-2/3 ; +∞)
Desde ya muchas gracias
Antonio Silvio Palmitano
el 2/12/17Observa que la primera función (g) tiene dominio R.
Observa que la segunda función (f) tiene dominio (0,+∞) = {x ∈ R / x > 0}.
Luego, recuerda las dos condiciones necesarias que debe cumplir un elemento del dominio de la función compuesta, para la existencia de la función g compuesta con f:
1°)
x ∈ Dg (observa que el dominio de la función g no impone restricciones);
2°)
g(x) ∈ Df, y como el dominio de la función f si impone condición, plantea:
g(x) > 0, sustituyes la expresión de la función en el primer miembro, y queda:
3x + 2 > 0, haces pasaje de término, y queda:
3x > -2, haces pasaje de factor como divisor, y queda:
x > - 2/3,
de donde tienes que el dominio de la función compuesta queda:
Dfog = (-2/3,+∞) = {x ∈ R / x > -2/3}.
Luego, plantea la expresión de la función compuesta g con f:
(f o g)(x) = f( g(x) ) = sustituyes la expresión de la primera función, y queda:
= f(3x+2) =
= ln(3x+2).
Luego, plantea la condición de postividad:
(f o g)(x) > 0, sustituyes la expresión de la función compuesta, y queda:
ln(3x+2) > 0, compones en ambos miembros con la función exponencial natural (observa que es una función creciente), y queda:
3x + 2 > 1, haces pasaje de término, y queda:
3x > -1, haces pasaje de factor como divisor, y queda:
x > -1/3,
por lo que puedes concluir que el intervalo de positividad de la función compuesta es:
(-1/3,+∞),
por lo que tienes que la primera opción es la respuesta correcta.
Espero haberte ayudado.
-
Considera los vectores u=(1,1,-3), v=(a,2,4) y w=(0,b,3). Calcula a y b sabiendo que u es perpendicular a v y v es perpendicular a w. Muchas gracias
Antonio Silvio Palmitano
el 2/12/17Vamos con una orientación.
Recuerda que si dos vectores no nulos son perpendiculares tienes que su producto escalar es igual a cero.
Luego, plantea:
u•v = 0, sustituyes las expresiones de los vectores, y queda:
<1,1,-3>•<a,2,4> = 0, desarrollas el producto escalar, y queda la ecuación:
1*a + 1*2 - 3*4 = 0, resuelves términos numéricos, reduces términos semejantes, haces pasaje de términos, y queda:
a = 10.
Luego, plantea:
v•w = 0, sustituyes las expresiones de los vectores (observa que ya tienes el valor de la incógnita a), y queda:
<10,2,4>•<0,b,3> = 0, desarrollas el producto escalar, y queda la ecuación:
10*0 + 2*b + 4*3 = 0, resuelves términos numéricos, reduces términos semejantes, haces pasaje de términos, y queda:
b = -6.
Espero haberte ayudado.
-
Buenas , no se resolver este sistema de ecuaciones.
xy=12
x2-5 y2=16
Antonio Silvio Palmitano
el 2/12/17Observa que x e y deben ser distintos de cero, para que la primera ecuación tenga sentido.
Luego, haces pasaje de factor como divisor en la primera ecuación, y queda:
y = 12/x (1).
Luego, sustituyes la expresión señalada (1) en la segunda ecuación, y queda:
x2 - 5(12/x)2 = 16, resuelves la potencia, y luego el coeficiente en el segundo término, y queda:
x2 - 720/x2 = 16, multiplicas por x2 en todos los términos de la ecuación (recuerda que x es distinto de cero), y queda:
x4 - 720 = 16x2, haces pasaje de término, y queda:
x4 - 16x2 - 720 = 0 (1);
luego, plantea la sustitución (cambio de incógnita):
x2 = w (2) (observa que w toma valores estrictamente positivos),
luego, sustituyes en la ecuación señalada (2), y queda:
w2 - 16w - 720 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:
a)
w = -20, que no es una solución válida para este problema (recuerda que w toma valores estrictamente positivos),
b)
w = 36, que si es una solución válida para este problema,
luego, reemplazas en la ecuación señalada (2), y queda:
x2 = 36, haces pasaje de potencia como raíz, y tienes dos opciones:
b1)
x = -6, luego reemplazas en la ecuación señalada (1), y queda: y = -2, por lo que tienes el punto A1(-6,-2),
b2)
x = 6, luego reemplazas en la ecuación señalada (1), y queda: y = 2, por lo que tienes el punto A2(6,2).
Espero haberte ayudado.
-
Buenos días, ¿podrían ayudarme con un problema? Envío el enunciado y hasta donde he llegado. Gracias.
Antonio Silvio Palmitano
el 2/12/17Vas muy bien.
Has estudiado la continuidad de la función en el punto de corte (x = 1), y tienes la ecuación:
m = a + b + 1 (1).
Has planteado correctamente la expresión de la función derivada:
f ' (x) =
m si x < 1
a determinar si x = 1
2ax + b si x > 1;
has planteado correctamente los limites laterales de la función derivada para x tendiendo a 1, que son: m (por izquierda) y 2a+b (por derecha),
luego, plantea la igualdad entre los límites laterales, y tienes la ecuación:
m = 2a + b (2).
Luego, plantea la condición de punto crítico (posible máximo o posible mínimo) para x = 3:
f ' (3) = 0,
luego, sustituyes la expresión de la función derivada evaluada en el primer miembro (observa que corresponde al segundo trozo), y queda:
6a + b = 0 (3).
Luego, sustituyes la expresión señalada (2) en la ecuación señalada (1), y queda:
2a + b = a + b + 1, haces pasajes de términos (observa que tienes cancelaciones), y queda: a = 1;
luego, reemplazas en la ecuación señalada (3), haces pasaje de término, y queda: b = -6;
luego, reemplazas en la ecuación señalada (1), resuelves y queda: m = -4.
Luego, la expresión de la función, cuyo dominio es R, queda:
f(x) =
-4x si x < 1
x2 - 6x + 1 si x ≥ 1,
y observa que la función es continua en x = 1.
Luego, la expresión de la función derivada primera queda:
f ' (x) =
-4 si x < 1
-4 si x = 1
2x-6 si x > 1,
y observa que está definida en R, y observa que x = 3 es un punto crítico de la función.
Luego, plantea la expresión de la función derivada segunda:
f ' ' (x) =
0 si x < 1
no está definida si x = 1
2 si x > 1,
y observa que está definida en R-{1}, y que es positiva en el punto crítico, por lo que la gráfica de la función es cóncava hacia arriba en el punto crítico x = 3, por lo que tienes que la función alcanza un mínimo relativo en dicho punto.
Espero haberte ayudado.
-
Si hace tres años la edad de Luis era el triple de la edad de Ana, y en siete años será el doble. ¿Cuál era la edad de Luis hace tres años?
Antonio Silvio Palmitano
el 2/12/17Puedes llamar x a la edad de Luís hace tres años (observa que su edad actual es: x+3, y que su edad dentro de siete años será: x+10).
Puedes llamar y a la edad de Ana hace tres años (observa que su edad actual es: y+3, y que su edad dentro de siete años será: y+10).
Luego, plantea la relación entre las edades de las personas hace tres años:
x = 3y (1).
Luego, plantea la relación entre las edades de las personas dentro de siete años:
x+10 = 2(y+10), aquí distribuyes, y queda: x+10 = 2y+20, haces pasajes de términos, y queda:
x - 2y = 10 (2).
Luego, sustituyes la expresión señalada (1) en la ecuación señalada (2), y queda:
3y - 2y = 10, reduces términos semejantes, y queda:
y = 10 años.
Luego, reemplazas en la ecuación señalada (1) y queda:
x = 30 años.
Observa que la edad de Luis hace tres años era 30 años, su edad actual es 33 años, y su edad dentro de siete años será 40 años.
Observa que la edad de Ana hace tres años era 10 años, su edad actual es 13 años, y su edad dentro de siete años será 20 años.
Espero haberte ayudado.
-
yo denuevo.
por favor denme como sus tips o sus formulas para la aplicacion de derivadas y en que casos utilizan cada formula porfavoor
Ángel
el 2/12/17Lamento decirte que no hay ninguna "piedra filosofal"...lo único que tienen en común los ejercicios de aplicación de derivadas es que tendrás que hacer primeras, segundas y hasta terceras derivadas; pero tienes que practicar con multitud de ejercicios tipo para ver cuando/cómo tienes que cálcular el máximo, mínimo (optimización), funciones tangentes y normal, crecimiento, curvatura, l´hopital y las condiciones a las que tienes que ceñirte en cada problema...
-
Muy buenas para todos.
Primera ves que me comunico con ustedes.
Les mando unas fotos de ejercicios y si pueden resolverlo si no fuera molestia.
Fueron realizado para un examen que tuvimos.
Desde ya agradezco las respuestas,
Saludos.