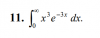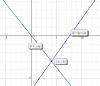
Tienes que el punto P(x,y) pertenece al tercer cuadrante, por lo que tienes que x es negativo e y es negativo.

Tienes que el punto P(x,y) pertenece a la recta bisectriz del primero y del tercer cuadrante, cuya ecuación cartesiana explícita es: y = x, por lo tanto, tienes que el punto queda expresado en la forma: P(x,x), con x negativo.

I)

Observa que esta proposición es Falsa, porque tienes que x es negativo y, por lo tanto, su opuesto (-x) es positivo.

II)

Observa que esta proposición es Falsa, porque la distancia entre el punto P(x,x) y el origen O(0,0) se expresa con una cantidad positiva, y tienes en este caso que x es negativa.

III)

Observa que esta proposición es Verdadera, porque el punto proyección pertenece al eje OY, y su abscisa es 0 y su ordenada es igual a la del punto P(x,x), por lo tanto la expresión del punto proyección es: Q(0,x).

IV)

Observa que esta proposición es Falsa, porque el punto proyección pertenece al eje OX, y su abscisa es igual a la del punto P(x,x) y su ordenada es 0, por lo tanto la expresión correcta del punto proyección es: A(x,0).

Luego, tienes que la opción B es la respuesta correcta.

Tienes los vectores horizontales (observa que consideramos sentido positivo hacia la derecha), de los que conoces sus módulos y sentidos, y plantemos su expresión en función de sus componentes:

A, hacia la izquierda, |A| = 10, por lo que su expresión es: A = <-10,0>;

B, hacia la derecha, |B| = 15, por lo que su expresión es: B = <15,0> (observa que tienes anotaciones incorrectas);

C, hacia la izquierda, |C| = 20, por lo que su expresión es: C = <-20,0> (observa que tienes anotaciones incorrectas).

Luego, plantea:

R = A - B - C = <-10,0> - <15,0> - <-20,0> = <-10-15-(-20),0-0-0> = <-10-15+20,0> = <-15,0>,

por lo que tienes que el vector resultante R tiene módulo |A-B-C| = 15 y apunta hacia la izquierda.

Por favor, consulta con tus docentes por las dudas se haya deslizado un error de imprenta en el enunciado.

Espero haberte ayudado.

Obtenemos la equis:

3x= -4y ----->  x=(-4/3)y

Sustituimos la equis obtenida anteriormente en la segunda ecuación (sustitución) para hallar el valor numérico de y :

5x - 6y = 38  ----> 5*(-4/3)y -6y=38  ----->  (-20/3)y -6y=38  ---->  (-38/3)y=38    ----> y= -3

Sustituimos y= -3 en la otra ecuación para hallar la primera coordenada del punto de intersección de las rectas, es decir, la x:

3x= -4y   ----> 3x=-4*(-3)  ---> x=4

x=4 , y= -3  ------> Punto de intersección de las rectas (x,y)=(4,-3)

Gráficamente:

∫4(cosx-1)dx=

4*∫(cosx-1)dx=

4*(∫cosx dx - ∫1 dx)=

4*(senx - x) + C =

4senx-4x+C

Gracias Crack!

Puedes plantear que el camino es recto, y que pasa por el origen de coordenadas y por un punto A(x,y) perteneciente a la frontera, por lo que su ecuación es:

y = mx (1),

luego, sustituyes la expresión señalada (1) en la ecuación de la frontera, y queda:

5x² + 6x*mx + 5(mx)² = 8, resuelves el segundo y el tercer término, y queda:

5x² + 6mx² + 5m²x² = 8, extraes factor común en el primer miembro, y queda:

x²(5 + 6m + 5m²) = 8, haces pasaje de factor como divisor, y queda:

x² = 8/(5 + 6m + 5m²) (2) .

Luego, plantea la expresión de la función "distancia cadrática" entre el origen y el punto A(x,y) de la frontera:

f(x,y) = d(P,A)² = ( √( (x-0)² + (y-0)² ) )² = ( √(x² + y² ) )² = x² + y²,

luego, sustituyes la expresión señalada (1) en la expresión de la función (a fin de reducir la cantidad de variables), y queda:

f(x) = x² + (mx)², resuelves el segundo término, extraes factor común, y queda:

f(x) = (1+m²)x², 

luego, sustituyes la expresión señalada (2) en la expresión de la función, y queda:

f(m) = 8(1+m²)/(5 + 6m + 5m²) (3).

Luego, plantea la expresión de la función derivada primera:

f ' (m) = 8( 2m(5 + 6m + 5m²) - (1+m²)(6+10m) ) / (5 + 6m + 5m²)²,

luego, plantea la condición de punto crítico (posible máximo o posible mínimo):

f ' (m) = 0, sustituyes en el primer miembro, y queda:

8( 2m(5 + 6m + 5m²) - (1+m²)(6+10m) ) / (5 + 6m + 5m²)² = 0,

haces pasaje de factor numérico como divisor, y de divisor como factor, y queda:

2m(5 + 6m + 5m²) - (1+m²)(6+10m) = 0, distribuyes en ambos términos, y queda:

10m + 12m² + 10m³ - 6 - 10m - 6m² - 10m³ = 0,

reduces términos semejantes (observa que tienes cancelaciones), ordenas términos, y queda:

6m² - 6 = 0, divides en todos los términos de la ecuación por 6, haces pasaje de término, y queda:

m² = 1, haces pasaje de potencia como raíz, y tienes dos opciones:

a)

m = -1, luego reemplazas en la ecuación señalada (2), y queda:

x² = 2, de donde tienes dos opciones:

a₁)

x = -√(2), que al reemplazar los valores remarcados en la ecuación señalada (1) queda: y = √(2),

por lo que tienes el punto A₁( -√(2) , √(2) ), que pertenece a la frontera y su distancia al origen es: D₁ = 2;

a₂)

x = √(2), que al reemplazar los valores remarcados en la ecuación señalada (1) queda: y = -√(2),

por lo que tienes el punto A₁( √(2) , -√(2) ), que pertenece a la frontera y su distancia al origen es: D₂ = 2.

b)

m = 1, luego reemplazas en la ecuación señalada (2), y queda:

x² = 1/2, de donde tienes dos opciones:

b₁)

x = -1/√(2), que al reemplazar los valores remarcados en la ecuación señalada (1) queda: y = -1/√(2),

por lo que tienes el punto B₁( -1/√(2) , -1/√(2) ), que pertenece a la frontera y su distancia al origen es: d₁ = 1;

b₂)

x = 1/√(2), que al reemplazar los valores remarcados en la ecuación señalada (1) queda: y = 1/√(2),

por lo que tienes el punto B₂( 1/√(2) , 1/√(2) ), que pertenece a la frontera y su distancia al origen es: d₂ = 1.

Luego, tienes que las trayectorias que minimizan la longitud del camino son las que unen al origen con los puntos B₁ y B₂.

Espero haberte ayudado.

https://es.symbolab.com/solver/step-by-step/%5Cint_%7B0%7D%5E%7B1%7D%20%5Cleft(%5Cfrac%7B1%7D%7B%5Csqrt%7B-3lnx%7D%7D%5Cright)dx

Algún método en particular ? 
En funciones de ese tipo si bien es cierto que se puede obtener por partes , es más sencillo si se trabaja con el método tabular
Ver el siguiente video https://www.youtube.com/watch?v=TpkldNa011c
En todo caso indicas para poder colaborarte.

https://es.symbolab.com/solver/step-by-step/%5Cint_%7B0%7D%5E%7B%5Cinfty%7D%20%5Cleft(x%5E%7B3%7De%5E%7B-3x%7D%5Cright)dx

Matriz de Cambio de Base 01 Matriz de Cambio de Base 02

Puedes llamar x al precio de compra de una decena de petates,

por lo que tienes que x+3 es el precio de venta (observa que x es estrictamente positivo).

Puedes llamar n a la cantidad de decenas de petates que ha comprado el comerciante

y observa también que n es un número natural.

Luego, tienes para la compra:

n*x = 60 (1),

Luego, tienes para la venta:

(n-3)*(x+3) = 63 (2)

y observa que la ganancia es 63 - 3 = 3 unidades monetarias.

Luego, haces pasaje de factor como divisor en la ecuación señalada (1), y queda:

n = 60/x (3);

luego, sustituyes la expresión señalada (3) en la ecuación señalada (2), y queda:

(60/x - 3)*(x + 3 ) = 63, distribuyes en el primer miembro, y queda

60 + 180/x - 3x - 9 = 63, multiplicas por x en todos los términos de la ecuación, y queda:

60x + 180 - 3x² - 9x = 63x, haces pasaje de término, reduces términos semejantes, ordenas términos, y queda:

-3x² -12x + 180 = 0, divides en todos los términos de la ecuación por -3, y queda:

x² + 4x - 60 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:

a)

x = -10, que no tiene sentido para este problema (recuerda que x toma valores estrictamente positivos);

b)

x = 6 unidades monetarias, que si tiene sentido para este problema;

luego, reemplazas en la ecuación señalada (3) y tienes:

n = 60/6 = 10 decenas de petates.

Espero haberte ayudado.

La z puede tomar infinitos valores...

x= (7-z)/7    

y= (14+11z)/7

z=z