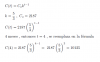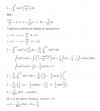Muéstranos tu trabajo.

Estos son muy sencillos y directos , tómese su tiempo de leerlo con calma inténtelo . 
Lo único que debe hacer acá es reemplazar el valor que le dan en la fórmula dada. Example en el primero reemplaza en la fórmula t=0 y después t=10
En el segundo t = 8 en la fórmula que allí le indican . Use una calculadora .

1)

La respuesta correcta es 5, ya que: 3⁵ = 3*3*3*3*3 = 243.

2)

Tienes la ecuación:

P₀*(1 + i)ⁿ = P₀*e^0,03*n, haces pasaje de factor (P₀) como divisor, simplificas, y queda:

(1 + i)ⁿ = e^0,03*n, haces pasaje de potencia como raíz, y queda:

1 + i = ⁿ√(e^0,03*n), simplificas el índice de la raíz con el exponente de la potencia en el segundo miembro, y queda:

1 + i = e^0,03, haces pasaje de término, y queda:

i = e^0,03 - 1.

Espero haberte ayudado.

Función exponencial

Acá también veo errores .
- La población para t=0 debe dar 500 000 esto es 500 mil  , allí le falta un cero a la fórmula ya que sólo pone 50000 que es  50 mil
- Siendo t un positivo entonces 0.05*t va ser positivo , luego la función es creciente , osea que la población va aumentar con los años , lo cual no debe ser así ya que       dice que disminuye .
- Por último haciendo las correcciones respectivas y evaluando para t=10 tampoco se obtiene una de las claves allí mostradas .
No sé de donde estás sacando esos ejercicios .

Debes "completar un binomio elevado al cuadrado" en la expresión de la función.

Tienes:

h(t) = -5*t² + 40*t, extraes factor común (-5), y queda:

h(t) = -5*(t² - 8*t), sumas y restas 16 en el agrupamiento, y queda:

h(t) = -5*(t² - 8*t + 16 - 16), factorizas el trinomio cuadrado perfecto, y queda:

h(t) = -5*( (t - 4)² - 16), distribuyes el factor común (-5), y queda:

h(t) = -5*(t - 4)² - 80,

luego, observa que la gráfica de la función tiene la ecuación:

y = -5*(t - 4)² + 80,

que es la ecuación canónica de una parábola, cuyo vértice es el punto V(4,80),

que es el punto "más alto" de la gráfica de la parábola,

por lo que tienes que el móvil alcanza en el instante t = 4 s, su altura máxima: h(4) = 80 m.

Espero haberte ayudado.

Es que eso no es una ecuación porque no está igualado a ninguna otra expresión , no aparece el igual  ( = )
Parece que tus problemas tienen un " problema " y es que están mal editados.

No. En un espacio vectorial siempre ha de estar el vector nulo.