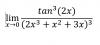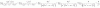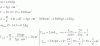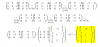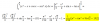-
Antonius Benedictus
el 27/11/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Antonio Silvio Palmitano
el 27/11/17Tienes que los coeficientes a, b son distintos de cero.
Luego, tienes los casos:
1)
a > 0, lo que conlleva: b > 0, ya que tienes una igualdad entre una suma de términos positivos en el primer miembro;
y luego tienes dos opciones:
1a)
a = 1, y tienes una familia de circunferencias con centro (0,0) y radio R = √(b), cuya ecuación es: x2 + y2 = b,
por ejemplo, para b = 4 queda: x2 + y2 = 4;
1b)
a ≠ 1, y tienes una familia de elipses con centro de simetría (0,0), y aquí tienes otras dos opciones:
1b1)
a < 1, y tienes una familia de elipses con eje focal OX, cuya ecuación es: ax2 + y2 = b,
por ejemplo, para a = (1/4) y b = 1 queda: x2/4 + y2 = 1;
1b2)
a > 1, y tienes una familia de elipses con eje focal OY, cuya ecuación es: ax2 + y2 = b,
por ejemplo, para a = 4 y b = 4 queda: 4x2 + y2 = 4,
luego divides en todos los términos de la ecuación por 4 y queda: x2 + y2/4 = 1.
2)
a < 0, a partir de la cuál tienes dos opciones:
2a)
b > 0, y tienes una familia de hipérbolas con centro de simetría (0,0) y eje focal OY, cuya ecuación es: ax2 + y2 = b,
por ejemplo, para a = -1 y b = 1 queda: -x2 + y2 = 1;
2b)
b < 0, y tienes una familia de hipérbolas con centro de simetría (0,0) y eje focal OX, cuya ecuación es: ax2 + y2 = b,
por ejemplo, para a = -1 y b = -1 queda: -x2 + y2 = -1,
luego multiplicas en todos los términos de la ecuación por -1 y queda: x2 - y2 = 1.
Espero haberte ayudado.
-
¿Alguien me ayuda a hacer cambio de coordenadas de esta integral? ya sea a cilíndricas o esféricas, por favor.
Antonius Benedictus
el 27/11/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Antonio Silvio Palmitano
el 27/11/17Tienes, a partir de los límites de integración para z:
z = 0 (plano coordenado OXY);
z = √(16-x2-y2) (semiesfera superior, con centro en el origen y radio 4).
Luego, plantea los límites para y (en el plano coordenado OXY):
y = 0 (eje coordenado OX);
y = √(4-x2) (semicircunferencia superior, con centro en el origen y radio 2).
Luego, tienes los limites para x:
x = 0,
x = 2.
Luego, observa que tienes el sólido en el primer octante, limitado inferiormente por el plano OXY, superiormente por la esfera con centro en el origen y radio 4, y lateralmente por un cilindro circular de eje OZ y radio 2.
Luego, puedes plantear el cambio a coordenadas cilíndricas, cuyo factor de compensacion (Jacobiano) es: |J| = r:
0 ≤ z ≤ √(16-r2)
0 ≤ r ≤ 2
0 ≤ θ ≤ π/2.
Luego, la integral queda:
I = ∫∫∫ √(x2+y2)*dx*dy*dz = ∫∫∫ √(r2)*r*dz*dr*dθ = ∫∫∫ r2*dz*dr*dθ = y puedes continuar la tarea.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 27/11/17Comienza por plantear la doble matriz
3 5 4 1 0 0
1 2 2 0 1 0
0 -1 1 0 0 1
Permutas la fila 1 con la fila 2, y queda:
1 2 2 0 1 0
3 5 4 1 0 0
0 -1 1 0 0 1
A la fila 2 le restas el triple de la fila 1, y queda:
1 2 2 0 1 0
0 -1 -2 1 -3 0
0 -1 1 0 0 1
A la fila 2 la multiplicas por -1, y queda:
1 2 2 0 1 0
0 1 2 -1 3 0
0 -1 1 0 0 1
A la fila 1 le restas el doble de la fila 2, a la fila 3 le sumas la fila 2, y queda:
1 0 -2 2 -5 0
0 1 2 -1 3 0
0 0 3 -1 3 1
A la fila 3 la multiplicas por 1/3, y queda:
1 0 -2 2 -5 0
0 1 2 -1 3 0
0 0 1 -1/3 1 1/3
A la fila 1 le sumas el doble de la fila 3, a la fila 2 le restas el doble de la fila 3, y queda:
1 0 0 4/3 -3 2/3
0 1 0 -1/3 1 -2/3
0 0 1 -1/3 1 1/3;
y tienes que la matriz A-1 tiene los elementos que hemos remarcado.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 27/11/17En este ejercicio no necesitas plantear cambio de variable, porque como bien has consignado en tu primera línea, tienes que el numerador del argumento del límite tiende a 1, y que su denominador tiende a cero, por lo que el límite es infinito.
Luego, si quieres determinar si el límite es -infinito o +infinito, ahí si puedes plantear el cambio de variable, pero, observa que has cometido un error al simplificar en tu última línea, porque el denominador de la expresión no puede simplificarse con el argumento del seno (recuerda que puedes simplificar factores comunes entre el numerador y el denominador de una expresión fraccionaria).
Por lo tanto, el límite queda:
Lím(t→0) cos(t2+6t) / t = ±∞;
observa, como hemos señalado, que el numerador tiende a 1 y que el denominador tiende a cero;
luego, plantea los límites laterales:
Lím(t→0-) cos(t2+6t) / t = -∞ (observa que el denominador tiende a 0 desde valores negativos);
Lím(t→0+) cos(t2+6t) / t = +∞ (observa que el denominador tiende a 0 desde valores positivos).
Espero haberte ayudado.