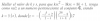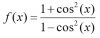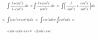-
Antonio Silvio Palmitano
el 17/9/17Tienes la expresión de la función:
y = √(2x+5) = (2x+5)1/2 (1).
Tienes las ecuación diferencial:
dx/dt = 12 (2).
Tienes también:
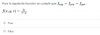
x0 = 24 (3),
y0 = a determinar,
dy/dt = a determinar.
Reemplazas el valor señalado (3) en la ecuación de la función señalada (1) y tienes:
y0 = √(2(24)+5) = √(48+5) = √(53).
Derivas con respecto a t en la ecuación señalada (1) (observa que debes aplicar la regla de la cadena) y queda:
dy/dt = (1/2)(2x+5)-1/2(2)(dx/dt) = (2x+5)-1/2(dx/dt),
luego reemplazas el valor señalado (3) y queda:
dy/dt = (53)-1/2(12) = 12/531/2 = 12/√(53) = 12V(53)/53.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 17/9/175)
Observa que las coordenadas del punto A(3,1) verifican la ecuación, por lo que tienes que dicho punto pertenece a la curva.
Comienza por derivar implícitamente con respecto a x y queda:
4(x2 + y2)( 2x + 2y*y ' ) = 50( 2x - 2y*y ' ),
luego reemplazas las coordenadas del punto A, resuelves términos en los agrupamientos, y queda:
4(10)( 6 + 2y ' ) = 50( 6 - 2y ' ),
distribuyes en ambos miembros y queda:
240 + 80y ' = 300 - 100y ',
haces pasajes de términos y queda:
180y ' = 60,
haces pasaje de factor como divisor y queda:
y ' = 1/3, que es la pendiente de la recta tangente;
luego, con las coordenadas del punto A puedes plantear la ecuación cartesiana de la recta tangente a la curva:
y - 1 = (1/3)(x - 3).
Espero haberte ayudado.
Antonio Silvio Palmitano
el 17/9/176)
Observa que tienes la pendiente de la recta tangente, por lo que puedes plantear: y ' = - 1 (1).
Luego, derivas implícitamente con respecto a x en la ecuación de la curva, y queda:
2x*y2 + x2*2y*y ' + 1*y + x*y ' = 0,
reemplazas el valor señalado (1) resuelves productos numéricos en los términos y queda:
2x*y2 - 2x2*y + y - x = 0,
extraes factores comunes por grupos de dos términos, y queda:
2xy*(y - x) + 1*(y - x) = 0,
extraes factor común y queda:
(y - x)*(2xy + 1) = 0,
luego, por anulación de un producto, tienes dos opciones:
a)
y - x = 0, aquí haces pasaje de término y queda:
y = x (2),
luego sustituyes en la ecuación de la curva, y queda:
x4 + x2 = 2,
aplicas la sustitución (cambio de incógnita): w = x2 (3) (observa que w toma valores positivos), haces pasaje de término y queda:
w2 + w - 2 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:
a1)
w = - 2, que no tiene sentido para este problema,
a2)
w = 1, que al sustituir en la ecuación señalada 3 queda:
x2 = 1, haces pasaje de potencia como raíz y tienes dos opciones:
1°)
x = - 1, reemplazas en la ecuación señalada (2) y queda: y = - 1, por lo que tienes el punto: A(-1,-1);
2°)
x = 1, reemplazas en la ecuación señalada (2) y queda: y = 1, por lo que tienes el punto: B(1,1);
y puedes verificar que las coordenadas de ambos puntos verifican la ecuación de la curva.
b)
2xy + 1 = 0 (observa que tanto x como y deben tomar valores distintos de cero), haces pasaje de término y queda:
2xy = - 1, haces pasajes de factores como divisores y queda:
y = - 1/(2x),
luego sustituyes en la ecuación de la curva y queda:
x2( -1/(2x) )2 + x( -1/(2x) ) = 2, resuelves en cada término y queda:
1/4 - 1/2 = 2, resuelves el primer miembro y queda:
- 1/4 = 2, que es una identidad absurda,
por lo que tienes que esta opción no conduce a puntos de contacto entre la curva y rectas tangentes con pendiente -1.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 17/9/177)
Observa que la pendiente de la recta tangente es -1, por lo que puedes plantear: y ' = -1 (1).
Luego derivas con respecto a x en la ecuación de la curva y queda:
y ' = 3x2 - 12x + 8,
luego igualas expresiones entre esta última ecuación y la ecuación señalada (1) y queda:
3x2 - 12x + 8 = - 1, haces pasaje de término y queda:
3x2 - 12x + 9 = 0, divides por 3 en todos los términos de la ecuación y queda:
x2 - 4x + 3 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:
a)
x = 1, luego reemplazas en la ecuación de la curva y queda:
y = (1)3 - 6(1)2 + 8(1) = 1 - 6 + 8 = 3,
por lo que tienes el punto: A(1,3)
que verifica la ecuación de la curva, pero observa que no verifica la ecuación de la recta tangente, por lo que no es un punto de tangencia;
b)
x = 3, luego reemplazas en la ecuación de la curva y queda:
y = (3)3 - 6(3)2 + 8(3) = 27 - 54 + 24 = -3,
por lo que tienes el punto: B(3,-3)
que verifica la ecuación de la curva y también de la recta tangente, por lo que si es un punto de tangencia.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 17/9/178)
Tienes la expresión de la función (observa que su dominio es el conjunto de los números reales):
f(x) = 2senx + sen2x,
luego derivas (observa que en el segundo término debes aplicar la regla de la cadena) y queda:
f ' (x) = 2cosx + 2senx*cosx,
luego, como tienes que las rectas tangentes son horizontales, tienes que sus pendientes son iguales a cero, y puedes plantear:
f ' (x) = 0, sustituyes la expresión de la función derivada y queda:
2cosx + 2senx*cosx = 0, divides por 2 en todos los términos de la ecuación y queda:
cosx + senx*cosx = 0, extraes factor común y queda:
cosx*(1 + senx) = 0,
luego, por anulación de un producto, tienes dos opciones:
a)
cosx = 0, compones con la función inversa del coseno y queda:
x = k*π, con k ∈ Z,
luego sustituyes en la expresión de la función y queda:
y = f(k*π) = 2sen(k*π) + sen2(k*π) = 2(0) + (0)2 = 0 + 0 = 0,
por lo que tienes los puntos de tangencia cuyas coordenadas son:
A(k*π,0), con k ∈ Z;
b)
1 + senx = 0, haces pasaje de término y queda:
senx = - 1, compones con la función inversa del seno y queda:
x = -π/2 + 2m*π, con m ∈ Z,
luego sustituyes en la expresión de la función y queda:
y = f(-π/2 + 2m*π) = 2sen(-π/2 + 2m*π) + sen2(-π/2 + 2m*π) = 2(-1) + (-1)2 = -2 + 1 = -1,
por lo que tienes los puntos de tangencia cuyas coordenadas son:
B(-π/2 + 2m*π,0), con m ∈ Z.
Espero haberte ayudado.
-
Exprese las cantidades dadas en función de sen x y cos x.
1. cos(π+x)
2. sen(2π-x)
Ángel
el 17/9/171.
cos(π+x)= -cosx
cos2x=1-sen2x
cosx= √(1-sen2x)
-cosx= -√(1-sen2x)= -√[1-(senx)2]
cos(π+x)= -cosx= -√[1-(senx)2]
---------------------------------------------------
2.
sen(2π-x)= sen(-x)= -senx
sen2x=1-cos2x
senx=√(1-cos2x)
-sen= -√(1-cos2x) = -√[1-(cosx)2]
sen(2π-x)= -senx= -√[1-(cosx)2]
-
David
el 27/9/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)